Anschauung zur Prozentrechnung 
Denken im 100er-Raster
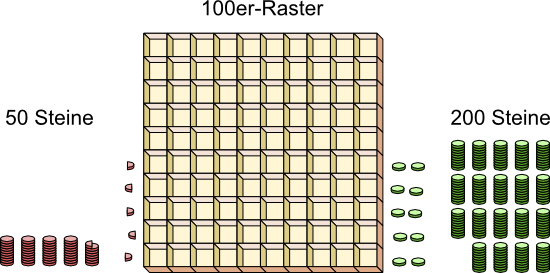
Aufgabe 1: Wer Prozentrechnung betreibt, denkt immer in einem 100er-Raster, in dem vorhandene Größen gleichmäßig aufgeteilt werden. 50 Steine werden z.B. so in dieses Gedankenraster sortiert, dass in jedem Kästchen ein halber Stein liegt. 200 Steine werden so gefächert, dass sich jeweils zwei in einem Kästchen befinden. Immer teilt man gedanklich etwas Ganzes in 100 gleich große Teile (Hundertstel) ein. Das wird gemacht, um unterschiedliche Größen gerecht miteinander vergleichen zu können. Erhält jemand beispielsweise von den 200 grünen Steinen 120, dann bekommt er im Gedanken den Inhalt aus 60 Kästchen (60 %). Wie viel rote Steine erhält er, wenn er von ihnen einen genauso großen Anteil (60 %) bekommen soll?
Antwort: Er erhält Steine.Versuche: 0
Aufgabe 2: Trage ein, wie viele Steine oder Teile eines Steines in jedes Kästchen kommen, wenn die angegebene Anzahl aller Steine gedanklich auf alle Kästchen im 100er-Raster gleichmäßig verteilt wird.
| Alle Steine | 20 | 40 | 60 | 300 | 400 | 550 | Grundwert |
| (Teil)-Steine je Kästchen | Prozentwert |
Versuche: 0
Aufgabe 3: Trage ein, wie viele Steine insgesamt in den 100 Kästchen des 100er-Rasters sind, wenn sich die aufgeführte Teilmenge in einem Kästchen befindet.
| Steine je Kästchen | 0,3 | 0,75 | 1,25 | 6 | 7,05 | 8,502 | Prozentwert |
| Alle Steine im 100er-Raster | Grundwert |
Versuche: 0
Aufgabe 4: Von der Anzahl aller Steine, die im 100er-Raster gleichmäßig auf Kästchen verteilt sind, wird eine vorgegebene Menge benötigt. Wie viele Kästchen müssen dafür entleert werden?
| Alle Steine | 100 | 200 | 300 | 400 | 500 | 600 | Grundwert |
| Benötigte Steine | 5 | 40 | 21 | 224 | 450 | 330 | Prozentwert |
| Anzahl der Kästchen | Prozentsatz |
Versuche: 0
Aufgabe 5: In großen Keksschachteln mit jeweils 100 Kästchen sind eine große Menge Kekse gleichmäßig verteilt. Für ein Fest wird eine unterschiedliche Anzahl von Keksen benötigt, um sie auf Tellern zu verteilen. Finde aus der folgenden Tabelle heraus:
a) Wie viele Kekse sich insgesamt in einer Hunderter-Box befanden.
b) Wie viele Kekse in einem Kästchen einer Hunderter-Box sind.
c) Wie viele Kekse beim Fest angeboten werden.
d) Aus wie vielen Kästchen der Hunderter-Box Kekse herausgeholt wurden.
| a) alle Kekse je 100er-Box (Grundwert) |
b) Kekse je Kästchen (1%) |
c) angebotene Kekse (Prozentwert) |
d) benötigte Kästchen (Prozentsatz) |
|
| Butterkekse | ||||
| Milchkekse | ||||
| Schokokekse |
richtig: 0falsch: 0
Grundbegriffe
Prozent bedeutet Hundertstel. Als Zeichen verwendet man %.
Teile ich ein Ganzes (200 Steine; 50 m ...) in Hundert gleich große Teile auf, dann entspricht eines dieser Teile (2 Steine; 0,5 m ...) einem Prozent: Einem Teil von Hundert ( 1 100 ). Das vorgegebene Ganze (200 Steine; 50 m ...) wird Grundwert genannt. Eine Teilmenge des Grundwertes wird als absoluter Prozentwert (2 Steine; 0,5 m ...) oder relativer Prozentsatz (1%) angegeben.
Aufgabe 6: Klick die richtigen Begriffe an.
- Prozentzeichen -
- Grundwert - das Ganze (s.o. alle Steine)
- Prozentwert - Teil des Ganzen (s.o. ein Teil der Steine)
- Prozentsatz - Teil des Ganzen (s.o. ein Teil der Kästchen)
Während Grund und Prozent immer gleichartige Einheiten (m - m, m - cm; kg - kg, kg - g; ...) haben, steht beim Prozent stets das Prozentzeichen ().
Versuche: 0
Aufgabe 7: Entscheide für die folgenden Texte, was der Grundwert ![]() , der Prozentwert
, der Prozentwert ![]() und der Prozentsatz
und der Prozentsatz ![]() ist. Klick dafür auf die Pfeile im Text und markiere die richtige Farbe.
ist. Klick dafür auf die Pfeile im Text und markiere die richtige Farbe.
| a) | Eine Buchhandlung verkauft 200 Bücher |
| b) | In einem Garten sind 120 m² |
| c) | Eine neue Straße ist zu 75 % |
Versuche: 0
Aufgabe 8: Klick auf die Zahlen und trage die gesuchten Begriffe ein.
|
Aufgabe 9 a: Beobachte bei der folgenden Animation, wie sich Grundwert, Prozentwert und Prozentsatz zueinander verhalten.
| Tempo: | ||||||||||||||||||||||||||||||||||||||||
Grundwert =  (100%) (100%)Das Ganze |
||||||||||||||||||||||||||||||||||||||||
Prozentwert A =  Absoluter Teil des Ganzen |
Prozentwert B = Absoluter Teil des Ganzen |
|||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
| Prozentsatz A = %
Relativer Teil des Ganzen |
Prozentsatz B = %
Relativer Teil des Ganzen |
|||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
Aufgabe 9 b: Markiere im Klappmenü "Tempo" (Aufgabe 9 a) den Begriff "schrittweise". Klick so lange in die Ausgabefelder der Smileys, bis die Vorgaben einer Tabellenzeile erreicht sind. Lies die übrigen Daten ab und trage sie in die entsprechenden Felder ein.
| Grundwert | Prozentwert A | Prozentsatz A | Prozentwert B | Prozentsatz B |
| 15 |
9 |
% | |
% |
| |
9 |
30 % | |
% |
| |
7 |
% | 13 |
% |
| |
18 |
75 % | |
% |
| 25 |
|
32 % | |
% |
Versuche: 0
Aufgabe 10:
| a) | Stelle mit Hilfe der orangen Punkte im Rechteck einen Grundwert von 20 cm2 ein. Lies die Prozentwerte und Prozentsätze für ¼, ½ und ¾ des Grundwertes ab und trage sie in die entsprechenden Stellen ein. |
| b) | Stelle mit Hilfe der orangen Punkte im Kreis einen Grundwert von 16 cm2 ein. Lies die Prozentwerte und Prozentsätze für ¼, ½ und ¾ des Grundwertes ab und trage sie in die entsprechenden Stellen ein. |
|
Rechteck Grundwert: 20 cm2 |
Kreis Grundwert: 16 cm2 |
||||||
| Bruch | 1/4 | 1/2 | 3/4 | 1/4 | 1/2 | 3/4 | |
| Prozentsatz | % | 50 % | % | % | % | % | |
| Prozentwert | cm2 | cm2 | cm2 | cm2 | cm2 | cm2 | |
Versuche: 0
Aufgabe 11: Gib 1% der Größe in der kleineren Einheit an.
| 100 % | 1 € | 10 € | 1 m | 100 m |
| 1 % | ct | ct | cm | cm |
| 100 % | 1 kg | 10 kg | 1 t | 0,5 t |
| 1 % | g | g | kg | kg |
Versuche: 0
Aufgabe 12: In der folgenden Grafik ist P der Prozentwert, G der Grundwert und p% der Prozentsatz. Stelle mit den orangen Schiebern die beiden vorhandenen Zeilenwerte der Tabelle ein. Lies den fehlenden Wert in der Grafik ab und trage ihn in die entsprechende Lücke ein.
| P | G | p% | |
| a) | € | 120 € | 50 % |
| b) | 84 € | 140 € | % |
| c) | 81 € | € | 45 % |
| d) | € | 200 € | 80 % |
| e) | 114 € | 150 € | % |
| f) | 80 € | € | 32 % |
Versuche: 0

