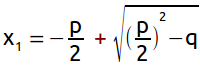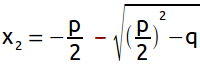Grundkenntnisse zur Abschlussprüfung der Werkrealschule (BW)
Die Grundkenntnisse aus Klasse 9 werden vorausgesetzt.
Die folgenden Aufgaben zeigen grundlegende Bereiche auf, die in der Abschlussprüfung auf dich zukommen. Versuche sie - soweit möglich - ohne Taschenrechner zu lösen.
Tipp: Konzentriere dich auf die Aufgabentypen, die du kannst und festige sie durch Üben. Bleib nicht zu lange an Aufgabentypen hängen, die dir größte Schwierigkeiten bereiten. Du musst nicht verzweifeln, um dich auf die Prüfung vorzubereiten. Verbessere das, was du in der Lage bist zu verbessern!
Potenzen
- Du kannst mit Potenzen rechnen.
Aufgabe 1: Ergänze die vereinfachten Terme richtig.
| a) |
| b) |
| c) |
| d) |
| e) |
| f) |
richtig: 0falsch: 0
Aufgabe 2: Trage die fehlenden Werte ein.
| a) | = | 1 | b) | = | |
| c) | 1 | = | d) | 1 | = |
| 2 | 2 |
richtig: 0falsch: 0
Exponentielles Wachstum
- Du kannst den Endwert (Wn), den Anfangswert (W0), die Wachstumsrate (p) und den Wachstumsfaktor (q) von exponentiellen Wachstumsprozessen berechnen.
Aufgabe 3: Trage die fehlenden Werte ein. Runde in den beiden linken Spalten auf Einer und in den beiden rechten auf zwei Nachkommastellen.
| Runde auf Einer. |
Runde auf Hundertstel. |
|||
| W0 | p | q | Wn | |
| a) | % | |||
| b) | % | |||
| c) | % | |||
| d) | % | |||
| e) | % | |||
| f) | % | |||
richtig: 0falsch: 0
Binomische Formeln
- Du kannst die Klammern von Binomen auflösen.
Aufgabe 4: Trage die fehlenden Werte ein.
|
a) (6 + x)² = + x + x² b) (y - 7)² = y² - y + c) ( + z) · ( - z) = 25 - z² |
richtig: 0falsch: 0
Aufgabe 5: Löse die Klammern schriftlich auf. Trage dann die richtigen Werte ein.
|
a) ()2 = a2 + a + b) ()2 = - b + b2 |
richtig: 0falsch: 0
Aufgabe 6: Löse die Klammern schriftlich auf. Trage dann die richtigen Werte ein.
|
|||||||||||||
|
richtig: 0falsch: 0
Lineare Gleichungssysteme
- Du kannst lineare Gleichungssysteme lösen.
Aufgabe 7: Löse das Gleichungssystem.
Lösung: (|)
richtig: 0falsch: 0
Aufgabe 8: Löse das Gleichungssystem.
Lösung: (|)
richtig: 0falsch: 0
Quadratische und gemischt quadratische Gleichungen
- Du kannst quadratische und gemischt quadratische Gleichungen lösen.
Aufgabe 9: Trage den positiven Wert von x1 ein. Der entsprechende negative Wert x2 wird automatisch angezeigt.
| a) x² = ; x1 = ; x2 = -zzz | |||||||||
| b) x² = ; x1 = ; x2 = -zzz | |||||||||
|
|||||||||
|
|||||||||
| f) -x² = ; x1 = ; x2 = -zzz |
richtig 0falsch 0
Aufgabe 10: Forme die Gleichung zuerst um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
| a) | x1 = | x2 = | b) | x1 = | x2 = |
| c) | x1 = | x2 = | d) | x1 = | x2 = |
| |||
Aufgabe 11: Löse die Klammer auf und trage die entsprechenden Beträge in die Textfelder unterhalb der Gleichung ein. Stelle die Gleichung anschließend in die Normalform um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
richtig: 0falsch: 0
Strahlensatz
- Du kannst mit Hilfe der Strahlensätze Streckenlängen in Dreiecken berechnen.
Aufgabe 12: Trage die Länge der Seite mit dem entsprechenden Buchstaben ein.
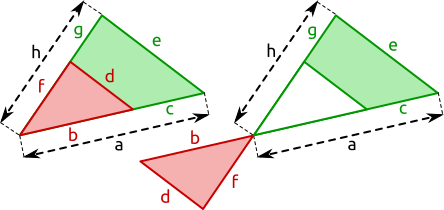
= cm
richtig: 0falsch: 0
Aufgabe 13: Trage die Länge der Seite mit dem entsprechenden Buchstaben ein.
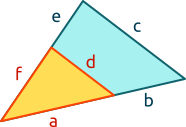
cm
richtig: 0falsch: 0
Trigonometrie
- Du kannst mit Hilfe der Trigonometrie Streckenlängen und Winkel in rechtwinkligen und allgemeinen Dreiecken berechnen.
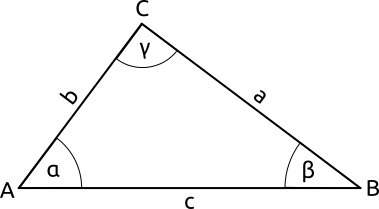
Aufgabe 14: Ein Dreieck hat die Winkel
Antwort: Die Seite ist cm lang. Kürze auf eine Stelle nach dem Komma.
richtig: 0falsch: 0
Aufgabe 15: Trage den gesuchten Winkel (α oder β) des rechtwinkligen Dreiecks mit γ = 90° ein. Runde auf ganze Gradangaben.
α = °
richtig: 0falsch: 0
Aufgabe 16: Die Entfernung zwischen zwei Leuchttürmen beträgt . Von Leuchtturm A ist das Schiff in einem Winkel von zu sehen. An Leuchtturm B beträgt der Winkel . Wie weit ist das Schiff von beiden Leuchttürmen entfernt? Trage die fehlenden ganzzahligen Werte ein.
Das Schiff ist von Leuchtturm A , km und von Leuchtturm B , km weit entfernt.
richtig: 0falsch: 0
Aufgabe 17: Die Skizze unten gibt an, wie weit zwei Türme von einem Aussichtspunkt entfernt sind und in welchem Winkel die Messstrecken zueinander stehen. Wie weit sind die beiden Türme voneinander entfernt? Runde auf ganze Kilometer.
Die zwei Türme stehen km voneinander entfernt.
richtig: 0falsch: 0
Zinseszins
- Du kannst Anfangs- und Endkapital sowie Zinsen, Zinssatz und Laufzeit von mehrjährigen Geldanlagen berechnen.
Aufgabe 18: Trage die fehlenden Werte ein. Am unteren Teil der Tabelle ist angegeben, auf wie viele Nachkommastellen das Ergebnis gerundet werden soll.
| Anfangs kapital |
Zins- satz |
Lauf -zeit |
Zinsen | End- kapital |
| € | € | |||
| € | € | |||
| % | € | |||
| % | € | |||
| Jahre | € | |||
| 0 | 1 | 0 | 2 | |
| ↑ Anzahl der einzutragenden Nachkommastellen ↑ | ||||
richtig: 0falsch: 0
Kugel
- Du kannst Kugeloberfläche und -volumen sowie Radius und Durchmesser berechnen.
Aufgabe 19: Klick das richtige Volumen und die richtige Oberfläche an.
|
a) Oberfläche = cm²
richtig: 0 | falsch: 0
|
||
|
b) Volumen = cm³
richtig: 0 | falsch: 0
|
||
Aufgabe 20: Trage die fehlenden ganzzahligen Werte ein. (Die aufgeführten Kommastellen sind gerundet.)
| Radius r | cm | dm | m | m |
| Durchmesser d | cm | dm | m | m |
| Volumen V | cm³ | dm³ | m³ | m³ |
| Oberfläche O | cm² | dm² | m² | m² |
richtig: 0falsch 0
Pyramiden- und Kegelstumpf
- Du kannst Oberfläche, Volumen, Seitenlängen und Höhe von Pyramiden- und Kegelstümpfen berechnen.
Aufgabe 21: Trage das Volumen des quadratischen Pyramidenstumpfes ein. Runde auf eine Nachkommastelle.
Der Pyramidenstumpf hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 22: Trage das Volumen des Kegelstumpfes ein. Runde auf eine Nachkommastelle.
Der Kegelstumpf hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 23: Trage die Höhe des quadratischen Pyramidenstumpfes ein. Runde auf ganze Zentimeter.
| a) | V = cm³; a1 = cm; a2 = cm h = cm |
| b) | V = cm³ a1 = cm; a2 = cm h = cm |
richtig: 0falsch: 0
Aufgabe 24: Trage die fehlenden Werte der Kegelstümpfe ein. Runde das Volumen (a) auf eine Nachkommastelle und die Höhe (b) auf ganze Zentimeter.
| a) | r1 = cm; r2 = cm; h = cm V = cm³ |
| b) | r1 = cm; r2 = cm; V = cm³ h = cm |
richtig: 0falsch: 0
Aufgabe 25: Der folgende Körper besteht aus einer quadratischen Pyramidenstumpf und einem Prisma. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 26: Der folgende Körper besteht aus einem Kegelstumpf und einem Zylinder. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Mehrstufige Zufallsversuche
- Du kannst die Wahrscheinlichkeit berechnen, mit der ein mehrstufiges Zufallsereignis eintrifft.
Aufgabe 27: | Aus dem unteren Sack werden 2 Kugeln nacheinander gezogen. Die zuerst gezogene Kugel wird nicht zurückgelegt. |
|||||
| a) | Wie groß ist die Wahrscheinlichkeit, dass zwei rote Kugeln gezogen werden? | |||||
| b) | Wie groß ist die Wahrscheinlichkeit, dass genau eine blaue Kugel gezogen wird? | |||||
|
Aufgabe von 15 |
||||||
| Antwort: | a) |
|
||||
| b) |
|
|||||
| Kürze die Ergebnisse soweit wie möglich! | ||||||
richtig: 0falsch: 0