Wurzel 
Das deutsche Wort Wurzel kommt vom lateinischen Wort radix. Der Kleinbuchstabe r wurde daher anfänglich auch als Wurzelzeichen verwendet. Später wurde das r über den ganzen Term verlängert und es entstand das heutige Wurzelzeichen √.
Anmerkung: Die Zahl 9 ist der Wert aus den Potenzen 32 sowie (-3)2. In der Mathematik ist der Wert einer Quadratwurzel (z.B. von 9) allerdings nur positiv: √9 = 3. Es geht nicht: √9 = -3.
Aufgabe 1: Trage die richtigen Begriffe ein.
- Das Wurzelziehen ist die Umkehrung zum (zotenPieren).
- Man fragt: "Welche Zahl, die mit sich selbst (plizultimiert) wird, ergibt den Wert unter dem Wurzelzeichen?"
- Der Wert unter dem Wurzelzeichen heißt (kadiRand).
- Quadratwurzeln haben (itposive) Ergebnisse.
- Quadratwurzeln können nicht aus negativen (kadiRanden) gebildet werden.
Versuche: 0
Aufgabe 2: Trage unten die richtige Wurzel ein.
| a) √ = | b) √ = | c) √ = |
richtig: 0falsch: 0
Aufgabe 3: Trage unten die richtigen Zahlen ein.
| Beispiel: 2² = 4, also ist √4 = 2 |
| a) ² = , also ist √ = |
| b) ² = , also ist √ = |
| c) ² = , also ist √ = |
richtig: 0falsch: 0
Aufgabe 4: Trage unten die richtigen Zahlen ein.
| Beispiel: √4 = 2; denn 2² = 4 |
| a) √ = ; denn ² = |
| b) √ = ; denn ² = |
| c) √ = ; denn ² = |
richtig: 0falsch: 0
Aufgabe 5: Trage unten die richtigen Zahlen ein.
| Beispiel: √4 = 2; denn 2² = 4 |
| a) √ = ; denn ² = |
| b) √ = ; denn ² = |
| c) √ = ; denn ² = |
richtig: 0falsch: 0
Aufgabe 6: Trage unten die Zahlen ein, die als Wurzel die Werte 1, 2, 3 ... haben.
| a | ||||||
| √a | 1 | 2 | 3 | 4 | 5 | 6 |
| a | ||||||
| √a | 7 | 8 | 9 | 10 | 11 | 12 |
Versuche: 0
Aufgabe 7: Ein Quadrat hat die Seitenlänge a und den Flächeninhalt a2. Trage die fehlenden Größen ein.
| a | m | m | m | m | |||
| a² | m² | m² | m² | m² |
richtig: 0falsch: 0
Aufgabe 8: Trage die Seitenlängen der Quadrate ein. Runde auf zwei Nachkommastellen.
| a) | b) | c) | ||
a) = m; b) = m; c) = m
richtig: 0falsch: 0
Aufgabe 9: Das kleine grüne Quadrat hat einen Flächeninhalt von 25 cm². Wie groß ist der Umfang des Rechtecks?
Das Rechteck hat einen Umfang von cm.
richtig: 0falsch: 0
Aufgabe 10: Die folgende Figur hat einen Flächeninhalt von . Trage unten den Umfang der Figur ein.
Die Figur hat einen Umfang von cm.
richtig: 0falsch: 0
Aufgabe 11: Trage den Radius des jeweiligen Kreises ein. Runde auf ganze Dezimeter.
| a) | b) | |
a) r = dm; b) r = dm
richtig: 0falsch: 0
Aufgabe 12: Bei den lila Flächen handelt es sich um Quadrate. Trage unten den Flächeninhalt von einem grünen Rechteck A1 ein.
| A1 | 16 cm2 |
| 81 cm2 | A1 |
A1 = cm2
Versuche: 0
Aufgabe 13: Trage den Flächeninhalt des roten (A) und des blauen (B) Quadrates ein.
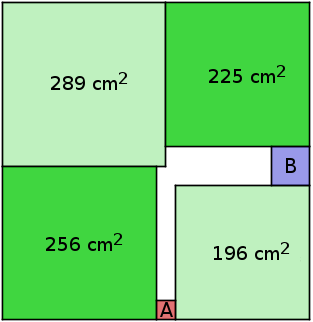
AA = cm2 | AB = cm2
richtig: 0falsch: 0
Aufgabe 14: Trage den Flächeninhalt von Quadrat A und B ein.
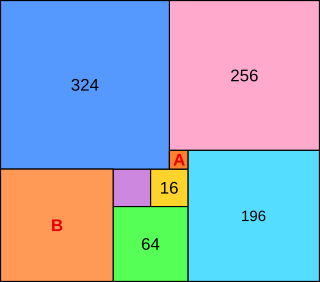
Maße in cm²
AA = cm2 | AB = cm2
Versuche: 0
Aufgabe 15: Die Oberfläche eines Spielwürfels beträgt 77,76 cm². Wie lang ist die Seite a des gekennzeichneten Spielsegmentes?
Das Segment ist cm lang.
Versuche: 0
Aufgabe 16: Das Prismennetz ist in gleich große Quadrate aufgeteilt. Die roten Bereiche bilden die Grund- und die Deckfläche. Der an den grauen Klebelaschen zusammengeklebte Körper hat ein Volumen von 14 739 cm3. Welche Mantelhöhe (a) hat das Prisma?
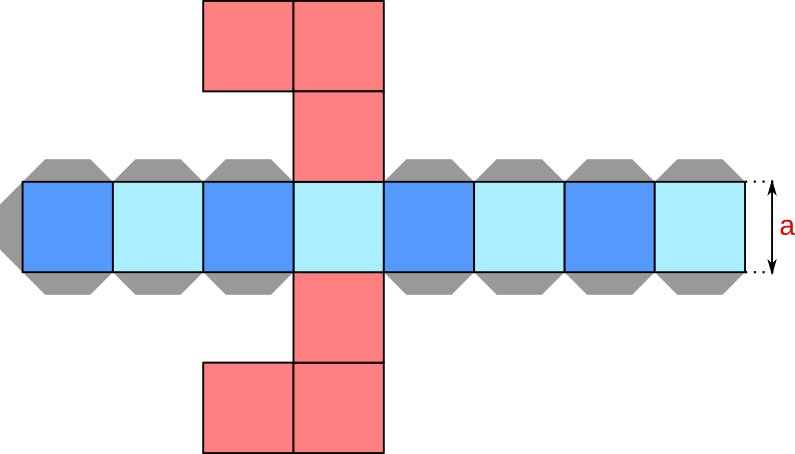
Der Mantel des Prismas (a) ist cm hoch.
Versuche: 0
Aufgabe 17: Die folgende Figur ist aus kleinen Würfeln zusammengesetzt und hat eine Oberfläche von .
| a) | Trage ein, aus wie vielen kleinen Quadraten die Oberfläche der Figur besteht. |
| b) | Gib die Kantenlänge eines kleinen Würfels an. |
| c) | Notiere das Volumen der gesamten Figur. |
| a) | Die Oberfläche besteht aus kleinen Quadraten. |
| b) | Ein kleiner Würfel hat eine Kantenläng von cm. |
| c) | Das Volumen der gesamten Figur beträgt cm3. |
richtig: 0falsch: 0
Aufgabe 18: Die untere Figur hat eine Oberfläche von . Wie groß ist ihr Volumen?
Die Figur hat ein Volumen von cm3.
richtig: 0falsch: 0
Aufgabe 19: Trage die fehlenden Ziffern ein.
a)  4 = 8 |
b) 14 = 12 |
| c) 11 = 11 |
d) 16 = 14 |
Versuche: 0
Aufgabe 20: Trage die fehlenden Ziffern ein. Die rötlich markierten Kästen haben die gleichen Ziffern.
| a) 19 = 13 |
b) 26 = 6 |
| c) 2 = 2 |
d) 59 = 2 |
Versuche: 0
Aufgabe 21: Berechne die Quadratwurzel. Runde auf ...
| a) zwei Stellen nach dem Komma. √ = |
b) drei Stellen nach dem Komma. √ = |
richtig: 0falsch: 0
Aufgabe 22: Klick auf den "Neu"-Button. Trage ein, zwischen welchen zwei natürlichen Zahlen die Quadratwurzel liegt.
| √ | ||||
| 9 | < | < | 16 | |
| 32 | < | < | 42 | |
| 3 | < | √ | < | 4 |
richtig: 0falsch: 0
Aufgabe 23: Trage als Lösung die richtigen Brüche ein.
| a) |
9 | = | b) |
25 | = | c) |
1 | = | |||
| 144 | 225 | 289 |
Versuche: 0
Aufgabe 24: Trage die Quadratwurzel ein.
|
= | ||
richtig: 0 | falsch: 0
Aufgabe 25: Trage die Lösung ein.
|
|
|
||||||||||||
|
|
|
||||||||||||
|
|
|
Versuche: 0
Aufgabe 26: Ein Rechteck ist 18 cm lang und 8 cm breit. Welche Seitenlänge hat ein Quadrat mit dem gleichen Flächeninhalt?
Das Quadrat hat eine Seitenlänge von cm.
Versuche: 0
Aufgabe 27: Ein Quadrat und ein Kreis haben den gleichen Flächeninhalt. Der Kreis hat einen Radius von 6,8 m. Wie groß ist die Seitenlänge des Quadrats? Rechne mit π = 3,14. Runde auf zwei Stellen nach dem Komma.
Das Quadrat hat eine Seitenlänge von m.
Versuche: 0
Aufgabe 28: Trage die Ergebnisse der Rechnungen ein.
| a) √9 + √25 = | b) √2,25 + 16 = |
| c) √¼ + 2,2 = | d) √16 + 3200 = |
Versuche: 0
Aufgabe 29: Trage die Ergebnisse ein. Rechne ohne Taschenrechner.
|
a) √9 + √16 + √4 = b) √49 + √36 + √81 = c) √400 - √121 - √25 = |
Versuche: 0
Aufgabe 30: Trage die Ergebnisse ein. Rechne ohne Taschenrechner.
|
a) √0,01 + √0,04 + √0,09 = b) √1,21 + √0,01 + √0,64 = c) |
Versuche: 0
Kubikwurzel
Es ist nicht nur möglich, eine Zahl aus der zweiten Potenz
herzuleiten - z.B die 9 aus 3 · 3 oder 32. Man
kann den Ursprung (die Wurzel) einer größeren Zahl auch aus der
dritten Potenz herleiten. Die 27 kann gesehen werden als
Ergebnis von 33 oder 3 · 3 · 3. Wird hier nach
dem Ursprung der größeren Zahl gefragt, dann spricht man von der
Kubikwurzel. Die Kubikwurzel von 27 ist 3. Mathematisch wird das
folgendermaßen geschrieben: 
27 = 3
Aufgabe 31: Fülle die Lücken mit den richtigen Werten.
|
|
||||||||
|
| ||||||||
|
|
Versuche: 0
Aufgabe 32: Ein Würfel hat das Volumen V = cm3. Wie lang ist die Würfelkante a?
a = cm
richtig: 0falsch: 0
Aufgabe 33: Berechne die Kantenlänge der Würfel mit folgendem Volumen.
| Volumen | Kantenlänge | |
| a) | cm³ | cm |
| b) | cm³ | cm |
| c) | cm³ | cm |
richtig: 0falsch: 0
Aufgabe 34: In einen Würfel passt genau 1 Liter hinein. Welche Kantenlänge hat er?
Der Würfel hat eine Kantenlänge von cm.
Versuche: 0
Aufgabe 35: Berechne den Oberflächeninhalt der Würfel mit folgendem Volumen.
| Volumen | Oberfläche | |
| a) | cm³ | cm² |
| b) | cm³ | cm² |
richtig: 0falsch: 0
Aufgabe 36: Die folgende Figur ist aus kleinen Würfeln zusammengesetzt. Der gesamte Körper hat ein Volumen von . Welche Kantenlänge hat der kleine grüne Würfel?
Der kleine grüne Würfel hat eine Kantenläng von cm.
richtig: 0falsch: 0
Aufgabe 37: Ein Quader ist 12 cm lang, 6 cm hoch und 3 cm breit. Welche Kantenlänge hat ein Würfel mit dem gleichen Volumen?
Der Würfel hat eine Kantenlänge von cm.
Versuche: 0
Aufgabe 38: Die untere Figur hat ein Volumen von . Trage unten ihre Oberfläche ein.
Die Figur hat eine Oberfläche von cm2.
richtig: 0falsch: 0
| Aufgabe 39: Bei mittlerem Sommerabfluss stürzen im Rheinfall etwa 700 Kubikmeter Wasser je Sekunde die Felsen hinunter. Welche Seitenlänge müsste ein würfelförmiges Aquarium haben, um die Wassermenge eines Tages aufnehmen zu können. Runde auf ganze Meter. Das würfelförmige Aquarium müsste mindestens eine Seitenlänge von m haben. Versuche: 0 |
|
n-te Wurzeln
|
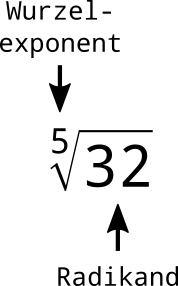
Bei Quadratwurzeln wird der Wurzelexponent nicht geschrieben. |
= 2
= 2
= 2
= 2Ergibt die n-te Potenz der Zahl a den Wert x, dann ergibt die n-te Wurzel des Wertes x die Zahl a.
Allgemein geschrieben: 
= a, denn an = x.
Aufgabe 40: Bestimme die Lösung ohne Taschenrechner.
a)  = |
b)  = |
c)  = |
d)  = |
e)  = |
f)  = |
g)  = |
h)  = |
i)  = |
Versuche: 0
Aufgabe 41: Rechne mit dem Taschenrechner. Runde die Lösung auf zwei Nachkommastellen.
|
|
|
richtig: 0falsch: 0
Aufgabe 42: Trage die fehlenden Werte in die Tabelle ein. Runde auf zwei Stellen nach dem Komma.
| a) | b) | c) | d) | e) | |
| x | 81 | 625 | |||
 |
36 | ||||
 |
16 | ||||
 |
4 |
Versuche: 0
Aufgabe 43: Trage die richtigen Werte ein.
|
|
|
||||||||||||||||||||||||||||||||||||
richtig: 0falsch: 0
Aufgabe 44: Trage die richtigen Werte ein.
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
richtig: 0falsch: 0
Aufgabe 45: Trage die richtigen Wurzelexponenten(n) und Radikanden(x) ein.
| n = |
| n = | ||||||||||||
| x = | x = | ||||||||||||||
| n = |
| n = | ||||||||||||
| x = | x = | ||||||||||||||
| n = |
| n = | ||||||||||||
| x = | x = | ||||||||||||||
Versuche: 0
Aufgabe 46: Ordne die Terme mit demselben Wert einander zu.
Aufgabe 47: Ordne die Terme mit demselben Wert einander zu.