Quadratische Gleichung
- In quadratischen Gleichungen taucht die gesuchte Variable in quadrierter Form (x²) auf.
Rein quadratische Gleichung
- In rein quadratischen Gleichungen kommt die Variable nur in quadrierter Form (x²
x) vor.
Aufgabe 1: Trage den positiven Wert von x1 ein. Der entsprechende negative Wert x2 wird automatisch angezeigt.
| a) x² = ; x1 = ; x2 = - | b) x² = ; x1 = ; x2 = - | ||||||||||||||||||||||
|
|
||||||||||||||||||||||
|
f) -x² = - ; x1 = ; x2 = - |
richtig 0falsch 0
Aufgabe 2: Trage den positiven Wert von x1 ein. Der entsprechende negative Wert x2 wird automatisch angezeigt.
| a) x² = ; x1 = ; x2 = - | |||||||||
| b) x² = ; x1 = ; x2 = - | |||||||||
|
|||||||||
|
|||||||||
| f) -x² = ; x1 = ; x2 = - |
richtig 0falsch 0
Aufgabe 3: Trage jeweils den Betrag (ohne Vorzeichen) für x ein.
|
a) (x + 3) · (x - 3) = 0; x1 = ; x2 = - b) (x - 5) · (x + 5) = 0; x1 = ; x2 = - c) (x + 2)² = 4x + 40; x1 = ; x2 = - |
Versuche: 0
Aufgabe 4: Trage die beiden Lösungen der jeweiligen Gleichung so ein, dass der x1-Wert größer ist als der x2-Wert.
| x1 > x2 | |
| a) | x1 = ; x2 = |
| b) | x1 = ; x2 = |
| c) | x1 = ; x2 = |
richtig: 0falsch: 0
Aufgabe 5: Stelle die Reglern der Grafik so ein, dass die in der Tabelle aufgeführten Gleichungen in der Grafik links unten erscheinen. Übertrage die x-Werte in die entsprechenden Textfelder.
Info: Die Nullstellen einer Funktionsgleichung können als Lösung einer quadratische Gleichung ausgelegt werden. Wie quadratische Funktionen eine, zwei oder keine Nullstelle aufweisen, können quadratische Gleichungen eine, zwei oder keine Lösung haben.
| a) x² - 4 = 0; x1 = ; x2 = | b) 4x² - 4 = 0; x1 = ; x2 = |
| c) -x² + 4 = 0; x1 = ; x2 = | d) -4x² + 4 = 0; x1 = ; x2 = |
| e) 0,5x² - 2 = 0; x1 = ; x2 = | f) 2x² - 2 = 0; x1 = ; x2 = |
| g) -0,5x² + 2 = 0; x1 = ; x2 = | h) -2x² + 2 = 0; x1 = ; x2 = |
| i) x² = 0; x = | j) 2x² = 0; x = |
| k) -x² = 0; x = | l) -2x² = 0; x = |
| m) x² + 4 = 0 | n) 4x² + 4 = 0 |
| o) -0,5x² -2 = 0 | p) -2x² -2 = 0 |
Versuche: 0
Aufgabe 6: Klick an, ob die Gleichung keine, eine oder zwei Lösungen hat. Fünfzehn Gleichungen sind zuzuordnen.
| Lösungen: | ||
x² < 0 |
x² = 0 |
x² > 0 |
richtig: 0 | falsch: 0
Gemischt quadratische Gleichung
- Gleichungen, die sowohl die Variable x als auch ihr Quadrat x² aufweisen, nennt man gemischt quadratische Gleichung.
- Die Normalform einer gemischt quadratischen Gleichung ist x² + px + q = 0.
- Die p,q-Formel
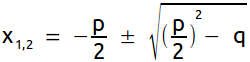 dient zur Lösung der Gleichung.
dient zur Lösung der Gleichung. 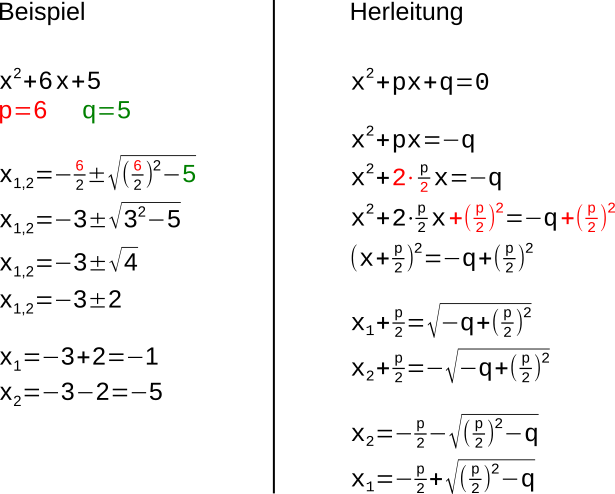
Aufgabe 7: Trage die Werte der Koeffizienten p und q jeweils ein.
| a) | p = | q = | b) | p = | q = |
| c) | p = | q = | d) | p = | q = |
| |||
Aufgabe 8: Löse die Gleichung mithilfe der p,q-Formel. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
| a) | x1 = | x2 = | b) | x1 = | x2 = |
| c) | x1 = | x2 = | d) | x1 = | x2 = |
| |||
Aufgabe 9: Bringe zuerst die Gleichungen auf die Normalform. Berechne dann die Variablen. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
| a) | x1 = | x2 = | b) | x1 = | x2 = |
| c) | x1 = | x2 = | d) | x1 = | x2 = |
| |||
Aufgabe 10: Forme die Gleichung zuerst um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
| a) | x1 = | x2 = | b) | x1 = | x2 = |
| c) | x1 = | x2 = | d) | x1 = | x2 = |
| |||
Aufgabe 11: Forme die Gleichung zuerst um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
| a) | x1 = | x2 = | b) | x1 = | x2 = |
| c) | x1 = | x2 = | d) | x1 = | x2 = |
| |||
Aufgabe 12: Löse die Klammer auf und trage die entsprechenden Beträge in die Textfelder unterhalb der Gleichung ein. Stelle die Gleichung anschließend in die Normalform um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
richtig: 0falsch: 0
Aufgabe 13: Löse alle Klammern auf und trage die entsprechenden Beträge in die Textfelder unterhalb der Gleichung ein. Stelle die Gleichung anschließend in die Normalform um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
richtig: 0falsch: 0
Aufgabe 14: Löse alle Klammern auf und trage die entsprechenden Beträge in die Textfelder unterhalb der Gleichung ein. Stelle die Gleichung anschließend in die Normalform um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
richtig: 0falsch: 0
Aufgabe 15: Stelle die Gleichung in die Normalform um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
-14 + (x + 1)² - x² + 2x - 1 = x · (2 - x) + 49
x1 = ; x2 =
Versuche: 0
Aufgabe 16: Stelle die Gleichung in die Normalform um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
(x + 3) · (x + 4) - 5 = -6 · (x - 9) + 1 3 (36x - 15)
x1 = ; x2 =
Versuche: 0
Aufgabe 17: Stelle die Gleichung in die Normalform um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
(x + 3) · (x - 3) = -3 · (x + 9) + (2x + 6)²
x1 = ; x2 =
Versuche: 0
Aufgabe 18: Stelle die Gleichung in die Normalform um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
x 2 · (4x + 8) + 2 = -3x · (2x - 7)
x1 = ; x2 =
Versuche: 0
Aufgabe 19: Stelle die Gleichung in die Normalform um. Trage als x1 das Ergebnis ein, das durch das Addieren der Wurzel entsteht und als x2 den Wert, der durch das Subtrahieren der Wurzel zustandekommt.
(4x - 3)² - 2 · (x - 1)² - 7x · (2x + 1)= -x² - 3x · (x - 1) + 67 - 38x
x1 = ; x2 =
Versuche: 0
Info: Die Anzahl der Lösungen einer quadratischen Gleichung lässt sich durch den Term unterhalb der Wurzel bestimmen. Dieser Term heißt Diskriminante (D).
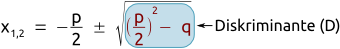
- D > 0 (positiv): Die Gleichung hat zwei Lösungen.
- D = 0: Die Gleichung hat eine Lösung.
- D < 0 (negativ): Die Gleichung hat keine Lösung.
Aufgabe 20: Klick an, ob die Gleichung keine, eine oder zwei Lösungen hat. Zwölf Gleichungen sind zuzuordnen.
| Lösungen: | ||
D < 0 |
D = 0 |
D > 0 |
richtig: 0 | falsch: 0
Aufgabe 21: Die Zahl x wird mit der Zahl (x + 1) multipliziert. Das Ergebnis ist .
x1 = ; x2 =
richtig: 0 | falsch: 0
Aufgabe 22: Zwei Zahlen unterscheiden sich um . Ihr Produkt ergibt . Die kleinere der beiden Zahlen ist x.
x1 = ; x2 =
richtig: 0 | falsch: 0
Aufgabe 23: Multipliziert man das Dreifache einer Zahl mit der um verkleinerten Zahl, so erhält man .
x1 = ; x2 =
richtig: 0 | falsch: 0
Aufgabe 24: Das Produkt aus einem Viertel einer Zahl und dem um vergrößerten Doppelten der Zahl ist .
x1 = ; x2 =
richtig: 0 | falsch: 0
Aufgabe 25: Ein rechteckiges Grundstück hat eine Fläche von m² und ist von einem langen Zaun umgeben. Wie lang und wie breit ist das Grundstück?
Antwort: Das Grundstück hat eine Länge von Metern und eine Breite von Metern.
richtig: 0falsch: 0
Aufgabe 26: Ein rechteckiges x m² großes Baugrundstück wird durch einen Zaun gesichert. Eine Seite ist x m länger als die andere. Wie viel Meter Zaun werden benötigt?
Hinweis: Die Länge eines Grundstücks kann nicht negativ sein.
Antwort: Der Zaun ist Metern lang.
richtig: 0falsch: 0
Aufgabe 27: Verkürzt man bei einem Quadrat zwei parallele Seiten um und verlängert die anderen beiden um , so entsteht ein Rechteck mit einem Flächeninhalt von . Welchen Flächeninhalt hat das anfängliche Quadrat?
Hinweis: Die Länge eines Quadrates kann nicht negativ sein.
Antwort: Das Quadrat hat einen Flächeninhalt von m².
richtig: 0falsch: 0
Aufgabe 28: Die Schüler einer Klasse erhalten den Auftrag ein Din A4 Blatt (210 mm x 297 mm) so zu einer Schale zu falten, dass die Grundfläche der Schale zwei Drittel des ursprünglichen Din A4 Blattes beträgt. Wie hoch ist der Rand der Schale (x)?
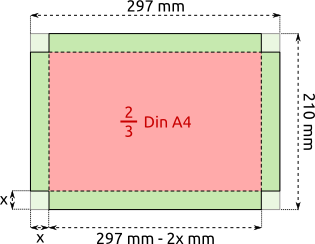
Antwort: Bei ganz genauem Falten wäre der Rand der Schale mm hoch.
Versuche: 0
Aufgabe 29: Die Grundseite c eines rechtwinkligen Dreiecks ist x cm länger als die zugehörige Höhe hc. Der Flächeninhalt des Dreiecks beträgt x cm². Wie lang ist die Seite c?
Antwort: Die Seite c ist cm lang.
richtig: 0falsch: 0
Aufgabe 30: Quadrat A und Quadrat B haben zusammen einen Flächeninhalt von und x + y = . Welche Flächeninhalte haben die zwei Quadrate?
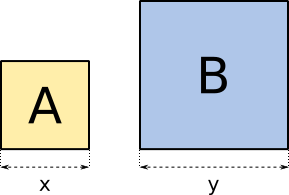
Das kleine Quadrat A hat einen Flächeninhalt von cm2 und das große Quadrat B einen von cm2.
richtig: 0falsch: 0
Aufgabe 31: Auf einem Platz mit einer Länge von 50 Metern und einer Breite von 20 Metern soll eine Gärtnerei vier Blumenbeete anlegen. 90 % der Platzfläche stehen für die Beete zur Verfügung, 10 % teilen sich zwei mittig verlaufende, gleich breite Wege. Wie groß ist die Breite x der Wege? Runde auf Zentimeter.
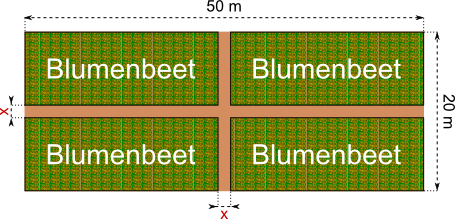
Antwort: Die Wege sind m breit.
Versuche: 0
Aufgabe 32: Der Oberflächeninhalt eines langen Prismas (b) beträgt . Die Grundfläche des Prismas ist eine Raute mit einem 150° Winkel. Wie lang ist eine Seite (a) der Grundflächenraute?
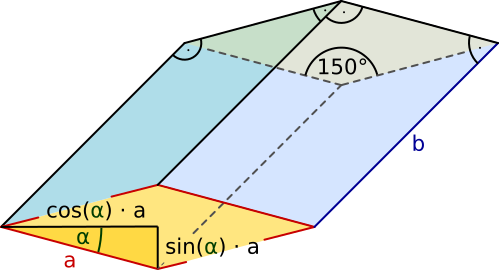
Die Raute hat eine Seitenlänge (a) von cm.
richtig: 0falsch: 0
Aufgabe 33: Ein Kegel hat eine Oberfläche (O = πr² + πrs) von 14π cm². Die Seitenlänge des Kegelmantels beträgt s = 5 cm. Wie groß ist der Radius r der Grundfläche?
Der Radius r beträgt cm.
Versuche: 0
Aufgabe 34: Die Zahl wird so in zwei Summanden zerlegt, dass deren Produkt beträgt. Trage die Ergebnisse so ein, dass x1 größer als x2 ist.
x1 = | x2 =
Eintrag: x1 > x2
richtig: 0falsch: 0
Aufgabe 35: Trage die fehlenden Werte der Funktionsgleichungen ein, mit denen die Parabeln der Springseile beschrieben werden.
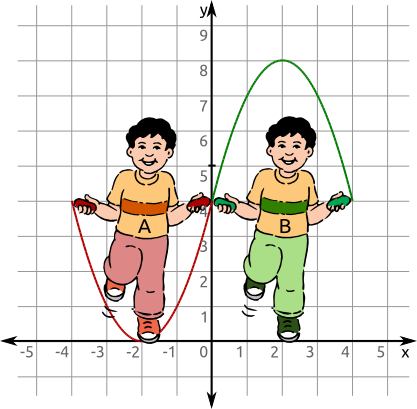
A: y = ()² B: y = -()²
Versuche: 0
Aufgabe 36: Ergänze die Funktionsgleichungen so, dass sie zu den Graphen passen.
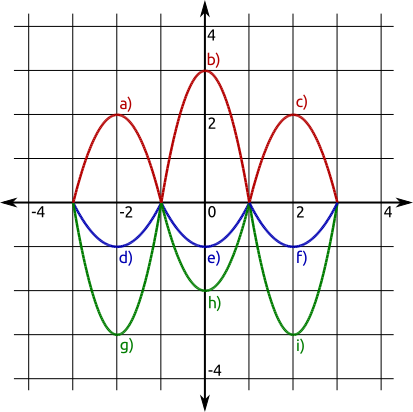
|
a) y = b) y = c) y = |
d) y = e) y = f) y = |
g) y = h) y = i) y = |
Versuche: 0
Besondere Punkte in Funktionen ermitteln
Um die folgenden Aufgaben lösen zu können, müssen besondere Punkte einer Funktion ermittelt werden. Da eine Funktion aus mehreren Unbekannten besteht, kann sie für diese Punkte nur gelöst werden, wenn ihre Variablen mit Zahlen gefüllt werden. Für die unten angegebenen Bereiche lassen sich Zahlen bestimmen:
|
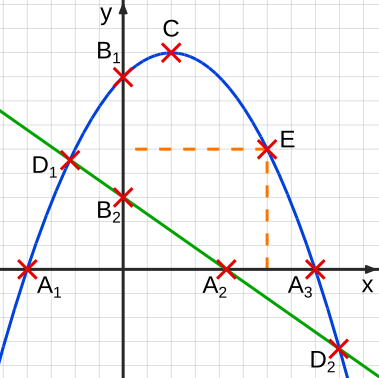 |
Aufgabe 37: Bestimme die beiden Nullstellen und den Schnitt mit der y-Achse der folgenden Funktionen. Trage bei den Nullstellen den größeren Wert bei x1 ein.
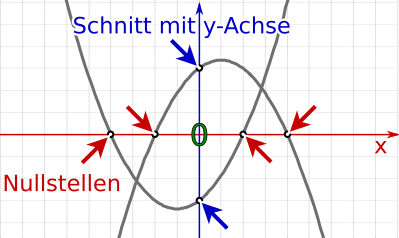
| a) |
Nullstellen: x1 = | x2 = Schnitt mit y-Achse: y = |
||
| b) |
Nullstellen: x1 = | x2 = Schnitt mit y-Achse: y = |
||
| c) |
Nullstellen: x1 = | x2 = Schnitt mit y-Achse: y = |
||
| d) |
Nullstellen: x1 = | x2 = Schnitt mit y-Achse: y = |
||
Eintrag: x1 > x2
richtig 0falsch 0
Aufgabe 38: Die Parabel der Funktion y = ax2 + c schneidet die y-Achse bei und geht durch den Punkt P(). Bestimme den Streckfaktor a.
a =
richtig: 0falsch: 0
Aufgabe 39: Von der Parabel y = ax2 + c sind der Scheitelpunkt S(0|) und der Punkt P() bekannt. Trage unten die fehlende Koordinate des Punktes Q ein, der ebenfalls auf der Parabel liegt.
Q( | )
richtig: 0falsch: 0
Aufgabe 40: Gib die Koordinaten für den Scheitelpunkt an. Bestimme die beiden Nullstellen der folgenden Funktion. Die Stellen, an denen der Graph die x-Achse berührt. Trage den größeren Wert bei x1 ein.
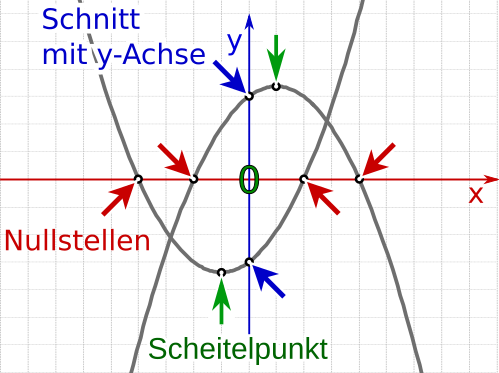
Eintrag: x1 > x2
richtig: 0falsch: 0
Aufgabe 41: Bestimme die beiden Nullstellen der folgenden Funktion. Die Stellen, an denen der Graph die x-Achse berührt. Trage den größeren Wert bei x1 ein.
Eintrag: x1 > x2
richtig: 0falsch: 0
Aufgabe 42: Die Parabel der Funktion y = a(x + b)2 + c mit dem Scheitel S() geht durch den Punkt P(). Bestimme den Streckfaktor a.
a =
richtig: 0falsch: 0
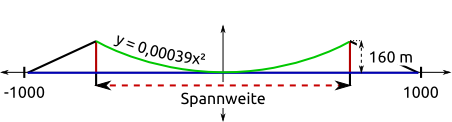
Aufgabe 43: Die Stützpfeiler der Golden Gate Bridge ragen ca 160 Meter über die Fahrbahn hinaus. Das Tragseil dazwischen wird annähernd durch die Funktion y = 0,00039x² beschrieben. Wie groß ist die Spannweite zwischen den Pfeilern? Runde auf 10 Meter.
Antwort: Die Spannweite beträgt 0 m.
Versuche: 0
Aufgabe 44: Das Tragseil der folgenden Brücke wird durch die Funktion y = a · x2 beschrieben. Die vertikalen Seile sind in gleichmäßigem Abstand angeordnet. Wie groß ist die Variable a der Funktion und wie lang sind die vertikalen Seile s1 und s2?
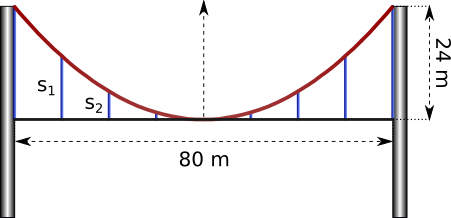
a = s1 = m s2 = m
Versuche: 0
Aufgabe 45: Die Flugbahn eines Fußballs nach einem Schuss lässt sich beschreiben mit der Gleichung: y = - 1 28 x2 + 7. Wie hoch ist der Ball, wenn er horizontal - vom Abschuss bis zum ersten Aufprall - ¼ seiner Strecke geflogen ist?
Der Ball befindet sich in einer Höhe von m.
Versuche: 0
Aufgabe 46: Unten siehst du die Flugbahnen unterschiedlich hart geschlagener Golfbälle. Trage die entsprechende Flugweite ein.
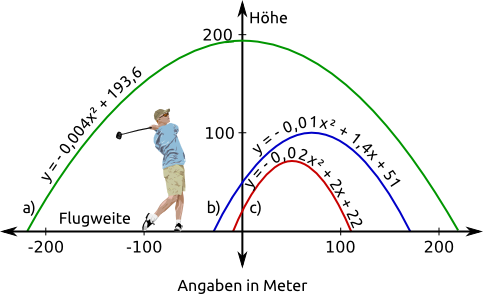
Antwort: a) m; b) m; c) m
Versuche: 0
Aufgabe 47: |
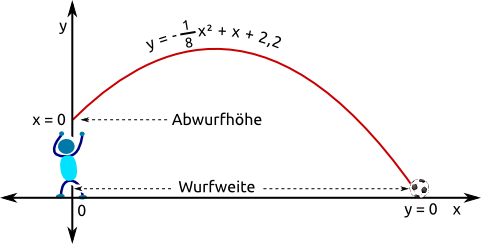
Marko macht beim Fußball einen Einwurf. Die Flugbahn wird annähernd mit folgender Funktion beschrieben: y = -0,125x² + x + 2,2. |
| Antwort: | a) Der Ball fliegt m weit. (Runde auf cm) b) Der Ball verlässt in einer Höhe von m Markos Hände. |
Versuche: 0
Aufgabe 48: |
Jens spritzt mit seiner Wasserpistole aus 1,40 m Höhe in verschiedenen Winkeln und in unterschiedlich starker Intensität. Der jeweilige Wasserstrahl hat die Form folgender Parabel: A: y = -0,5x² + 0,5x + 1,4
B: y = -0,25x² + 0,8x + 1,4 C: y = -0,2x² + 1,1x + 1,4 Trage auf den Zentimeter genau ein, in welcher Entfernung der jeweilige Strahl auf dem Boden auftrifft (2 Nachkommastellen). |
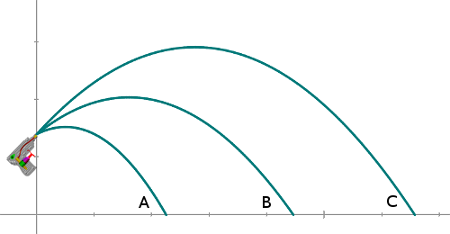
Antwort: Strahl A spritzt m, Strahl B m und Strahl C m weit.
Versuche: 0
Aufgabe 49: Eine Brücke wird durch einen parabelförmigen Bogen gestützt. Er hat eine Spannweite von und ragt in die Höhe. Trage den richtigen Streckfaktor in die Funktionsgleichung des Bogens ein.
y = x2
richtig: 0falsch: 0
Schnittpunkte zweier Funktionen bestimmen
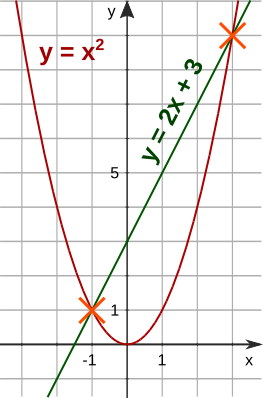
An ihren Schnittpunkten haben zwei Funktionen den gleichen x-Wert und den gleichen y-Wert. Um den Schnittpunkt zu bestimmen, können die beiden Funktionen wie ein lineares Gleichungssystem aufgefasst werden. Beispiel: Die Funktionen y = x2 und y = 2x + 3 haben an ihren Schnittpunkten den gleichen y-Wert.
 |
|
Die Schnittpunkte liegen bei S1(-1|1) und bei S2(3|9).
Aufgabe 50: Berechne jeweils den Schnittpunkt der beiden Funktionen.
|
a) y = x² y = 0,5x + 3 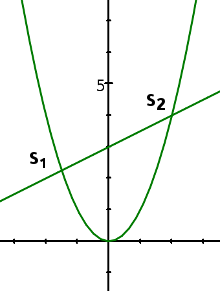
S1(|)
S2(|) Versuche: 0 |
b) y = x² - 4 y = x + 2 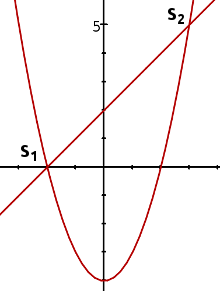
S1(|)
S2(|) Versuche: 0 |
c) y = -2x² - 3x + 2 y = -2x - 1 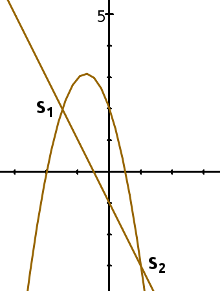
S1(|)
S2(|) Versuche: 0 |
Aufgabe 51: Trage unten die Schnittpunkte der beiden Funktionen ein. Trage den Schnittpunkt mit dem kleineren x-Wert bei S1 ein.
S1(|) S2(|)
richtig: 0falsch: 0
Aufgabe 52: Trage unten die Schnittpunkte der beiden Funktionen ein. Rechne immer mit allen Nachkommastellen. Runde erst zum Schluss auf eine Nachkommastelle.
S1(|) S2(|)
Runde auf Zehntel
richtig: 0falsch: 0
Aufgabe 53: Der Bogen der abgebildeten Brücke kann durch die Funktionsgleichung y = -0,05 · (x - 10)2 + 20 beschrieben werden. |
|
| a) | Wie lang ist der Abstand zwischen Punkt A und Punkt B. |
| b) | Wie lang ist die Strecke a? |
Eine Längeneinheit entspricht 1 m.
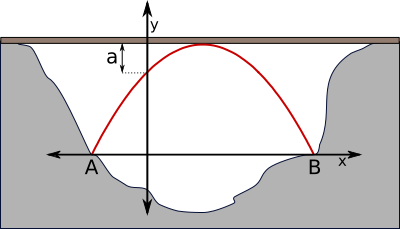
| a) | Der Abstand zwischen Punkt A und Punkt B beträgt Meter. |
| b) | Die Strecke a ist Meter lang. |
Versuche: 0
Aufgabe 54: In der unteren Graphik wird angezeigt, wie aus einem 32 cm langen Blech ein Kanal zu biegen ist, der einen größtmöglichen, rechtwinkligen Querschnitt (gelb) aufweisen soll.
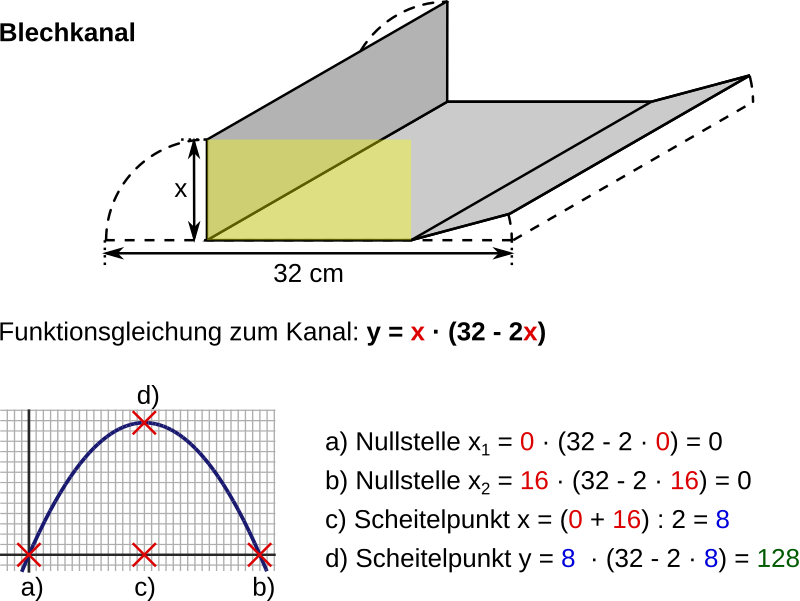
Berechne die Seitenhöhe (x) und den größtmöglichen, rechtwinkligen Querschnitt für einen Kanal, der aus einem Blech von Länge erstellt werden würde.
Ein solcher Kanal wäre cm hoch. Er hätte einen Querschnitt von cm2.
richtig: 0falsch: 0