Pyramide 
Eine Pyramide ist ein Körper, der aus einem Vieleck (Drei-, Vier-, Fünfeck ...) und mehreren Dreiecken besteht. Das Vieleck bildet die Grundfläche und die Dreiecke die Mantelfläche der Pyramide.
Ein Klick auf das Thema führt dich zu den Aufgaben.
- Grundkenntnisse (A 1 - A 5)
- Berechnungsgrundlagen (A 6)
- Volumen (A 7 - A 14)
- Oberfläche (A 15 - A 20)
- Gemischte Größen (A 21 - A 24)
- Satz des Pythagoras (A 25 - A 37)
- Sachaufgaben (A 38 - A 43)
- Pyramidengrundfläche ist kein Viereck (A 44 - A 46)
- Trigonometrie (A 47 - A 51)
Grundkenntnisse
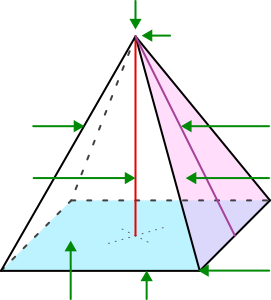
Aufgabe 1: Klicke die richtigen Begriffe an.
|
Höhe der
auch Ecke
Ecke
|
Versuche: 0
Aufgabe 2: Wie viele Eckpunkte, Kanten und Flächen hat eine Pyramide über folgenden Grundflächen?
| a) | b) | c) | d) |
| Grundfläche | Ecken | Kanten | Flächen |
| a) Dreieck | |||
| b) Viereck | |||
| c) Fünfeck | |||
| d) Sechseck | |||
| Erkennst du eine Regel? | |||
| e) Siebeneck | |||
| f) Achteck | |||
| g) Neuneck | |||
Versuche: 0
Aufgabe 3: Markiere alle Netze, aus denen man Pyramiden falten kann, mit einem Klick.
Versuche: 0
Aufgabe 4: Verschiebe die orangen Gleiter so, dass das Netz einer quadratischen Pyramide entsteht.
richtig: 0 | falsch: 0
Aufgabe 5: Welche Eckpunkte des Netzes treffen sich, wenn man es zu einer Pyramide faltet?
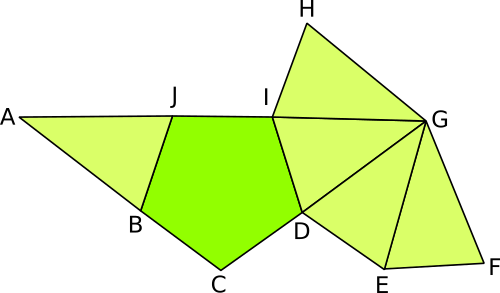
Es treffen sich: A und , B und , C und , H und .
Versuche: 0
Berechnungsgrundlagen
Berechnung des Volumens (V)
Das Pyramidenvolumen hat 3-mal Platz im Volumen eines Quaders mit gleicher Grundfläche und gleicher Höhe. Um das Pyramidenvolumen (V) zu berechnen, wird die Volumenformel des Quaders "Grundfläche (G) · Höhe (h)" durch drei geteilt.
| V = | G · h |
| 3 |
Berechnung der Oberfläche (O)
Die Oberfläche einer Pyramiden besteht aus den Dreiecken der Mantelfläche und der Grundfläche. Die Grundfläche besteht aus einem Vieleck. Für die Berechnung des Oberflächeninhaltes einer Pyramide mit quadratischer Grundfläche gilt folgende Formel:
O = a² + 4 · a · ha 2 oder O = a² + 2a · ha
Achtung! Die Höhe der Manteldreiecke unterscheidet sich von der Pyramidenhöhe.
Aufgabe 6: Ziehe an den orangen Gleitern der Grafik und beobachte, wie sich die Pyramide und das Pyramidenetz verändern.
Formeln
Die untere Tabelle gibt an, wie Oberfläche und Volumen der Pyramide berechnet werden. Grundsätzlich gilt:
- Oberfläche = Grundfläche + Mantelfläche
- Volumen = Grundfläche · Pyramidenhöhe : 3
Generell ist darauf zu achten, dass mit unterschiedlichen Höhenangaben gerechnet wird. Für die Berechnung der Oberfläche wird die Höhe der schrägliegenden Seitendreiecke benötigt (Grafik unten: ha; hb). Für die Berechnung des Volumens wird die Höhe der Pyramide benutzt (Grafik unten: h).
| rechteckige Grundfläche | quadratische Grundfläche |
|
Oberfläche
= Grundfläche
+ Mantelfläche OP = AG + AM |
|
| OP = a · b + a · ha + b · hb | OP = a² + a · ha · 2 |
|
Volumen
= Grundfläche
· h : 3 VP = AG · h : 3 |
|
| VP = a · b · h : 3 | VP = a² · h : 3 |
Volumen
Aufgabe 7: Trage das Volumen der Pyramide unten ein.
Maße in cm
V = cm³
richtig: 0falsch: 0
Aufgabe 8: Trage das Volumen der Pyramide mit der dargestellten Grundfläche und einer Körperhöhe von 6,9 cm ein.
Angaben in cm
Va = cm³; Vb = cm³; Vc = cm³;
richtig: 0falsch: 0
Aufgabe 9: Trage das Volumen der Doppelpyramide ein.
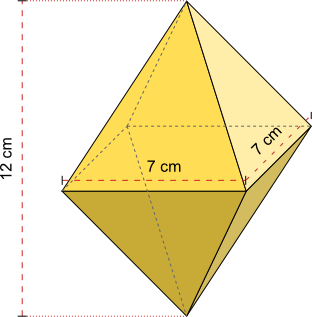
Die Doppelpyramide hat ein Volumen von cm³.
Versuche: 0
Aufgabe 10: Der folgende Körper besteht aus zwei quadratischen Pyramiden. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 11: Der folgende Körper besteht aus einer quadratischen Pyramide und einem Quader. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 12: Aus einem Quader mit einer quadratischen Grundfläche wurde eine Pyramide ausgehöhlt. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 13: Trage das Volumen des folgenden Werkstücks (Würfel mit pyramidenförmiger Aushöhlung) ein. (Die gerundeten Nachkommastellen sind vorgegeben!)
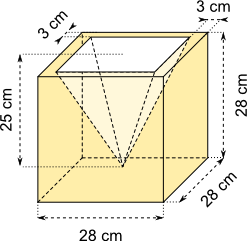
Der ausgehöhlte Würfel hat ein Volumen von ,92 dm³
Versuche: 0
Aufgabe 14: Gestalte mit Hilfe der orangen Gleiter eine quadratische Pyramide mit einem Volumen von cm³. Die roten Linien markieren Höhe und Breite. Sinnvoll einstellbar sind als Breite 4, 8, 12 und 16 cm. Als Höhe sind 3 bis 15 cm möglich.
Keine Kavaliersperspektive
Kästchenlänge: 1 cm
richtig: 0 | falsch: 0
Oberfläche
Aufgabe 15: Trage die Grund-, die Mantel- und die Oberfläche der quadratischen Pyramide ein.
| Grundfläche: | cm2 |
| Mantelfläche: | cm2 |
| Oberfläche: | cm2 |
richtig: 0falsch: 0
Aufgabe 16: Trage Grundfläche, Mantelfläche und Oberfläche der Pyramiden ein.
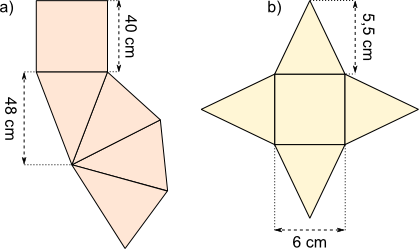
| a) | b) | |
| Grundfläche | cm² | cm² |
| Mantelfläche | cm² | cm² |
| Oberfläche | cm² | cm² |
Versuche: 0
Aufgabe 17: Trage die Oberfläche der quadratischen Pyramide unten ein.
Maße in cm
O = cm²
richtig: 0falsch: 0
Aufgabe 18: Trage die Oberfläche der folgenden Pyramide unten ein.
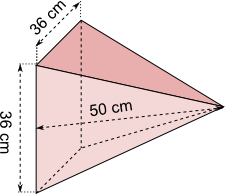
Die Pyramide hat eine Oberfläche von cm².
Versuche: 0
Aufgabe 19: Berechne die fehlenden Werte der quadratischen Pyramiden.
| a) AG = cm² | AM = cm² | O = cm² |
| b) AG = cm² | AM = cm² | O = cm² |
| c) a = cm | hDreieck = cm | O = cm² |
| d) a = cm | hDreieck = cm | O = cm² |
AG: Grundfläche; AM: Mantelfläche; O: Oberfläche
richtig: 0falsch: 0
Aufgabe 20: Gestalte mit Hilfe der orangen Gleiter ein Pyramidennetz mit einer Oberfläche von cm².
Kästchenlänge: 1 cm
richtig: 0 | falsch: 0
Gemischte Größen
Aufgabe 21: Trage die fehlenden Größen der quadratischen Pyramiden mit allen Nachkommastellen ein.
| a | h | AG | V | |
| a) | a0 | h0 | cm | cm3 |
| b) | a1 | h1 | m | m3 |
| c) | a2 | m | m | V2 |
AG: Grundfläche; V: Volumen
richtig: 0falsch 0
Aufgabe 22: Trage Volumen und Oberfläche der quadratischen Pyramiden ein. Runde auf 2 Stellen nach dem Komma.
| Grundkante a | cm | dm | m |
| Dreieckshöhe ha | cm | dm | m |
| Pyramidenhöhe hP | cm | dm | m |
| Volumen V | cm³ | dm³ | m³ |
| Oberfläche O | cm² | dm² | m² |
richtig: 0falsch 0
Aufgabe 23: Trage die fehlenden Größen der Pyramiden ein.
| Grundkante a | cm | dm | m | m |
| Grundkante b | cm | dm | m | m |
| Pyramidenhöhe h | cm | dm | m | m |
| Volumen V | cm³ | dm³ | m³ | m³ |
richtig: 0falsch 0
Aufgabe 24: Das Volumen einer quadratischen Pyramide beträgt . Eine Seite der Grundfläche ist lang. Welche Höhe hat die Pyramide?
Die Pyramide hat eine Höhe von cm.
richtig: 0falsch: 0
Satz des Pythagoras
Aufgabe 25: Klick unten auf "Auto" und du kannst erkennen, wo in einer Pyramide u.a. rechtwinklige Dreiecke vorhanden sind, deren Seiten durch den Satz des Pythagoras zu ermitteln sind. Mit den Pfeil-Buttons kannst du von Bild zu Bild navigieren.
© 2000 - http://geonext.de
 |
|||||
|
Aufgabe 26: Betrachte die beiden Grafiken und finde heraus, welche Größe unten gesucht wird. Trage sie ein.
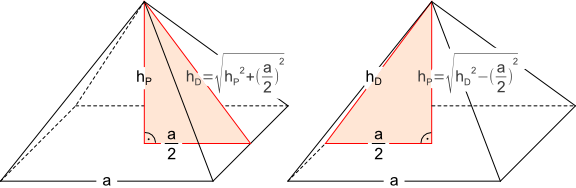
a = Seitenlänge; hP = Pyramidenhöhe; hD = Höhe des Manteldreiecks
| Antwort: | = |
|
Versuche: 0
Aufgabe 27: Berechne die Oberfläche der folgenden Pyramide. Beachte die Größenangaben. Runde auf ganze dm².
Maße in cm
O = dm²
richtig: 0falsch: 0
Aufgabe 28: |
a) Ermittle die Höhe des Seitendreiecks mithilfe des Satzes von Pythagoras. b) Berechne die Oberfläche der Pyramide. c) Rechne die Höhe der Pyramide aus. (Die gerundeten Nachkommastellen sind vorgegeben!) d) Berechne das Volumen der Pyramide. (Die gerundeten Nachkommastellen sind vorgegeben!) |
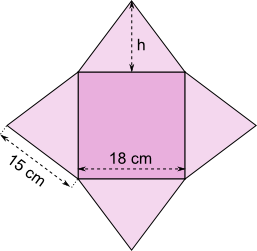 |
|
Antwort: |
a) Die Höhe des Seitendreiecks beträgt cm. b) Die Pyramide hat eine Oberfläche von cm². c) Die Höhe der Pyramide ist ,94 cm. d) Die Pyramide hat ein Volumen von ,22 cm³. |
Versuche: 0
Aufgabe 29: Berechne das Volumen der folgenden Pyramide. Beachte die Größenangaben. Runde auf ganze dm³.
Maße in cm
V = dm³
richtig: 0falsch: 0
Aufgabe 30: Berechne mit den vorhandenen Angaben verschiedener quadratischer Pyramiden die folgenden Größen.
| a | hP | hs | AG | AM | O | V |
| cm | cm | cm | 576 cm² | 1776 cm² | cm² | cm³ |
| cm | cm | cm | 1024 cm² | cm² | 3200 cm² | cm³ |
| cm | cm | cm | 12544 cm² | cm² | cm² | 376320 cm³ |
Versuche: 0
Aufgabe 31: Eine quadratische Pyramide hat eine Mantelfläche von . Die Länge der Grundseite beträgt . Wie groß ist das Volumen der Pyramide?
Das Volumen beträgt cm³.
richtig: 0falsch: 0
Aufgabe 32: Aus einem 20 cm breiten Würfel wird mit 2 cm Kantenabstand auf jeder Seite die Form einer 8 cm tiefen Pyramide ausgehöhlt. Welche Oberfläche hat der so entstandene Körper? Runde das Ergebnis auf ganze Quadratzentimeter.
Der Körper hat eine Oberfläche von cm².
Versuche: 0
Aufgabe 33: Trage die Länge der Diagonale (d) und die Pyramidenhöhe (h) ein.
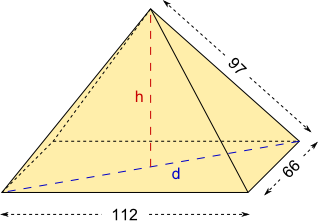
Angaben in cm
Antwort: |
a) Die Länge der Diagonale beträgt cm. b) Die Pyramide hat eine Höhe von cm. |
Versuche: 0
Aufgabe 34: Berechne das Volumen der quadratischen Pyramide (inkl. Quader) und des halb so hohen Quaders.
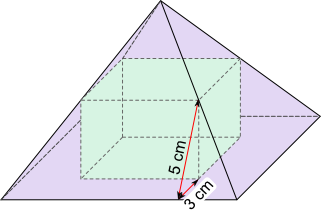
VPyramide = cm³; VQuader = cm³
Versuche: 0
Aufgabe 35: Trage die fehlenden ganzzahligen Werte für die gesuchten Strecken einer quadratischen Pyramide ein. Hier muss der Satz des Pythagoras einige Male angewendet werden.
Bastelvorlage eines Pyramidenschnitts herunterladen
Hinweis: ![]()
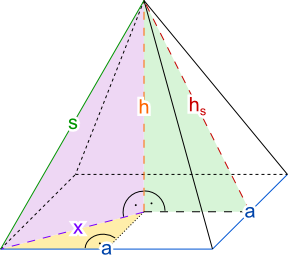 |
 |
| a | s | h | hs | |
| a) | 16 cm | cm | ,7 cm | 15 cm |
| b) | 48 dm | 74 dm | ,8 dm | dm |
| c) | mm | 65 mm | ,2 mm | 56 mm |
| d) | ,6 cm | 53 cm | 45 cm | ,2 cm |
Versuche: 0
Aufgabe 36: Im roten Würfel befindet sich ein gelbes Oktaeder (Achtflächler), dessen Oberfläche aus gleichseitigen Dreiecken besteht. Die Spitzen des Oktaeders treffen genau die Mitte der Würfelflächen. Der Würfel hat eine Kantenlänge von . Wie groß ist das Volumen und die Oberfläche des gelben Oktaeders? Trage die fehlenden Werte ein.
VOktaeder = cm³ | OOktaeder = , cm²
richtig: 0falsch: 0
Aufgabe 37: Eine quadratische Pyramide hat die Grundkante (a) 10 cm und die Höhe (h) 12 cm. In diese Pyramide ist ein Dreieck schräg eingelagert.
- Dreieckspunkt A berührt die untere, linke Spitze.
- Dreieckspunkt B berührt die Mitte der rechten Grundkante.
- Dreieckspunkt C berührt die Mitte der vorderen, rechten Seitenkante.
Trage den Umfang des Dreiecks ein. Runde auf ganze Zentimeter.
Das Dreieck hat einen Umfang von cm.
Versuche: 0
Sachaufgaben
Aufgabe 38: |
Ein pyramidenartiges Zelt mit rechteckiger Grundfläche ist 2,60 m lang, 2,00 m breit und 3 m hoch. a) Gib das Volumen des Zeltes an. b) Aus wie viel m² Zeltplane (ohne Boden) besteht das Zelt? (Die gerundeten Nachkommastellen sind vorgegeben!) |
||||
|
Versuche: 0

Die Pyramide hatte ein Volumen von ,33 Königsellen³.
Versuche: 0
Aufgabe 40: Moderne Lang-Lkw (Gigaliner) können bis zu 25,25 m lang sein und weisen ein Ladevolumen von 157 m³ auf. Die "Königselle" ist in Aufgabe 33 mit 52,3 cm angegeben. Wie viele Gigaliner wären nötig, um bei diesem Umrechnungswert das Volumen der ursprünglichen Pyramide aus Aufgabe 26 abzutransportieren? Runde auf Hunderter.

Um das Volumen der ursprünglichen Pyramide abzutransportieren, wären Gigaliner notwendig.
Versuche: 0
Aufgabe 41: Ein Kirchturmdach hat die Form einer quadratischen Pyramide. Die Seiten der Grundfläche haben eine Länge von . Die Pyramidenspitze befindet sich über der Grundfläche. Berechne die Dachfläche des Kirchturms und trage den ganzzahligen Wert deines Ergebnisses ein.
Der Kirchturm hat eine Dachfläche von m²
richtig: 0falsch: 0
Aufgabe 42: Eine quadratische Pyramide aus Aluminium (Dichte = 2,7 g/cm³) hat eine Grundseite von und wiegt . Wie hoch ist die Pyramide?
Die Pyramide hat eine Höhe von cm.
richtig: 0falsch: 0
Aufgabe 43: Ein Werkstück aus Messing (Dichte = 8,5 g/cm³) besteht aus einer quadratischen Pyramide mit einer zylinderförmigen Vertiefung. Berechne Oberfläche, Volumen und Gewicht. Trage den ganzzahligen Wert des gerundeten Ergebnisses ein.
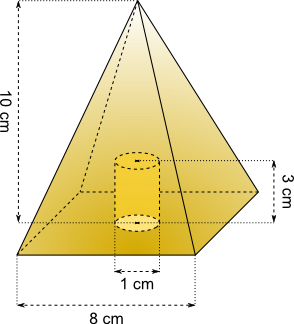
Oberfläche = ,8 cm²; Volumen = ,0 cm³; Gewicht = ,3 g
Versuche: 0
Pyramidengrundfläche ist kein Viereck
Aufgabe 44: Bei einem regelmäßigen Tetraeder (Körper aus vier gleichseitigen Dreiecken) ist die Seitenkante (s) lang. Trage unten den ganzzahligen Wert des Oberflächeninhalts ein. Berechne zuerst die Höhe der Dreiecksseite (hs).
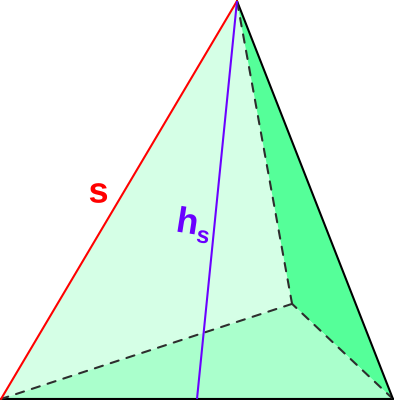 |
O = , cm²
richtig: 0falsch: 0
Aufgabe 45: Eine Pyramide hat als Grundfläche ein regelmäßiges Sechseck mit einer Seitenlänge (a) von 6 cm. Die Höhe eines Seitendreiecks (hs) beträgt hs. Wie groß ist die Oberfläche dieser Pyramide? Trage den fehlenden ganzzahligen Wert unten ein.
Die Oberfläche beträgt , cm²
richtig: 0falsch: 0
Aufgabe 46: Eine Pyramide besteht aus 4 gleichseitigen Dreiecken (gelb). An jede ihrer Seiten wird passend eine genauso große Pyramide geklebt (rot, grün, pink, blau). Welches Volumen und welchen Oberflächeninhalt hat der so aus 5 Pyramiden neu entstandene, zusammengesetzte Körper, wenn die Seitenkante (s) einer Pyramide 40 cm lang ist? Trage den ganzzahligen Wert ein.
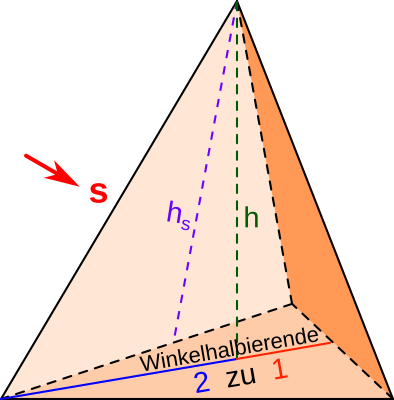 |
Hilfe: Die Pyramidenhöhe (h) schneidet die Winkelhalbierende der Grundfläche in einem Verhältnis von 2:1 (siehe Grafik).
O = , cm² | V = , cm³
richtig: 0falsch: 0
Trigonometrie
Aufgabe 47: Eine quadratische Pyramide ist 220 m lang. Ihre Spitze wird 161 m von der Bodenkante entfernt in einem Winkel von 22° angepeilt. Wie hoch ist die Pyramide? Runde auf eine Nachkommastelle.
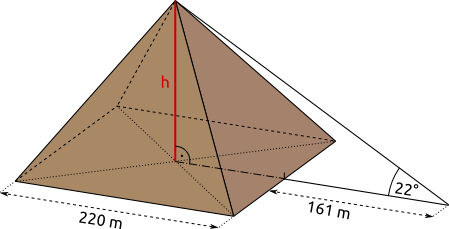
Die Pyramide hat eine Höhe von m.
Versuche: 0
Aufgabe 48: Berechne a) das Volumen und b) den Oberflächeninhalt einer quadratischen Pyramide mit einer Parallelschnittfläche, die folgende Größen aufweist: und . Runde das Ergebnis auf ganze Kubik- und Quadratzentimeter.
| a) V = cm³ | b) O = cm² | |
|
|
Aufgabe 49: Berechne a) das Volumen und b) den Oberflächeninhalt einer quadratischen Pyramide mit einer Diagonalschnittfläche, die folgende Größen aufweist: und . Runde das Ergebnis auf ganze Kubik- und Quadratzentimeter.
| a) V = cm³ | b) O = cm² | |
|
|
Aufgabe 50: Unten siehst du eine regelmäßige sechsseitige Pyramide. Trage die Größe des markierten Winkel α ein. Runde auf eine Nachkommastelle.
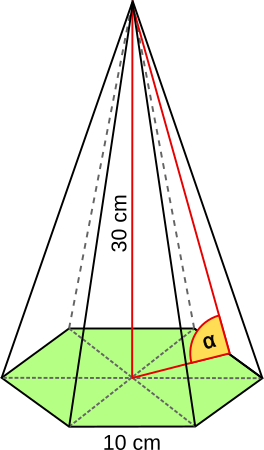
α = °
Versuche: 0
Aufgabe 51: Aus einer quadratischen Pappe mit der Seitenlänge wird der Mantel einer quadratischen Pyramide ausgeschnitten. Welches Volumen hat die Pyramide? Runde auf ganze Kubikzentimeter.
Die Pyramide hat ein Volumen von cm³.
richtig: 0falsch: 0

