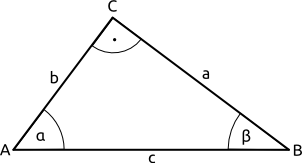
Trigonometrie 
Ein Klick auf das Thema führt dich zu den Aufgaben.
- Ankathete, Gegenkathete, Hypotenuse (A 1 - A 7)
- Sinusaufgaben (A 8 - A 17)
- Kosinusaufgaben (A 18 - A 25)
- Tangensaufgaben (A 26 - A 33)
- Leicht erkennbare rechtwinklige Dreiecke (A 34 - A 46)
- Allgemeine Dreiecke (A 47 - A 60)
- Flächenformel im allgemeinen Dreieck (A 61 - A 62)
- Rechtwinklige Dreiecke in Vielecken (A 63 - A 74)
- Rechtwinklige Dreiecke in Körpern (A 75 - A 84)
Ankathete, Gegenkathete, Hypotenuse
Aufgabe 1: Trage unten die richtigen Begriffe ein.
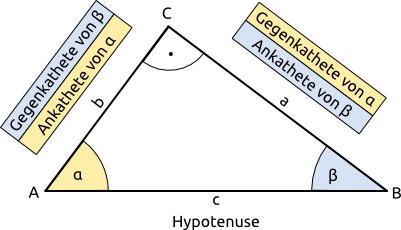
- In der Trigonometrie geht es um Seitenverhältnisse in (reinchtwilkeng) Dreiecken.
- Die längste Seite, (geberügen) dem rechten Winkel, nennt man (potenHyseu).
- Die beiden kurzen Seiten heißen (atKethen).
- Die (kAntheate) liegt an einem Winkel an.
- Die (genkatheGete) liegt einem Winkel gegenüber.
- Folgende Seitenverhältnisse werden unterschieden:
| (nusSi) = | Gegenkathete | (Konussi) = | Ankathete | (Tensang) = | Gegenkathete |
| Hypotenuse | Hypotenuse | Ankathete |
Versuche: 0
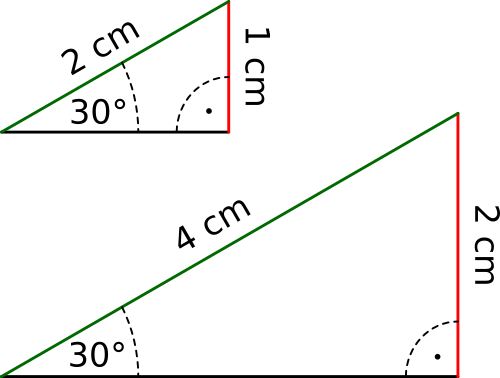
Die Trigonometrie macht sich die Ähnlichkeit von Dreiecken zunutze. Hat ein rechtwinkliges Dreieck wie im rechten Beispiel einen Winkel von 30°, dann liegt das Längenverhältnis zwischen der roten und der grünen Linie bei 1 zu 2 (½). Ist also die rote Strecke 1 cm lang, dann ist die grüne Strecke 2 cm lang. Misst die rote Strecke 2 cm, dann misst die grüne Strecke 4 cm usw. Bei rechtwinkligen Dreiecken sind für jeden beliebigen Winkel mittels Taschenrechner die jeweilige Seitenverhältnisse abrufbar. Das ermöglicht es entweder, mit einem Winkel und einer Seitenlänge die zweite Seitenlänge zu bestimmen oder mit zwei Seitenlängen den dazugehörigen Winkel zu bestimmen.
| Beispiel: | |
| Winkel | → 30° |
| Seitenverhältnis (rot/grün) | → ½ |
| gegebene grüne Strecke | → 6 cm |
| gesuchte rote Strecke | → 6 cm · ½ = ? cm |
Aufgabe 2: Ordne die Farbwörter des Klappmenüs den richtigen Farben der Dreiecksseiten zu.
Aufgabe 3: Trage die fehlenden Begriffe ein.
- Achte vor deinen Berechnungen auf den (erchten) Winkel des zugrunde liegenden Dreiecks.
- Finde die (merFol), in der (ziwe) von drei Größen gegeben sind.
- Löse nach der (bekUntannen) hin auf und berechne den gesuchten Wert.
Versuche: 0
Info: Das Längenverhältnis der Seiten bei einem entsprechenden Winkel wird folgendermaßen bezeichnet:
- Der Sinus (kurz: sin) eines Winkels ist das Längenverhältnis aus der Gegenkathete dieses Winkels und der Hypotenuse.
sin φ = Gegenkathete sin α = a ; sin β = b Hypotenuse c c
- Der Kosinus (kurz: cos) eines Winkels ist das Längenverhältnis aus der Ankathete dieses Winkels und der Hypotenuse.
cos φ = Ankathete cos α = b ; cos β = a Hypotenuse c c
- Der Tangens (kurz: tan) eines Winkels ist das Längenverhältnis aus der Gegenkathete dieses Winkels und der Ankathete.
tan φ = Gegenkathete tan α = a ; tan β = b Ankathete b a
Aufgabe 4: Trage die Buchstaben der Seiten so ein, dass die Sinus-, die Kosinus- und die Tangensangaben richtig sind.
| Sinus | Kosinus | Tangens | ||||||||||||||||||||
|
a1)
|
b1)
|
c1)
|
||||||||||||||||||||
|
a2)
|
b2)
|
c2)
|
Versuche: 0
Aufgabe 5: Klick an, um welchen Wert es sich handelt. Wenn zwei Werte richtig sind, klick beide an.
| a | = |
| c |
richtig: 0falsch: 0
Aufgabe 6: Bewege den orangen Eckpunkt des Dreiecks und beobachte, wie sich seine x- und y-Werte verändern, wenn die Hypotenuse des Dreiecke die Länge 1 hat. Kontrolliere die Werte, indem du mit dem Taschenrechner den jeweiligen Sinus- und Kosinuswert des aufgeführten Winkels ermittelst. (Die hier ausgegebenen Werte sind gerundet.)
Aufgabe 7: Trage jeweils die fehlenden Seitenbezeichnungen ein.

| sin α = | = | = | cos α = | = | = | tan α = | = | = | |||||||||
| b | c | a | b | c | a | c | n | h | |||||||||
| sin β = | c | = | h | = | n | cos β = | a | = | m | = | h | tan β = | c | = | h | = | n |
Versuche: 0
Aufgabe 8: Stelle den Winkel α des Dreiecks mit Hilfe des weißen Gleiters auf die jeweilige Gradzahl der Tabelle ein. Übertrage dann die gesuchten Werte.
|
||||||||||||||||||||||
| Dreieck | α | a1 | c1 |
|
||||
| a) | 10° | 1,74 cm | 10 cm | 0,174 | ||||
| b) | 20° | cm | 10 cm | |||||
| c) | 30° | cm | 10 cm | |||||
| d) | 40° | cm | 10 cm | |||||
| e) | 50° | cm | 10 cm | |||||
| f) | 60° | cm | 10 cm | |||||
| g) | 70° | cm | 10 cm | |||||
| h) | 80° | cm | 10 cm |
Versuche: 0
Aufgabe 9: Trage die Buchstaben der Seiten so ein, dass die Sinusangaben richtig sind.
| a) | b) | ||||||||||||
 |
 |
||||||||||||
|
|
Versuche: 0
Aufgabe 10: Trage die Sinuswerte der angezeigten Winkel in die Textfelder ein. Runde auf die vierte Nachkommastelle.
| a) | sin ° = | b) | sin ° = |
| c) | sin ° = | d) | sin ° = |
richtig: 0falsch: 0
Info: Seitenlängen mit dem Sinus berechnen
Der Sinus eines Winkels ermöglicht es beim rechtwinkligen Dreieck, die Länge seiner Gegenkathete oder der Hypotenuse zu berechnen.
a = sin α · c
|
b = sin β · c
|
Aufgabe 11: Berechne die Länge der roten Seiten und trage sie in das zugehörige Textfeld ein. Runde auf eine Nachkommastelle.
| a) | b) | |
 |
 |
|
| a = cm | b = cm | |
| c) | d) | |
 |
 |
|
| c = cm | c = cm |
Versuche: 0
Aufgabe 12: Ein Dreieck hat die Winkel
Antwort: Die Seite ist cm lang. Runde auf eine Stelle nach dem Komma.
richtig: 0falsch: 0
Info: Einen Winkel im rechtwinkligen Dreieck mit Hilfe des Seitenverhältnisses von Gegenkathete zu Hypotenuse (Sinus) berechnen.
Teilt man die Gegenkathete eines Winkels durch die Hypotenuse , so erhält man seinen Sinuswert. Wird dieser Wert in die Umkehrfunktion des Sinus (Arkussinus) eingegeben, so erhält man die Größe des Winkel.
Beispiel:
- a = 3 cm; c = 6 cm; γ = 90°
3 = sin α = 0,5 6 - α = 30° (Arkussinus von 0,5)
Aufgabe 13: Trage die Winkel zu den angegebenen Sinuswerten ein. Runde auf ganze Gradangaben.
| a) | sin α = | b) | sin α = |
| α = ° | α = ° | ||
| c) | sin β = | d) | sin β = |
| β = ° | β = ° | ||
richtig: 0falsch: 0
Aufgabe 14: In einem Dreieck ist der Winkel γ rechtwinklig (90°). Runde auf ganze Gradangaben.
| a) | Wie groß ist der Winkel α, wenn sin β = ? |
| b) | Wie groß ist der Winkel β, wenn sin α = ? |
Antwort: α = °; β = °
richtig: 0falsch: 0
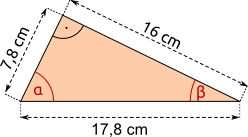
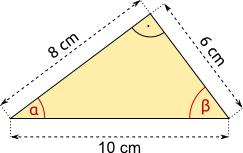
Aufgabe 15: Bestimme die Winkel α und β. Runde auf eine Nachkommastelle.
| a) | b) | |
 |
 |
|
| α = ° β = ° | α = ° β = ° |
Versuche: 0
Aufgabe 16: Trage den gesuchten Winkel (α oder β) des rechtwinkligen Dreiecks mit γ = 90° ein. Runde auf ganze Gradangaben.
α = °
richtig: 0falsch: 0
Aufgabe 17: Wie groß ist bei folgender Skaterrampe der Steigungswinkel α? Runde auf eine Nachkommastelle.
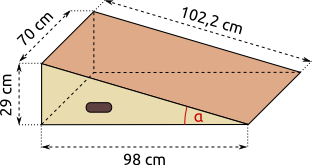
Antwort: Der Steigungswinkel α beträgt °
Versuche: 0
Aufgabe 18: Trage die Buchstaben der Seiten so ein, dass die Kosinusangaben richtig sind.
| a) | b) | ||||||||||||
 |
 |
||||||||||||
|
|
Versuche: 0
Aufgabe 19: Trage die Kosinuswerte der angezeigten Winkel in die Textfelder ein. Runde auf die vierte Nachkommastelle.
| a) | cos ° = | b) | cos ° = |
| c) | cos ° = | d) | cos ° = |
richtig: 0falsch: 0
Info: Seitenlängen mit dem Kosinus berechnen
Der Kosinus eines Winkels ermöglicht es beim rechtwinkligen Dreieck, die Länge seiner Ankathete oder der Hypotenuse zu berechnen.

b = cos α · c
|
a = cos β · c
|
Aufgabe 20: Berechne die Länge der roten Seiten und trage sie in das zugehörige Textfeld ein. Runde auf eine Nachkommastelle.
| a) | b) | |
 |
 |
|
| a = cm | b = cm | |
| c) | d) | |
 |
 |
|
| c = cm | c = cm |
Versuche: 0
Aufgabe 21: Ein Dreieck hat die Winkel
Antwort: Die Seite ist cm lang. Runde auf eine Stelle nach dem Komma.
richtig: 0falsch: 0
Info: Einen Winkel im rechtwinkligen Dreieck mit Hilfe des Seitenverhältnisses von Ankathete zu Hypotenuse (Kosinus) berechnen.
Teilt man die Ankathete eines Winkels durch die Hypotenuse, so erhält man seinen Cosinuswert. Wird dieser Wert in die Umkehrfunktion des Kosinus (Arkuskosinus) eingegeben, so erhält man die Größe des Winkel.
Beispiel:
- b = 3 cm; c = 6 cm; γ = 90°
3 = cos α = 0,5 6 - α = 60° (Arkuskosinus von 0,5)
Aufgabe 22: Trage die Winkel zu den angegebenen Kosinuswerten ein. Runde auf ganze Gradangaben.
| a) | cos α = | b) | cos α = |
| α = ° | α = ° | ||
| c) | cos β = | d) | cos β = |
| β = ° | β = ° | ||
richtig: 0falsch: 0
Aufgabe 23: In einem Dreieck ist der Winkel γ rechtwinklig (90°). Runde auf ganze Gradangaben.
| a) | Wie groß ist der Winkel α, wenn cos β = ? |
| b) | Wie groß ist der Winkel β, wenn cos α = ? |
Antwort: α = °; β = °
richtig: 0falsch: 0
Aufgabe 24: Bestimme die Winkel α und β. Runde auf ganze Gradangaben.
| a) | b) | |
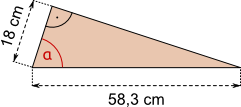 |
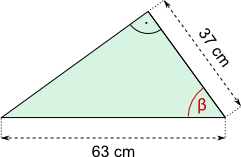 |
|
| α = ° | β = ° |
Versuche: 0
Aufgabe 25: Trage den gesuchten Winkel (α oder β) des rechtwinkligen Dreiecks mit γ = 90° ein. Runde auf ganze Gradangaben.
α = °
richtig: 0falsch: 0
Aufgabe 26: Trage die Buchstaben der Seiten so ein, dass die Tangensangaben richtig sind.
| a) | b) | ||||||||||||
 |
 |
||||||||||||
|
|
Versuche: 0
Aufgabe 27: Trage die Tangenswerte der angezeigten Winkel in die Textfelder ein. Runde auf die vierte Nachkommastelle.
| a) | tan ° = | b) | tan ° = |
| c) | tan ° = | d) | tan ° = |
richtig: 0falsch: 0
Info: Seitenlängen mit dem Tangens berechnen
Der Tangens eines Winkels ermöglicht es beim rechtwinkligen Dreieck, die Länge seiner Gegenkathete oder seiner Ankathete zu berechnen.

a = tan α · b
|
b = tan β · a |
Aufgabe 28: Berechne die Länge der roten Seiten und trage sie in das zugehörige Textfeld ein. Runde auf eine Nachkommastelle.
| a) | b) | |
 |
 |
|
| a = cm | b = cm | |
| c) | d) | |
 |
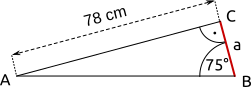 |
|
| b = cm | a = cm |
Versuche: 0
Aufgabe 29: Ein Dreieck hat die Winkel
Antwort: Die Seite ist cm lang. Runde auf eine Stelle nach dem Komma.
richtig: 0falsch: 0
Info: Einen Winkel im rechtwinkligen Dreieck mit Hilfe des Seitenverhältnisses von Gegenkathete zu Ankathete (Tangens) berechnen.
Teilt man die Gegenkathete eines Winkels durch seine Ankathete, so erhält man seinen Tangenswert. Wird dieser Wert in die Umkehrfunktion des Tangens (Arkustangens) eingegeben, so erhält man die Größe des Winkel.
Beispiel:
- a = 5 cm; b = 5 cm; γ = 90°
5 = tan α = 1 5 - α = 45° (Arkustangens von 1)
Aufgabe 30: Trage die Winkel zu den angegebenen Tangenswerten ein. Runde auf ganze Gradangaben.
| a) | tan α = | b) | tan α = |
| α = ° | α = ° | ||
| c) | tan β = | d) | tan β = |
| β = ° | β = ° | ||
richtig: 0falsch: 0
Aufgabe 31: In einem Dreieck ist der Winkel γ rechtwinklig (90°). Runde auf ganze Gradangaben.
| a) | Wie groß ist der Winkel α, wenn tan β = ? |
| b) | Wie groß ist der Winkel β, wenn tan α = ? |
Antwort: α = °; β = °
richtig: 0falsch: 0
Aufgabe 32: Bestimme die Winkel α und β. Runde auf ganze Gradangaben.
| a) | b) | |
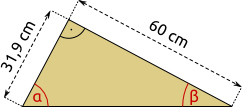 |
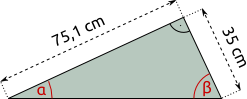 |
|
| α = ° β = ° | α = ° β = ° |
Versuche: 0
Aufgabe 33: Trage den gesuchten Winkel (α oder β) des rechtwinkligen Dreiecks mit γ = 90° ein. Runde auf ganze Gradangaben.
α = °
richtig: 0falsch: 0
Aufgabe 34: Ein Dreieck hat die Winkel
Antwort: Die Seite ist cm lang. Runde auf eine Stelle nach dem Komma.
richtig: 0falsch: 0
Aufgabe 35: Trage den gesuchten Winkel (α oder β) des rechtwinkligen Dreiecks mit γ = 90° ein. Runde auf ganze Gradangaben.
α = °
richtig: 0falsch: 0
Aufgabe 36: Trage den Flächeninhalt des Dreiecks ein. Runde das Ergebnis auf eine Nachkommastelle.
A = cm²
richtig: 0falsch: 0
Aufgabe 37: Trage den Flächeninhalt des Dreiecks ein. Runde das Ergebnis auf eine Nachkommastelle.
A = cm²
richtig: 0falsch: 0
Aufgabe 38: Klick in den Winkelfunktionen die zum Dreieck passenden Werte an.
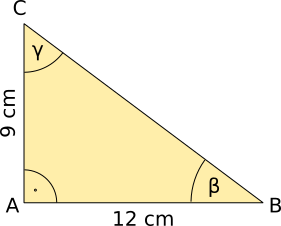
| cos β = | cos γ = | ||
Versuche: 0
Aufgabe 39: Die Strecke eines Seifenkistenrennens weist auf den ersten 40 Metern ein Gefälle von 18° auf. Die folgenden 116 Meter bis zum Ziel haben ein Gefälle von 8°. Welcher Höhenunterschied besteht zwischen Start und Ziel? Runde auf eine Nachkommastelle.
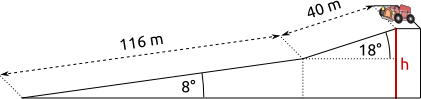
Der Start der Rennstrecke liegt m über dem Ziel.
Versuche: 0
Aufgabe 40: |
Zwei ein Meter breite Mauern stehen parallel im Abstand von 6,50 m zueinander. Die eine ist 7,00 m die andere 4,08 m hoch. Der Zimmermann soll beide Mauern mit einem Schrägdach verbinden. |
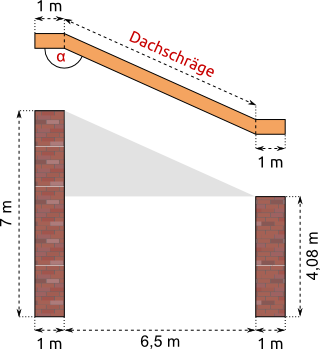
a) Der Winkel α beträgt °. (Runde auf eine Nachkommastelle.) |
Versuche: 0
Aufgabe 41: Die Talstation einer Seilbahn befindet sich in einer Höhe von 1 258 m. Der durchschnittliche Steigungswinkel beträgt α = 15°. Das Stahlseil hat eine Länge von 2,5 km. Trage die Höhe der Bergstation ein. Runde auf ganze Meter.
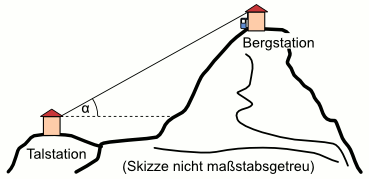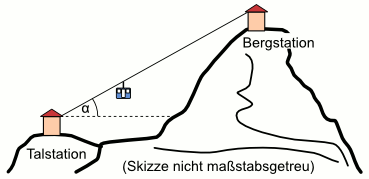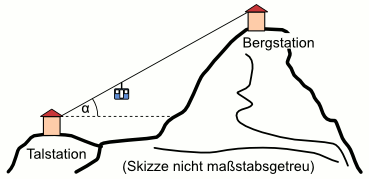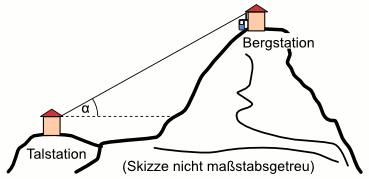
Die Bergstation befindet sich in einer Höhe von m.
Versuche: 0
Aufgabe 42: Trage die Länge der Strecke CD ein. Runde auf eine Nachkommastelle.
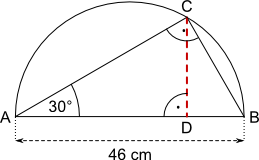
Die Strecke CD ist cm lang.
Versuche: 0
Aufgabe 43: |
a) Trage die Länge der Strecke CD ein. Runde auf zwei Nachkommastellen. |
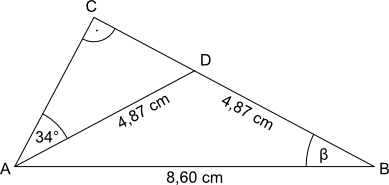
| a) Die Strecke CD ist cm lang. b) Der Winkel β beträgt °. |
Versuche: 0
Aufgabe 44: Die Seiten einer Stehleiter haben eine Länge von 3 Metern. Der Öffnungswinkel beträgt 42°. Welche Höhe hat die Leiter? Runde auf cm.
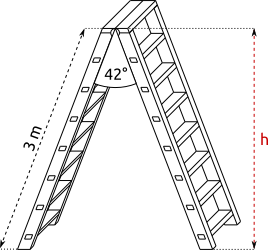
Die Leiter hat eine Höhe von m.
Versuche: 0
Aufgabe 45: Trage die Länge der Sehne s ein. Runde auf eine Nachkommastelle.
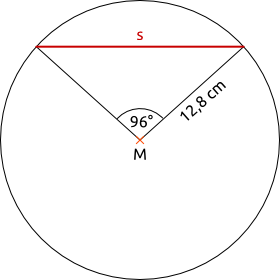
Die Sehne ist cm lang.
Versuche: 0
Aufgabe 46: Trage die Länge der roten Seite x unten ein.

x = cm
Versuche: 0
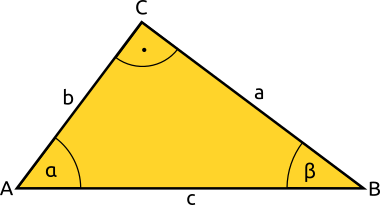
Allgemeine Dreiecke
Zerlegst du allgemeine Dreiecke über ihre Höhe in rechtwinklige Dreiecke, dann kannst du mithilfe von Sinus, Kosinus und Tangens fehlende Seiten und Winkel berechnen.
Aufgabe 47: Klick auf den unteren "weiter"-Button und sieh dir an, wie die fehlenden Größen eines allgemeinen Dreiecks berechnet werden können.
Beispiel:
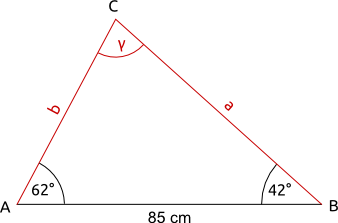
Ein allgemeines Dreieck hat die Winkel α 62° und β 42°. Die Seite c ist 85 cm lang.
Aufgabe 48: Berechne den Winkel γ sowie die Seiten a und b. Trage die ganzzahligen Ergebnisse unten ein.
γ = °; a = , cm; b = , cm
richtig: 0falsch: 0
Aufgabe 49: Die Entfernung zwischen zwei Leuchttürmen beträgt . Von Leuchtturm A ist das Schiff in einem Winkel von zu sehen. An Leuchtturm B beträgt der Winkel . Wie weit ist das Schiff von beiden Leuchttürmen entfernt? Trage die fehlenden ganzzahligen Werte ein.
Das Schiff ist von Leuchtturm A , km und von Leuchtturm B , km weit entfernt.
richtig: 0falsch: 0
Aufgabe 50: Die Skizze unten gibt an, wie weit zwei Türme von einem Aussichtspunkt entfernt sind und in welchem Winkel die Messstrecken zueinander stehen. Wie weit sind die beiden Türme voneinander entfernt? Runde auf ganze Kilometer.
Die zwei Türme stehen km voneinander entfernt.
richtig: 0falsch: 0
Aufgabe 51: Berechne die Länge der Seite b. Trage das ganzzahlige Ergebnis unten ein.
b = , cm
richtig: 0falsch: 0
Aufgabe 52: |
Das durch die grüne Umrandung angedeutete gleichseitige Dreieck hat die Seitenlänge a = 10 cm. |
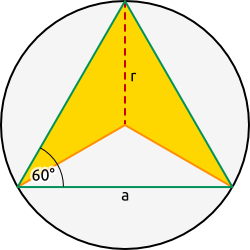
| a) Der Umkreis hat einen Radius von cm. b) Der gelbe Pfeil hat eine Fläche von cm². |
| Runde auf eine, rechne mit allen Nachkommastellen. |
richtig: 0falsch: 0
Aufgabe 53: Die Schenkellänge eines gleichschenkligen Dreiecks beträgt . Beide Schenkel bilden einen Winkel von . Wie lang ist die Basis dieses Dreiecks? Runde deinen Eintrag auf eine Nachkommastelle.
Die Basis ist cm lang.
richtig: 0falsch: 0
Aufgabe 54: Aus einem gleichschenkligen Dreieck wurde eine gleichschenklige Kerbe geschnitten, sodass der untere Pfeil entstand. Trage die fehlenden ganzzahligen Werte der jeweiligen Winkel ein.
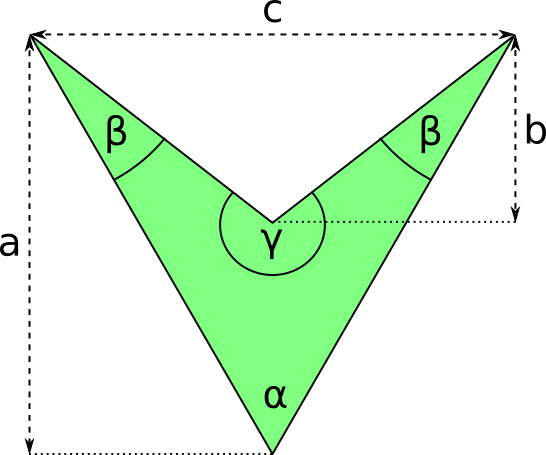
Skizze nicht maßstabsgetreu
α = ,° | β = ,° | γ = ,°
richtig: 0falsch: 0
Aufgabe 55: Trage unten den Flächeninhalt der beiden grünen Kreissegmente ein. Runde das Ergebnis auf eine Nachkommastelle.
A(grüne Kreissegmente) = cm²
richtig: 0falsch: 0
Aufgabe 56: Berechne den Flächeninhalt der gelben Fläche. Runde auf ganze Quadratzentimeter.
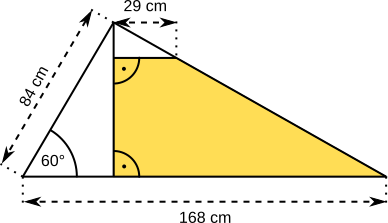
Der Flächeninhalt beträgt cm².
Versuche: 0
Aufgabe 57: Im gleichschenkligen Dreieck ABC gilt: ADreieck = 360 cm2 und h : tan58° = ![]() . Berechne den Umfang des Dreiecks. Runde auf eine Nachkommastelle.
. Berechne den Umfang des Dreiecks. Runde auf eine Nachkommastelle.
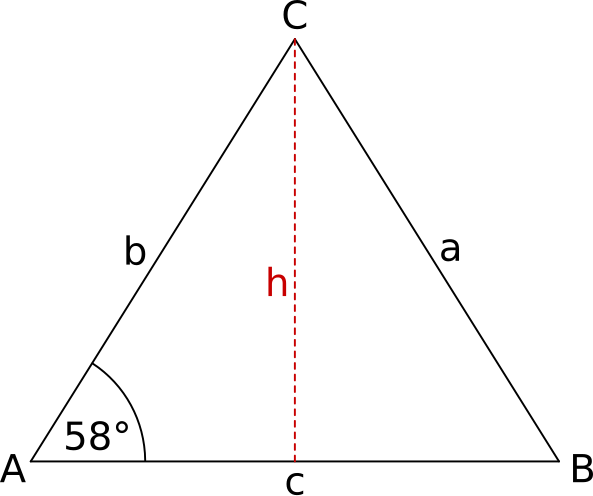
Der Umfang des Dreiecks beträgt cm.
Versuche: 0
Aufgabe 58: Der Bordcomputer eines Kleinflugzeuges, das in 800 m Höhe fliegt, berechnet anhand der in der Grafik aufgeführten Daten die Länge der Landebahn. Trage die Landebahnlänge unten ein. Runde auf Meter.
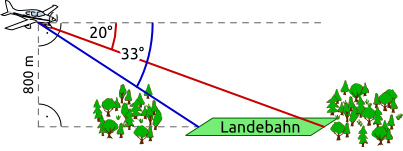
Die Landebahn ist m lang.
Versuche: 0
Aufgabe 59: Eine Turmspitze wird aus zwei Bodenpunkten (A: 25°, B: 48°) angepeilt, die 50 Meter voneinander entfernt sind. Trage die ganzzahlige Höhe des Turmes ein. Die Gleichungen helfen dir beim Rechnen.
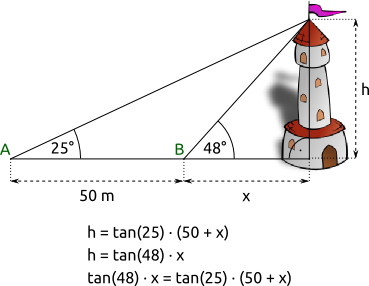 |
Der Turm ist ,19 m hoch.
Versuche: 0
Aufgabe 60: Aus einem über der Erde schwebendem Heißluftballon können zwei Personen das Zentrum ihrer Dörfer erkennen. Um Zentrum A zu sehen, müssen sie ihren Geradeausblick um nach unten senken. Zentrum B lässt sich in einem Winkel von anvisieren. Vom Erdboden aus gesehen, stehen die beiden Zentren in einem Winkel von . Wie weit sind die Dorfzentren voneinander entfernt? Runde auf eine Nachkommastelle.
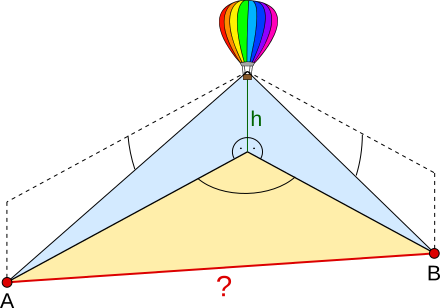
|
Die Dorfzentren sind km voneinander entfernt.
richtig: 0falsch: 0
Aufgabe 61: Der Flächeninhalt des unteren Dreiecks ABC wird folgendermaßen berechnet: A = 1 2 c · hc. Da die Höhe im rechten Winkel zu ihrer Grundseite steht, lässt sie sich auch mit dem Sinus eines Winkel bestimmen. Verschiebe die orangen Gleiter und versuche, die Logik der Tabelle nachzuvollziehen.
| A = 1 2 c · hc | |||
| α < 90° | α > 90° | β < 90° | β > 90° |
|
sin α =
hc
b
hc = b · sin α |
sin (180°-α) =
hc
b
hc = b · sin (180°-α) |
sin β =
hc
a
hc = a · sin β |
sin (180°-β) =
hc
a
hc = a · sin (180°-β) |
| sin α = sin (180° - α) | sin β = sin (180° - β) | ||
| hc = b · sin α | hc = a · sin β | ||
| A = 1 2 bc · sin α | A = 1 2 ac · sin β | ||
Den Flächeninhalt eines Dreiecks kann man berechnen, indem zwei seiner Seitenlängen und der Sinus des von ihnen eingeschlossen Winkels miteinander multipliziert werden. Die Hälfte dieses Produkts ist das gesuchte Ergebnis. Somit gilt auch: A = 1 2 ab · sin γ
Aufgabe 62: Berechne den Flächeninhalt der Dreiecke mit den unten aufgeführten Seitenlängen und Winkeln. Runde das Ergebnis auf eine Nachkommastelle.
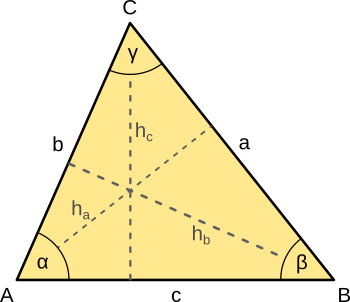
| a) a = 5cm, b = 5cm, γ = 5° | A = cm² |
| b) b = 5cm, c = 5cm, α = 5° | A = cm² |
| c) a = 5cm, c = 5cm, β = 5° | A = cm² |
richtig: 0falsch: 0
Aufgabe 63: Trage die Größen der Winkel ε und ζ ein. Runde auf ganze Gradangaben.
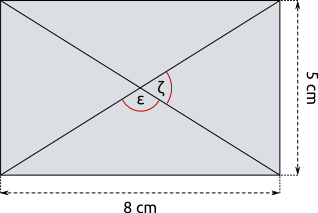
ε = ° ζ = °
Versuche: 0
Aufgabe 64: Trage den Winkel α des Trapezes ein. Runde auf ganze Gradangaben. Berechne anschließend den Umfang (u) und trage den ganzzahligen Teil davon ein.
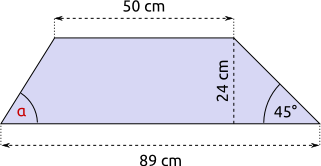
α = ° u = ,2 cm
Versuche: 0
Aufgabe 65: Trage den Flächeninhalt des gleichschenkligen Trapezes ein. Runde auf ganze Quadratzentimeter.

Das gleichschenklige Trapez hat eine Fläche von cm².
Versuche: 0
Aufgabe 66: Berechne beim gleichschenkligen Trapez den Flächeninhalt des roten Dreiecks. Runde auf eine Nachkommastelle.
A = cm²
richtig: 0falsch: 0
Aufgabe 67: Trage den Umfang der folgenden Figur in ganzen Zentimetern ein.

Der Umfang beträgt cm.
Versuche: 0
Aufgabe 68: Bei der unteren Figur sind das gleichschenklige Trapez ABCD und das rechtwinklige Dreieck ABE gegeben. Die Strecke AB = 24 cm und die Strecke CD = 16,5 cm. Wie lang ist die Strecke DE?
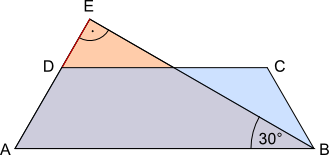
Die Strecke DE ist cm lang.
Versuche: 0
Aufgabe 69: In einem regelmäßigen Fünfeck ist eine Seite 8 cm lang. Welchen Flächeninhalt hat das Fünfeck? Runde auf ganze Quadratzentimeter.
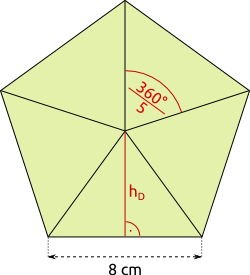
AFünfeck = cm²
Versuche: 0
Aufgabe 70: In welcher Höhe befindet sich der obere Rand folgender Arbeitsbühne? Runde auf Zentimeter.
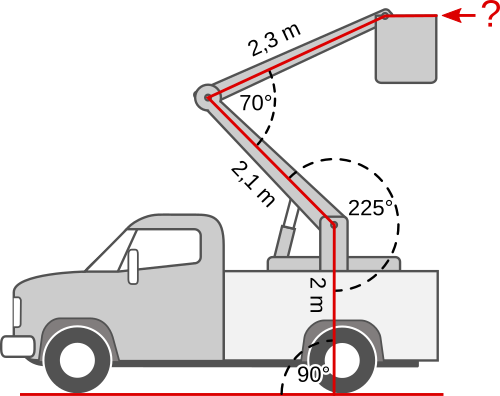
Der obere Rand befindet sich in Metern Höhe.
Versuche: 0
Aufgabe 71: Die Seite a des unteren Quadrates ist lang. Wie groß ist die grün markierte Fläche? Runde das Ergebnis auf eine Nachkommastelle.
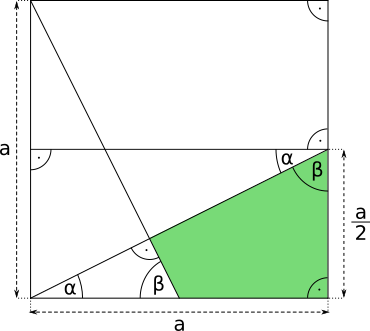
Der Flächeninhalt des grünen Vierecks beträgt cm2.
richtig: 0falsch: 0
Aufgabe 72: Trage den ganzzahligen Wert des Flächeninhaltes der unteren Figur ein. Die aufgeführten Zahlenwerte beziehen sich immer auf die dazugehörige Seitenlänge.
A = , cm²
richtig: 0falsch: 0
Aufgabe 73: Trage den ganzzahligen Wert des Flächeninhaltes der unteren Figur ein. Die aufgeführten Zahlenwerte beziehen sich immer auf die dazugehörige Seitenlänge.
A = , cm²
richtig: 0falsch: 0
Aufgabe 74: Wie groß ist beim folgenden Dreieck die Seite b und der Winkel γ? Runde die Ergebnisse auf eine Nachkommastelle.

b = cm | γ = °
Versuche: 0
Aufgabe 75: Eine quadratische Pyramide ist 220 m lang. Ihre Spitze wird 161 m von der Bodenkante entfernt in einem Winkel von 22° angepeilt. Wie hoch ist die Pyramide? Runde auf eine Nachkommastelle.
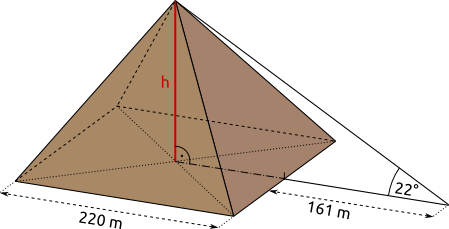
Die Pyramide hat eine Höhe von m.
Versuche: 0
Aufgabe 76: Die Sehne eines Betonkegels hat einen Winkel von 65° zur Grundfläche. Der Umfang des Kegels beträgt 3,78 m. Welche Höhe hat er? Runde auf Zentimeter.
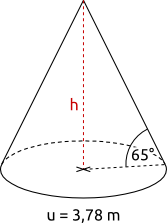
Der Kegel ist m hoch.
Versuche: 0
Aufgabe 77: Berechne a) das Volumen und b) den Oberflächeninhalt einer quadratischen Pyramide mit einer Parallelschnittfläche, die folgende Größen aufweist: und . Runde das Ergebnis auf ganze Kubik- und Quadratzentimeter.
| a) V = cm³ | b) O = cm² | |
|
|
Aufgabe 78: Trage den ganzzahligen Wert des Winkels α ein, der durch die Flächen- und die Raumdiagonale im Würfel gebildet wird. Mit dem Satz von Pythagoras kannst du die Längen der Diagonalen berechnen.
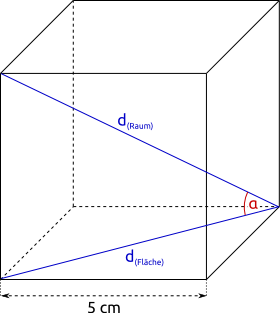
α = ,3°
Versuche: 0
Aufgabe 79: Berechne das Volumen des Quaders. Die Seite . Der Winkel und der Winkel . Runde auf ganze Kubikzentimeter.
Das Volumen des Quaders berägt cm3.
richtig: 0falsch: 0
Aufgabe 80: Trage die Länge der Dachschräge (x) des Turmes ein. Runde auf eine Nachkommastelle.

Die Schräge des Turmdaches hat eine Länge von m.
Versuche: 0
Aufgabe 81: Berechne den Umfang des blauen Dreiecks (ABC), des orangen Dreiecks (ABD) sowie die Winkel α und δ. Trage den jeweils fehlenden ganzzahligen Wert ein.
u(ABC) = , cm | u(ABD) = , cm
α = , ° | δ = , °
richtig: 0falsch: 0
Aufgabe 82: Unten siehst du eine regelmäßige sechsseitige Pyramide. Trage die Größe des markierten Winkel α ein. Runde auf eine Nachkommastelle.
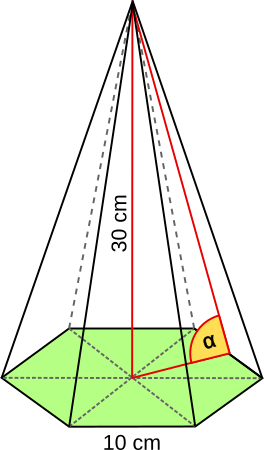
α = °
Versuche: 0
Aufgabe 83: Aus einer quadratischen Pappe mit der Seitenlänge wird der Mantel einer quadratischen Pyramide ausgeschnitten. Welches Volumen hat die Pyramide? Runde auf ganze Kubikzentimeter.
Die Pyramide hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 84: Das grüne Dreieck ABC liegt in einem regelmäßigen Sechseckprisma. Alle Prismaseiten haben eine Länge von . Trage den Flächeninhalt des Dreiecks unten ein. Runde das Ergebnis auf eine Nachkommastelle.
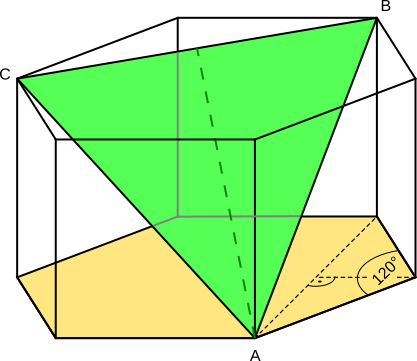
|
Das Dreieck hat eine Flächeninhalt von cm².
richtig: 0falsch: 0