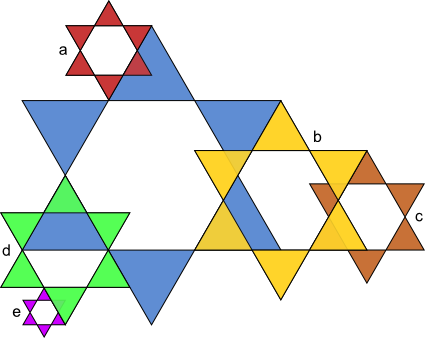
Ähnliche Figuren
Ähnliche Figuren stimmen in ihren Winkeln überein. Die einander zuordbaren Strecken (hier: rot ↔ rot, braun ↔ braun, blau ↔ blau, grün ↔ grün) stehen alle im gleichen Maßstab (k) zueinander.
| k = | Länge der Abbildstrecke |
| Länge der Originalstrecke |
Aufgabe 1: Ziehe an den Gleitern und beobachte, wie sich die Streckenlängen und Winkel jeweils verändern. Der quadratische Gleiter verändert den Maßstab (k) der Strecken.
Aufgabe 2: Ordne die Buchstaben der Flächen einander zu, die ähnlich sind.
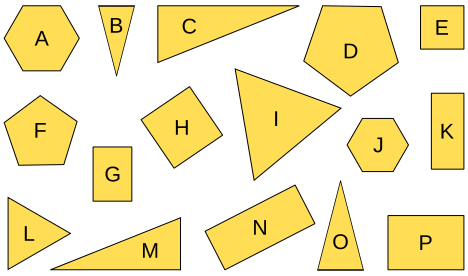
| A ~ | B ~ | C ~ | D ~ |
| E ~ | F ~ | G ~ | H ~ |
| I ~ | J ~ | K ~ | L ~ |
| M ~ | N ~ | O ~ | P ~ |
Versuche: 0
Aufgabe 3: Klick an, ob das untere Dreieck dem oberen ähnlich ist oder nicht.
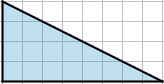
richtig: 0 | falsch: 0
Aufgabe 4: Klick alle Checkboxen unter den gelben Rechtecken an, die dem grünen Rechteck ähnlich sind.

| a) | b) | c) | d) | e) |
•: richtig | f: falsch | ↑: fehlende Markierung
richtig: 0 | falsch: 0
Aufgabe 5: Wenn die kurze rot Seite zur langen rot Seite im gleichen Verhältnis steht wie die kurze grüne Seite zur langen grünen Seite, dann sind die beiden rechtwinkligen Dreiecke ähnlich. Klick an, ob das rote und das gelbe Dreieck ähnlich sind oder nicht.
richtig: 0 | falsch: 0
Aufgabe 6: Ziehe die orangen Punkte so, dass ähnliche Figuren gleicher Farbe entstehen.
Versuche: 0
Maßstab (k)
Der Maßstab ist das Verhältnis zwischen der Länge der Abbildstrecke und der Länge der Originalstrecke. Er wird in verschiedenen Formen dargestellt:
|
→ | 1:2 |
|
→ | ½ |
|
→ | 0,5 |
Durch Formelumstellung lassen sich folgende Größen ermitteln.
- Maßstab = Abbildstrecke : Originalstrecke
- Abbildstrecke = Maßstab · Originalstrecke
- Originalstrecke = Abbildstrecke : Maßstab
Ist der Maßstab als Teilung oder Bruch angegeben, muss er bei der Berechnung der Originalstrecke in Klammern gesetzt werden.
- Beispiel: Abbildung 20 cm; Maßstab 2:5
Rechnung zum Original: 20 cm : (2:5) = 50 cm
Falsch: 20 cm :2 : 5= 2 cm
- Vergrößerung: Ist der Maßstab größer als 1, dann ist die Abbildung größer als das Original.
- Verkleinerung: Liegt der Maßstab zwischen 0 und 1, dann ist die Abbildung kleiner als das Original.
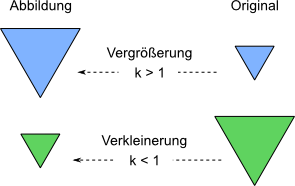
Aufgabe 7: Trage das Streckenverhältnis der grünen zur roten Linie ein
k = :
richtig: 0falsch: 0
Aufgabe 8: Die blaue Strecke a ist lang. Ziehe die rote Strecke a' am grünen Kreuz so, dass folgendes Streckenverhältnis entsteht:
| a' | = | |
| a |
richtig: 0 | falsch: 0
Aufgabe 9: Gib an, in welchem Maßstab die Strecken der Figuren vergrößert oder verkleinert wurden.
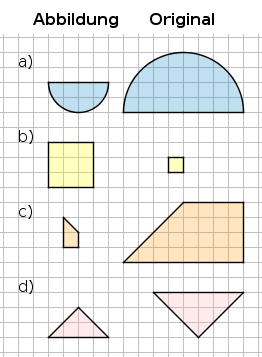 |
Maßstab
a) 1: b) :1 c) 1: d) 1: |
|
Versuche: 0 |
|
Aufgabe 10: Ergänze die fehlenden Werte in der Tabelle.
| a) | b) | c) | d) | e) | f) | |
| Maßstab (k) | 1:2 | 1:10 | 1: | 1:1000 | 1: | 1: |
| Abbildung | 3 cm | cm | 1 cm | 4 cm | 3 cm | 4 cm |
| Original | cm | 10 cm | 250 cm | cm | 15 cm | 120 cm |
Versuche: 0
Aufgabe 11: |
Trage die fehlenden Daten ein. |
|||||||
| zu a) |
Ist der Maßstab in der Form a:b aufgeführt, muss er im Taschenrechner umklammert werden. Beispiel: Abbildung 20 cm; Maßstab 2:5 Rechnung zum Original: 20 cm : (2:5) = 50 cm Falsch: 20 cm : |
|||||||
| zu c) |
Der Maßstab ist hier das gekürzte Verhältnis von Abbildung zu Original. Beispiel: Abbildung 20 cm; Original 50 cm
|
|||||||
| a) | Abbildung | Maßstab | Original (Abbildung : Maßstab) |
| Zei | (1:2) | cm | |
| b) | Maßstab | Original | Abbildung (Maßstab · Original) |
| 1:2 | Orig | cm | |
| c) | Abbildung | Original | Maßstab k (Abbildung : Original) |
| Zei | Orig | : | |
richtig: 0falsch: 0
Aufgabe 12: Ergänze die fehlenden Werte in der Tabelle.
| a) | b) | c) | d) | e) | f) | |
| Maßstab (k) | 2:1 | 10:1 | 1: | 1:25 | 1:500 | 1: |
| Abbildung | 16 dm | dm | 30 m | 2,2 m | km | 6 km |
| Original | dm | 0,1 dm | 240 m | m | 3500 km | 750 km |
Versuche: 0
Aufgabe 13: Eine Straßenkarte weist einen Maßstab von aus. Berechne die Strecke der Luftlinie zwischen zwei Städten, die auf der Karte auseinander liegen.
cm auf der Karte sind cm in der Wirklichkeit.
Umrechnung: cm = m = km.
richtig: 0falsch: 0
Aufgabe 14: Ergänze die fehlenden Werte in der Tabelle.
| a) | b) | c) | d) | e) | f) | |
| Maßstab (k) | 5:1 | 1:10 | 1: | 1:10000 | 1: | 1: |
| Abbildung | 75 cm | km | 0,6 dm | 1,5 cm | 3 cm | 2,5 cm |
| Original | cm | 30 km | 450 dm | m | 1,5 km | 0,5 km |
Versuche: 0
Aufgabe 15: Ergänze die fehlenden Werte in der Tabelle.
| a) | b) | c) | d) | e) | f) | |
| Maßstab (k) | 4:1 | 1:0,5 | 1: | 1:4,2 | 1:45000 | 1: |
| Abbildung | 7 m | dm | 6 cm | 5,5 m | m | 8 m |
| Original | m | 6,4 dm | 9 dm | m | 540 km | 96 km |
Versuche: 0
Aufgabe 16: Trage die richtigen Werte ein. Wenn der Cursor über den Maßstabsangaben steht, erscheint eine kleine Hilfe.
| Maßstab k |
Streckenlänge Abbildung |
Streckenlänge Original |
|||
| a) |
|
dm | |||
| b) | : | m | |||
| c) | cm | ||||
| d) | mm | ||||
| e) |
richtig: 0falsch: 0
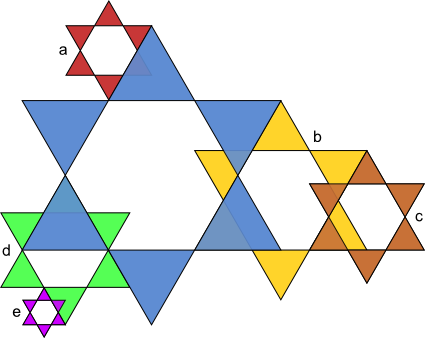
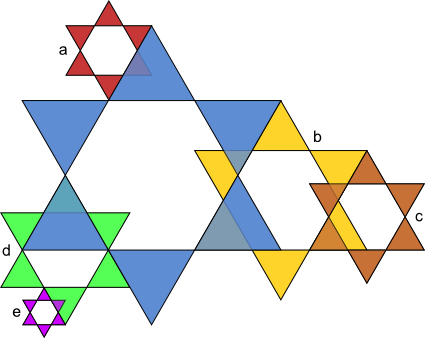
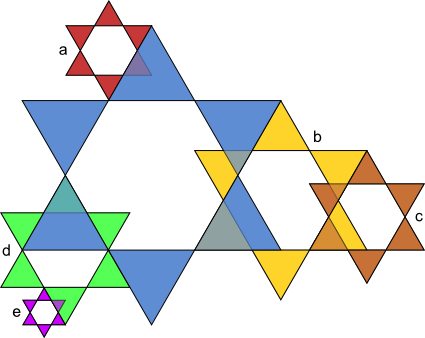
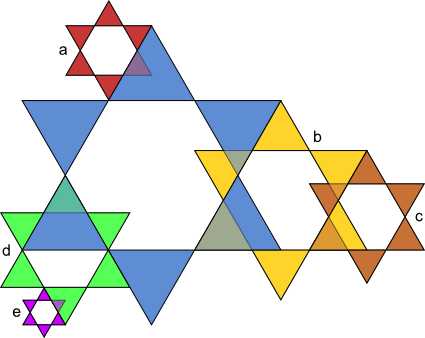
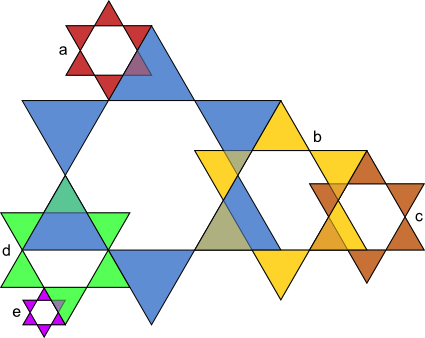
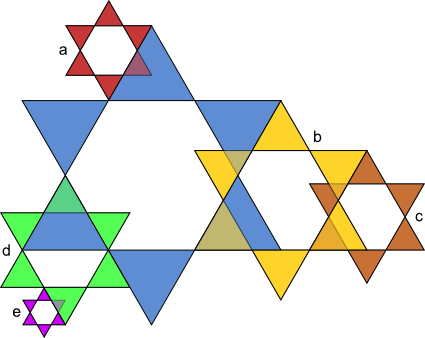
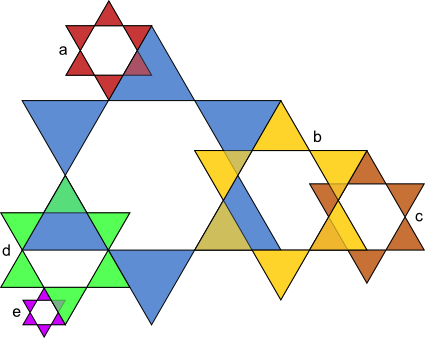
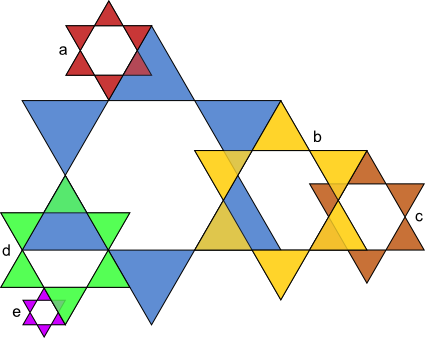
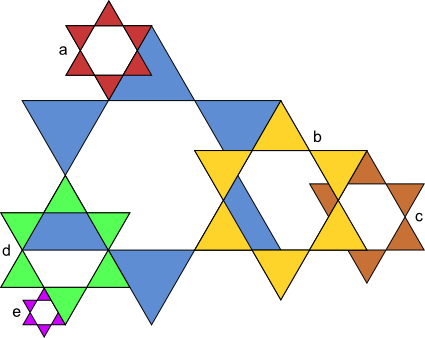
Aufgabe 17: Die kleinen Sterne sind Abbildungen des großen blauen Sterns. Mit welchem Maßstab wurden sie jeweils verkleinert? Kürze soweit wie möglich.
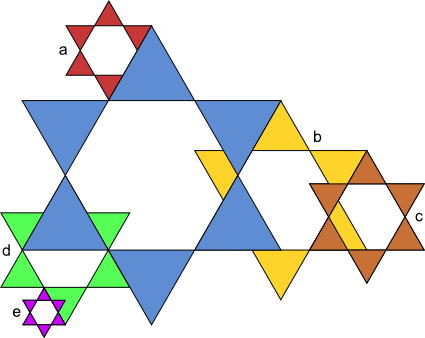
| k = a) | b) | c) | d) | e) | |||||
Versuche: 0
Aufgabe 18: Jana möchte ein maßstabsgetreues Modell von Sonne, Erde und Mond bauen. Als Erde verwendet sie einen Tischtennisball mit einem Durchmesser von 4 cm. Sie nimmt die Größen der folgenden Tabellen als Grundlage. Berechne die Größen des Modells und trage sie in die untere Tabellen ein. Achte auf die Maßeinheit und runde auf Zentimeter.
| Entfernung in Wirklichkeit | Durchmesser in Wirklichkeit | 
|
|||
| Sonne/Erde | 149 600 000 km | Sonne | 1 392 684 km | ||
| Erde/Mond | 384 400 km | Erde | 12 756 km | ||
| Mond | 3 476 km | ||||
| Entfernung im Modell | Durchmesser im Modell |
||||
| Sonne/Erde | m | Sonne | m | ||
| Erde/Mond | m | Erde | 4 cm | ||
| Mond | cm | ||||
Versuche: 0
Aufgabe 19: Das gelbe und das blaue Dreieck sind ähnlich. Berechne die Längen der Strecke x und y.
Angaben in cm
x = cm | y = cm
richtig: 0falsch: 0
Aufgabe 20: Ein Dreieck hat die Seitenlängen 14 cm, 48 cm und 50 cm. Ein ihm ähnliches Dreieck hat die Seitenlängen 72 cm und 75 cm. Wie lang ist die dritte Seite?
Antwort: Die dritte Seite ist cm lang.
Versuche: 0
Aufgabe 21: |
Ein 200 m langes und 60 m breites Grundstück wird auf einer Karte im Maßstab 1:800 dargestellt. |
| a) | Welche Länge und welche Breite hat das Rechteck auf der Karte? |
| b) | Welchen Flächeninhalt hat das Grundstück in der Realität und welchen auf der Karte? |
| c) | Welcher Maßstab trifft auf die Umrechnung der Fläche zu? |
| Antwort: | |
| a) | Das Rechteck hat auf der Karte eine Länge von cm und eine Breite von cm |
| b) | Das Grundstück hat in der Realität einen Flächeninhalt von m². Auf der Karte beträgt der Flächeninhalt cm². |
| c) | Der Flächenmaßstab beträgt 1: |
Versuche: 0
Aufgabe 22: Ein Rechteck hat einen Flächeninhalt von 32 cm2. Seine Seiten haben das Streckenverhältnis a b = 1 2 . Trage die Seitenlänge a und b ein.
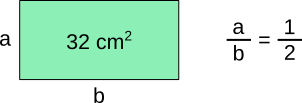
a = cm | b = cm
Versuche: 0