Zylinder 
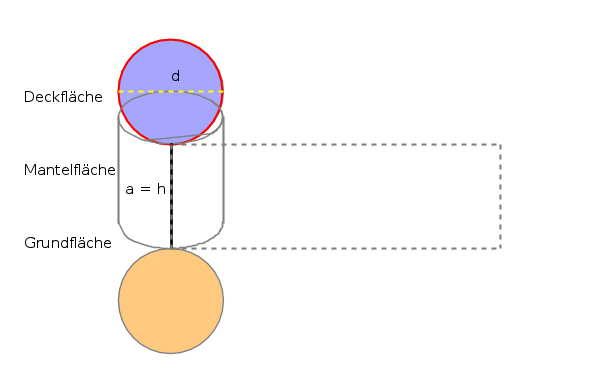
Ein Zylinder ist ein Körper, bei dem zwei gleichartige (kongruente) meist kreisrunde Grundflächen sich parallel gegenüberstehen und durch einen Mantel miteinander verbunden sind.
Anmerkung: Volumen und Oberflächeninhalt von Prisma und Zylinder werden faktisch nach gleichem Schema berechnet. Im Film wird in didaktischer Vereinfachung der Zylinder als Spezialfall eines Prismas mit unendlich vielen Ecken eingeordnet. Streng mathematisch gesehen ist ein Zylinder aber kein Prisma, da die Grundfläche eines Zylinders kein Polygon mit unendlich vielen Ecken sondern ein Kreis ohne Ecken ist.
![]()
 G. = Grundfläche Berechnung des Volumens (V) Das Zylindervolumen wird mit Grundfläche mal Höhe (V = G · h) berechnet. Da ein Kreis die Grundfläche eines Zylinders ist, wird die Kreisfläche (π · r²) mit der Höhe (h) des Zylinders multipliziert. V = π · r² · h Berechnung der Oberfläche (O) Der Grundflächenkreis eines Zylinders hat einen Umfang von π · d. Dieser Umfang bildet die untere Seite des abgewickelten Mantelrechtecks. Das Mantelrechteck hat die gleiche Höhe (h) wie der Zylinder. Die Mantelfläche berechnet sich demnach mit π · d · h. Zur Berechnung der gesamte Oberfläche werden die Grund- und die Deckfläche (2 · π · r²) noch hinzugefügt. M = π · d · h Aufgabe 1: Klick die richtigen Terme an. Formeln:
Versuche: 0 |
Aufgabe 2: Klick auf den "Auto"-Button und beobachte, wie der Zylindermantel entlang der Grundfläche so abgerollt werden kann, dass er ein Rechteck bildet.
© 2000 - http://geonext.de
 |
|||||
|
Volumen
Aufgabe 3: Klick das richtige Volumen des Zylinders unten an.
|
|
| Volumen = cm³ |
richtig: 0 | falsch: 0
Aufgabe 4: Berechne das Volumen des jeweiligen Zylinders. Runde auf ganze Kubikzentimeter.
| a) | r = cm | b) | d = cm |
| h = cm | h = cm | ||
| V = cm3 | V = cm3 |
richtig: 0falsch: 0
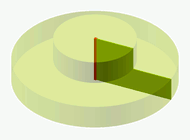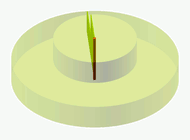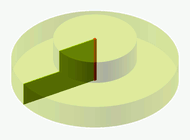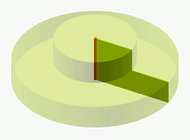
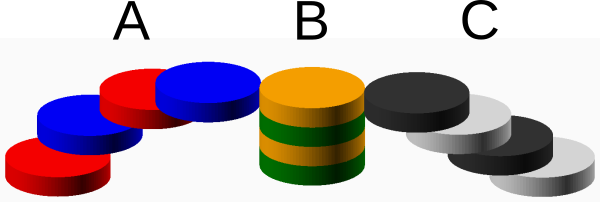
Aufgabe 5: Für die Wendeltreppe (A), den Zylinder (B) und die gerade Treppe (C) wurden die gleichen zylinderförmigen Sockel verwendet. Ordne die Volumen der jeweiligen Körper einander zu.
|
VA
VB
VC
VA
Versuche: 0 |
Aufgabe 6: Ein Rechteck hat die Maße a = 6 cm und b = 6 cm. Es wird um eine Seite gedreht. Wie groß ist das Volumen des entstehenden Drehkörpers? Runde auf ganze Kubikzentimeter.
a) Das Rechteck wird um Seite b gedreht. |
b) Das Rechteck wird um Seite a gedreht. |
|
 |
 |
|
| Die Zeichnung ist nicht maßstabsgetreu. | ||
| a) | Das um Seite b gedrehte Rechteck hat ein Volumen von cm3. |
| b) | Das um Seite a gedrehte Rechteck hat ein Volumen von cm3. |
richtig: 0falsch: 0
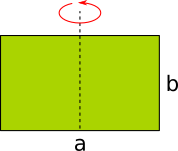
Aufgabe 7: Ein Rechteck hat die Maße a = 6 cm und b = 6 cm. Es wird um die Mitte einer Seite gedreht. Wie groß ist das Volumen des entstehenden Drehkörpers? Runde auf ganze Kubikzentimeter.
a) Das Rechteck wird um die Mitte der Seite a gedreht. |
b) Das Rechteck wird um die Mitte der Seite b gedreht. |
|
 |
 |
|
| Die Zeichnung ist nicht maßstabsgetreu. | ||
| a) | Das um die Mitte der Seite a gedrehte Rechteck hat ein Volumen von cm3. |
| b) | Das um die Mitte der Seite b gedrehte Rechteck hat ein Volumen von cm3. |
richtig: 0falsch: 0
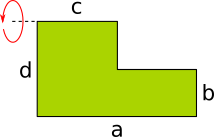
Aufgabe 8: Eine Figur aus zwei Rechtecken, die eine gemeinsam Gerade (a) aufweisen, hat die Maße a = 6 cm, b = 6, c = 6 cm und d = 6 cm. Die Figur wird um je eine der außenstehenden Seiten (d, c) gedreht. Wie groß ist das Volumen des entstehenden Drehkörpers? Runde auf ganze Kubikzentimeter.
a) Die Fläche wird um Seite d gedreht. |
b) Das Fläche wird um Seite c gedreht. |
|
 |
 |
|
| Die Zeichnung ist nicht maßstabsgetreu. | ||
| a) | Die um die Seite d gedrehte Figur hat ein Volumen von cm3. |
| b) | Die um die Seite c gedrehte Figur hat ein Volumen von cm3. |
richtig: 0falsch: 0
Aufgabe 9: Ein rechteckiger Papierstreifen mit den Seitenlängen a = und b = wird entlang der Seite a zu einem Kreis gebogen. Welches Volumen nimmt der so entstehende Zylinder ein? Trage den ganzzahligen Wert der Lösung ein.
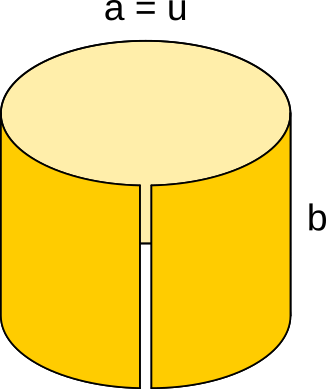
Das Volumen beträgt , cm3.
richtig: 0falsch: 0
Oberfläche
Aufgabe 10: Klick die richtige Oberfläche des Zylinders unten an.
|
|
| Oberfläche = cm² |
richtig: 0 | falsch: 0
Aufgabe 11: Berechne die Oberfläche des jeweiligen Zylinders. Runde auf ganze Quadratzentimeter.
| a) | r = cm | b) | d = cm |
| h = cm | h = cm | ||
| O = cm2 | O = cm2 |
richtig: 0falsch: 0
Aufgabe 12: Berechne die Mantelfläche des jeweiligen Zylinders. Runde auf ganze Quadratzentimeter.
| a) | r = cm | b) | d = cm |
| h = cm | h = cm | ||
| M = cm2 | M = cm2 |
richtig: 0falsch: 0
Oberfläche und Volumen
Aufgabe 13: Trage Oberfläche und Volumen der Zylinder ein. Runde auf eine Stelle nach dem Komma.
| a) |
r = cm h = cm O = cm² V = cm³ |
b) |
r = m h = m O = m² V = m³ |
c) |
r = mm h = mm O = mm² V = mm³ |
richtig: 0falsch: 0
Aufgabe 14: Berechne die Oberfläche und das Volumen der durch Grund- und Deckfläche halbierten Zylinder mit folgenden Maßen. Trage den ganzzahligen Betrag in die Textfelder ein.
a)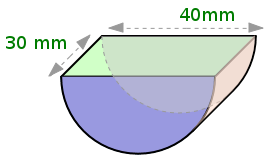 |
b)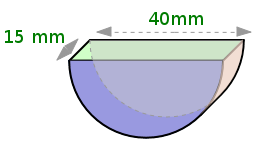 |
c)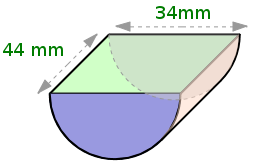 |
d)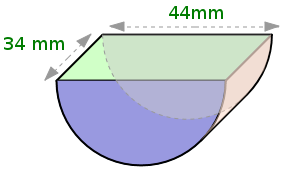 |
| a) | b) | c) | d) | |
| Durchmesser | 40 mm | 40 mm | 34 mm | 44 mm |
| Tiefe | 30 mm | 15 mm | 44 mm | 34 mm |
| Oberfläche | ,6 mm² | ,1 mm² | ,8 mm² | ,4 mm² |
| Volumen | ,6 mm³ | ,8 mm³ | ,2 mm³ | ,0 mm³ |
Versuche: 0
Aufgabe 15: Berechne Oberfläche und Volumen des folgenden Werkstücks. Runde auf ganze cm² (cm³).
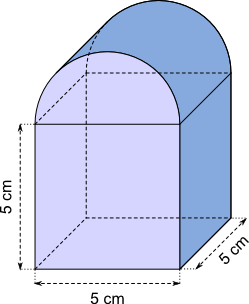
| a) Die Oberfläche des Werkstücks beträgt cm². |
| b) Das Volumen des Werkstücks beträgt cm³. |
Versuche: 0
Aufgabe 16: Berechne Oberfläche und Volumen des folgenden Werkstücks. Runde auf ganze mm² (mm³).
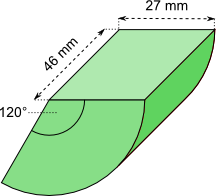
| a) Die Oberfläche des Werkstücks beträgt mm². |
| b) Das Volumen des Werkstücks beträgt mm³. |
Versuche: 0
Aufgabe 17: Berechne Oberfläche und Volumen des folgenden Werkstücks. Runde auf ganze cm² (cm³).
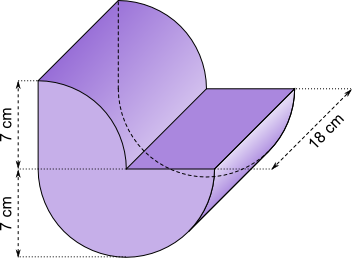
| a) Die Oberfläche des Werkstücks beträgt cm². |
| b) Das Volumen des Werkstücks beträgt cm³. |
Versuche: 0
Aufgabe 18: Berechne Oberfläche und Volumen des folgenden Werkstücks. Runde auf ganze mm² (mm³).
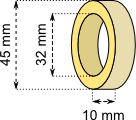
| a) Die Oberfläche des Ringes beträgt mm². |
| b) Das Volumen des Ringes beträgt mm³. |
Versuche: 0
Aufgabe 19: Berechne Oberfläche und Volumen des folgenden Werkstücks. Runde auf ganze cm² (cm³).
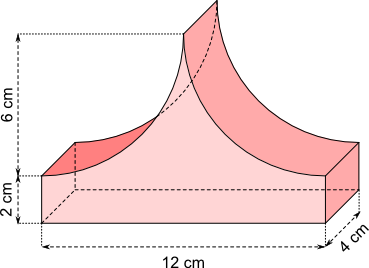
| a) Die Oberfläche des Werkstücks beträgt cm². |
| b) Das Volumen des Werkstücks beträgt cm³. |
Versuche: 0
Aufgabe 20: Berechne das Volumen des folgenden Werkstücks. Trage den ganzzahligen Wert der berechneten cm³ ein.
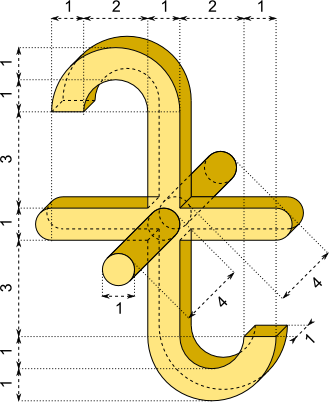
Maße in cm
Das Volumen des Werkstücks beträgt ,5 cm³.
Versuche: 0
Gemischte Größen
Aufgabe 21: Volumen und Radius oder Durchmesser sind gegeben. Berechne die Höhe des jeweiligen Zylinders. Runde auf ganze Zentimeter.
| a) | V = cm3 | b) | V = cm3 |
| r = cm | d = cm | ||
| h = cm | h = cm |
richtig: 0falsch: 0
Aufgabe 22: Volumen und Höhe sind gegeben. Berechne den Radius beziehungsweise den Durchmesser des jeweiligen Zylinders. Runde auf ganze Zentimeter.
| a) | V = cm3 | b) | V = cm3 |
| h = cm | h = cm | ||
| r = cm | d = cm |
richtig: 0falsch: 0
Aufgabe 23: Oberfläche und Radius oder Durchmesser sind gegeben. Berechne die Höhe des jeweiligen Zylinders. Runde auf ganze Zentimeter.
| a) | O = cm2 | b) | O = cm2 |
| r = cm | d = cm | ||
| h = cm | h = cm |
richtig: 0falsch: 0
Aufgabe 24: Die Mantelfläche und eine weitere Größe sind gegeben. Berechne die gesuchte Größe. Runde auf ganze Zentimeter.
| a) | M = cm2 | b) | M = cm2 |
| h = cm | d = cm | ||
| r = cm | h = cm |
richtig: 0falsch: 0
Aufgabe 25: Der Oberflächeninhalt eines Zylinders mit einem Radius von beträgt 113 cm². Wie groß ist die Mantelfläche? Trage den fehlenden ganzzahligen Wert unten ein.
Die Mantelfläche beträgt , cm².
richtig: 0falsch: 0
Aufgabe 26: Die Grundfläche eines hohen Zylinders ist groß. Berechne den Oberflächeninhalt. Trage den fehlenden ganzzahligen Wert unten ein.
Der Oberflächeninhalt beträgt , cm².
richtig: 0falsch: 0
Aufgabe 27: Trage unten die passenden Zahlen für die entsprechenden Größen eines Zylinders ein.
- Im gelben Bereich wird auf ganze Zahlen gerundet.
- Im blauen Bereich wird auf zwei Nachkommastellen gerundet.
| Radius r (cm) | xx | xx | |||
| Durchmesser d (cm) | xx | ||||
| Körperhöhe h (cm) | xx | xx | xx | ||
| Volumen V (cm³) | xx | xx | |||
| Mantelfläche M (cm²) | xx | xx | |||
| Oberfläche O (cm²) |
richtig: 0falsch: 0
Aufgabe 28: Trage unten in die Gleichung einen Radius (r) und eine Höhe (h) so ein, dass das Volumen (V) des Zylinders zwischen und cm³ liegt.
| G |
· | h | = | V |
| π · ² cm² | · | cm | = | cm³ |
richtig: 0 | falsch: 0
Aufgabe 29: Trage unten in die Gleichung einen Durchmesser (d) und eine Höhe (h) so ein, dass die Mantelfläche (M) des Zylinders zwischen und cm² liegt.
| d |
· π | · | h | = | M |
| cm | · π | · | cm | = | cm² |
richtig: 0 | falsch: 0
Sachaufgaben
Aufgabe 30: Zoltan will in seinem Garten einen Zylinder aus Zement mit einem Durchmesser von 38 Zentimetern und einer Höhe von 2,20 Metern anfertigen. Wie viele 25-kg-Säcke muss er kaufen, wenn der Zement eine Dichte von 1,2 kg pro Liter hat? Runde auf ganze Säcke.
Er benötigt Säcke Zement.
Versuche: 0
Aufgabe 31: |
Ein zylindrischer Messbecher hat einen Durchmesser von 7 cm und eine Höhe von 15 cm. |
| a) In den Messbecher passen cm³ Wasser. |
| b) Der Füllstrich für ½ Liter Wasser befindet sich in cm Höhe. |
Versuche: 0
Aufgabe 32: Eine ein Meter lange alukaschierte Rohrschale dämmt ein 18 mm breites Rohr mit einer 20 mm breiten Steinwollschicht. Die Aluminiumfolie überlappt sich am Öffnungsschlitz für einen ein Zentimeter breiten Klebestreifen. Wie viel Quadratmeter Aluminiumfolie werden für die Herstellung von 100 Rohrschalen benötigt? Runde auf eine Nachkommastelle.

Es werden m² Aluminiumfolie benötigt.
Versuche: 0
Aufgabe 33: Der Motor eines Lanz Bulldog konnte nicht einzylindrig genug sein. Der HL-Bulldog hatte eine Bohrung von 190 mm und einen Hub von 220 mm. Wie viel Liter Hubraum (durch Bohrung und Hub zur Verfügung stehender Platz) hatte dieser Motor? Runde auf eine Stelle nach dem Komma. Der Traktor hatte einen Hubraum von Liter. Versuche: 0 |
Bohrung | ||
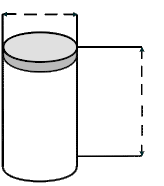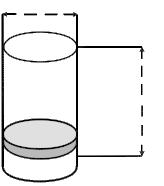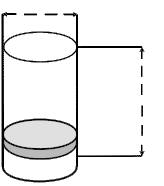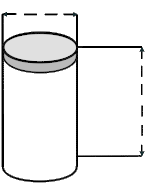 |
Hub | ||
Aufgabe 34: Hat ein Motor mehrere Zylinder, dann berechnet sich der Hubraum aus der Bohrung, dem Hub (s. Aufgabe 33) und der Anzahl der Zylinder. Trage die fehlenden Werte unten ein. Runde auf Hundertstel.
| Motor | Bohrung | Hub | Anzahl der Zylinder | Hubraum | 
|
| a) | 82 mm | 76 mm | 4 | cm³ | |
| b) | 76 mm | 86 mm | 8 | cm³ | |
| c) | 81 mm | 86 mm | 2215,79 cm³ | ||
Versuche: 0 |
|||||
Aufgabe 35: Ein zylindrischer Messbecher soll mit Messstrichen versehen werden. Der innere Durchmesser beträgt 7 cm. In welcher Höhe befindet sich der Füllstrich für 1 Liter? Runde auf Millimeter.

Die Ein-Liter-Markierung befindet sich in einer Höhe von cm.
Versuche: 0
Aufgabe 36: Ein Stahlrohr hat einen Außendurchmesser von 1676 mm und eine Wandstärke von 25 mm.Das Rohr ist 18,30 m lang. Ein Kubikdezimeter (dm3) Stahl wiegt 7,85 kg. Wie schwer ist das Rohr? Runde auf ganze Kilogramm.

Das Stahlrohr wiegt kg.
Versuche: 0
Aufgabe 37: Eine Konservendose mit einem Durchmesser von 99 mm und einer Höhe von 63 mm soll rundum mit einem Etikett versehen werden. Das Etikett soll oben und unten 5 mm vom Dosenrand entfernt sein. Trage die Fläche des Etiketts in cm² ein. Runde auf Zehntel.
Das Etikett hat eine Fläche von cm²
Versuche: 0
Aufgabe 38: Für eine Fußbodenheizung werden 80 m Rohr benötigt. Das Rohr hat einen Außendurchmesser von 20 mm und eine Wandstärke von 2 mm. Wie viel Liter Flüssigkeit werden benötigt, um dieses Rohr zu füllen? Runde auf ganze Liter.
Es werden Liter Flüssigkeit benötigt.
Versuche: 0
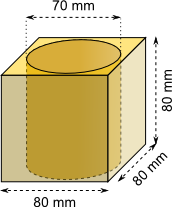
Aufgabe 39: Das Holz eines Buchenwürfels mit 80 mm Kantenlänge wiegt 0,7 g/cm³. Durch diesen Würfel wurde ein Loch mit 70 mm Durchmesser gebohrt. |
|
|
|
a) Wie schwer ist der gelochte Würfel? Runde auf ganze Gramm. |
||
Antwort: |
a) Der gelochte Würfel wiegt g |
|
|
Versuche: 0 |
||
Aufgabe 40: Durch einen 15 cm breiten Stahlwürfel wird mittig ein quadratischer Schlitz und von der anliegenden Seite ein kreisförmiges Loch gefräst. Der Schlitz hat eine Öffnung von 10 cm und das Loch einen Radius von 5 cm. Die Dichte von Stahl beträgt 7,86 g/cm³. Wie viel Kilogramm wiegt dieses Werkstück? Runde auf 2 Nachkommastellen.
Das Werkstück wiegt kg.
Versuche: 0
Aufgabe 41: Ein Türstopper besteht aus einem Metallzylinder und einem Gummiring. Trage die ganzzahligen Werte des Volumens der beiden Gegenstände ein.
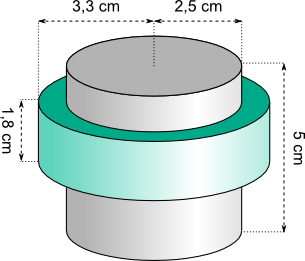
Der Metallzylinder hat ein Volumen von ,2 cm³. Der Gummiring hat ein Volumen von ,2 cm³.
Versuche: 0
Aufgabe 42: Welches Volumen hat ein Zylinder mit einer Höhe von 12,6 cm und einer Mantelfläche von 570 cm2? Runde auf ganze cm3.
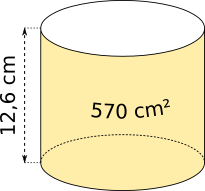
Der Zylinder hat ein Volumen von cm3.
Versuche: 0
Aufgabe 43: Ein Gussteil hat die Form eines Zylinders auf dem ein quaderförmiges Element aufgesetzt ist, das bündig mit der Zylinderrückwand abschließt. Welches Volumen hat dieses Gussteil? Runde auf ganze Kubikzentimeter.
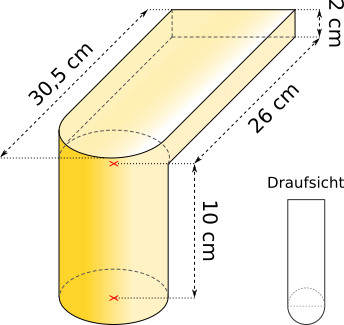
Das Gussteil hat ein Volumen von cm3.
Versuche: 0
Aufgabe 44: Ein Hantelhersteller entwickelt eine Kurzhantel die 5 kg wiegt. Der verwendete Stahl hat eine Dichte von 7,85 g/cm³. Die 5,5 cm dicken Seitenbacken sind zylindrisch und haben einen Durchmesser von 8 cm. Der Griff hat einen Durchmesser von 3 cm. Wie lang muss der Griff sein, damit die Hantel 5 kg wiegt? Runde auf Zehntel Zentimeter.
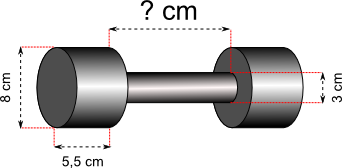
Der Griff muss zwischen den beiden Backen eine Länge von cm haben, damit die Hantel 5 kg wiegt.
Versuche: 0
Aufgabe 45: Es gibt Spinnenarten, die einen Faden von nur 0,0005 mm Durchmesser produzieren. Ein menschliches Haar hat einen Durchmesser von 0,1 mm. Wie viel Meter Spinnenfaden wird benötigt, um das Volumen von 10 cm Menschenhaar zu erhalten?
Um das Volumen von 10 cm Menschenhaar zu erhalten benötigt man m Spinnenfaden.
Versuche: 0
Aufgabe 46: In einer Gussform mit quadratischer Oberfläche befinden sich als Hohlraum zwei aneinander gefügte Viertelkreis-Segmente mit einem Radius von r = 5 cm. Der Hohlraum hat eine Höhe von 6 cm. Welches Volumen hat er? Runde auf eine Nachkommastelle.
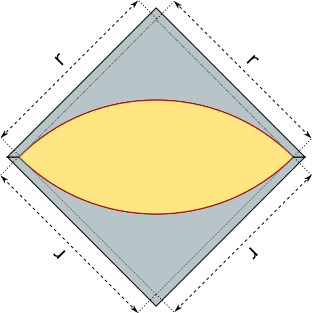
Der Hohlraum hat ein Volumen von cm3
richtig: 0 | falsch: 0