Trapez
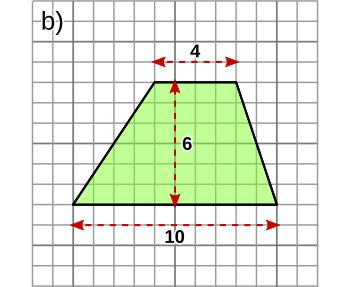
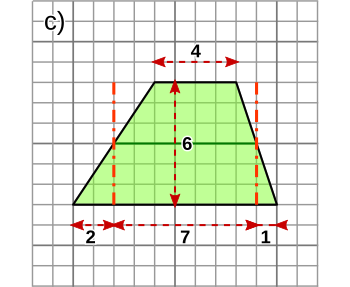
Ein Viereck mit mindestens einem paar paralleler Seiten heißt Trapez.
- Der Umfang des Trapezes ergibt sich aus der Summe der vier
Seitenlängen.
u = a + b + c + d. - Ein Trapez hat den gleichen Flächeninhalt wie ein Rechteck
mit der Länge der Trapezmittellinie (m) und der Trapezhöhe
(h). Die Mittellinie ist halb so lang wie die beiden
parallelen Trapezseiten zusammen. Die Fläche eines Trapezes
wird somit berechnet, indem die Längen der parallel zueinander
liegenden Linien zusammengezählt und dann durch zwei geteilt
werden. Das Ergebnis wird mit der Höhe Mal genommen.
A = a+c · h 2
Aufgabe 1: Bewege die orangen und roten Schieber der Grafik und beobachte, was passiert.
Aufgabe 2: Klick dich mit dem unteren, rechten Pfeil durch die Präsentation und ergründe, wie du ein Trapez in ein Rechteck umwandelst, um so die gemeinsame Fläche zu berechnen.
|
Start
|
|
|
|
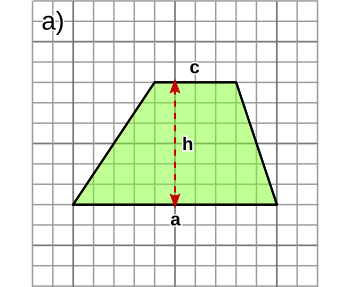
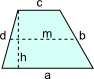
| Die parallelen Seiten eines Trapezes werden normalerweise mit a und c bezeichnet. Die Höhe mit h. | |
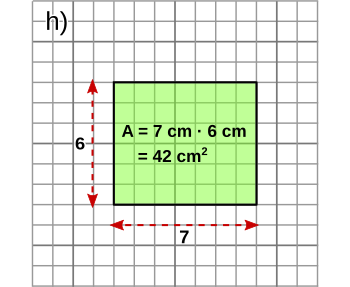
Aufgabe 3: Wandle das Trapez in ein Rechteck um und trage unten ihren Flächeninhalt ein. Ein Kästchen ist 1 cm2 groß.
Die Figur hat einen Flächeninhalt von cm2.
richtig: 0falsch: 0
Aufgabe 4: Berechne den Flächeninhalt des Trapezes.
Die Figur hat einen Flächeninhalt von cm2.
richtig: 0falsch: 0
Aufgabe 5: Trage den Flächeninhalt des Trapezes unten ein.
A = cm²
richtig: 0falsch: 0
Aufgabe 6: Bewege die Punkte auf die angegebenen Koordinaten und berechne den Flächeninhalt.
A(); B(); C(); D()
Der Flächeninhalt beträgt cm².
richtig: 0falsch: 0
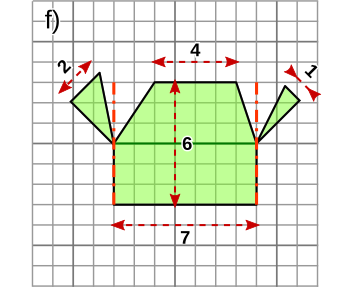
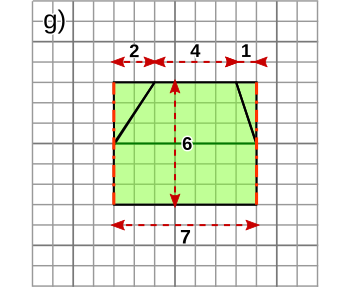
Aufgabe 7: Trage den Flächeninhalt der folgenden Figur unten ein.
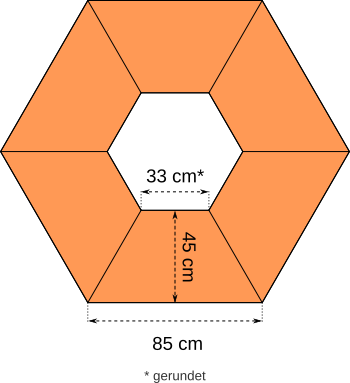
Die Figur hat einen Flächeninhalt von cm2.
Versuche: 0
Aufgabe 8: Trage unten in die Textfelder die fehlenden Größen ein.
richtig: 0falsch: 0
Aufgabe 9: Trage unten in die Textfelder die fehlenden Größen ein.
richtig: 0falsch: 0
Aufgabe 10: Die parallelen Seiten eines trapezförmigen Grundstücks (AB||CD) sind m voneinander entfernt. Sie haben eine Länge von m und m. Wie groß ist das Grundstück?
Das Grundstück hat eine Fläche von m².
richtig: 0falsch: 0
Aufgabe 11: Ein Trapez hat einen Flächeninhalt von cm². Die Seite a ist cm lang und die Seite c ist cm lang. Welche Höhe hat das Trapez über der Seite a?
Die Höhe über a beträgt cm.
richtig: 0falsch: 0
Aufgabe 12: Ein Trapez hat einen Flächeninhalt von cm². Die Seite a ist cm lang und die Höhe über a ist cm lang. Wie lang ist Seite c?
Die Seite a ist cm lang.
richtig: 0falsch: 0
Aufgabe 13: Ein trapezförmiger Garten hat eine Größe von 868 m². Auf der Mittelparallele liegt ein 2 m breiter Weg. Zu beiden Seiten hat er einen Abstand von 13 m zum Zaun. Am unteren Ende ist der Garten 43 m lang. Wie lang ist er am oberen Ende?
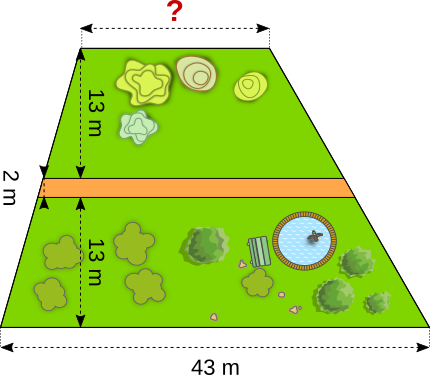
Am oberen Ende hat der Garten eine Länge von m.
Versuche: 0