Interaktive Formelsammlung
Alle Variablen können nach dem Anklicken durch Zahlen ersetzt werden.
Ein Klick auf die jeweilige Überschrift grenzt den Formelbereich ein.
Ähnlichkeitssätze |Bruch | Fläche | Funktion linear | Funktion quadratisch | Griechisches Alphabet | Grundrechenarten | Grundbegriffe d. Statistik | Klammern | Körper | Maßeinheiten | Potenz | Prozent, Promille | Pythagoras | Quadratische Gleichungen | Rechengesetze | Strahlensätze | Trigonometrie | Wachstumsprozesse | Wahrscheinlichkeit | Winkel | Zinsen (Formel) | Zinsen (Dreisatz)
Griechisches Alphabet
|
|
|
|
Grundrechenarten
Addition |
+ = |
| Summand + Summand = Summe | |
Subtraktion |
- = |
| Minuend - Subtrahend = Differenz | |
Multiplikation |
· = |
| Faktor 1 · Faktor 2 = Produkt | |
Division |
: = (b≠0) |
| Dividend : Divisor = Quotient | |
Potenzieren |
Radizieren |
|||||
|
=
ab → Potenz |
|
|||||
|
b√a → b-te Wurzel |
Rechengesetze
Kommutativgesetz |
|
+ = + |
|
· = · |
Assoziativgesetz |
|
+ ( + ) = ( + ) + |
|
· ( · ) = ( · ) · |
Distributivgesetz |
||||||||
|
· ( ± ) = · ± · |
||||||||
|
Bruch
Erweitern |
Kürzen |
||||||||||
|
|
||||||||||
| Zähler und Nenner mit gleicher Zahl multiplizieren |
Zähler und Nenner mit gleicher Zahl dividieren |
Addition b ≠ 0 |
Subtraktion b ≠ 0 |
||||||||||||||||
|
|
||||||||||||||||
|
|
Multiplikation |
Division b, c, d ≠ 0 |
||||||||||||||||||||||
|
|
||||||||||||||||||||||
|
Mit dem Kehrwert multiplizieren |
Klammern
Plusklammer auflösenZeichen bleiben erhalten |
| + (- + - ) = - + - |
Minusklammer auflösenZeichen ändern sich |
| - (- + - ) = + - + |
Ausmultiplizieren |
| · (- + - ) = - · + · - · |
Multiplizieren von Summen |
| ( + ) · ( - ) = · - · + · - · |
Potenz
Potenzieren |
|||||||||||||
| 1 = | 2 = · |
|
|||||||||||
| 0 = 1 (a≠0) | |||||||||||||
|
|
|
... | ||||||||||
Zehnerpotenz |
||
|
101 = 10 103 = 1 000 106 = 1 000 000 5 ·103 = 5000 |
10-1 = 0,1 10-3 = 0,001 10-6 = 0,000001 5 ·10-3 = 0,005 | |
Binomische Formeln (a ± b) · (a ± b) |
| ( + )² = ² + 2 · · + ² |
| ( - )² = ² - 2 · · + ² |
| ( + ) · ( - ) = ² - ² |
Potenzregeln |
() = · |
| · = + | · = ( · ) |
| : = - | : = ( : ) |
| Basis gleich | Exponent gleich |
Prozent, Promille
Prozent |
|||||||||||
Prozentwert
|
Prozentsatz
|
Grundwert
|
|||||||||
|
|||||||||||
Promille |
|||||||||||
Promillewert
|
Promillesatz
|
Grundwert
|
|||||||||
|
|||||||||||
Zinsen mit Dreisatz (Beispiel)
Im Bankwesen gilt: 1 Jahr hat 360 Tage; 1 Monat hat 30 Tage
|
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
Zinsen mit Formel
Im Bankwesen gilt: 1 Jahr hat 360 Tage; 1 Monat hat 30 Tage
Jahreszinsen |
|||||||||||
| Z = Zinsen | p = Zinssatz | K = Kapital | |||||||||
|
|
|
|||||||||
Monatszinsen |
m = Monate |
|
|
||||
|
|
Tageszinsen |
t = Tage |
|
|
||||
|
|
Zinseszins |
q=1+p:100 |
|
||||||||||||
| = 0 · |
|
|||||||||||||
|
|
Endwert |
Anfangswert |
|||
| = 0 · |
|
Wachstumsfak- |
Schrittanzahl |
||||||||||||
|
|
Winkelgrößen
spitzer Winkel0° < < 90°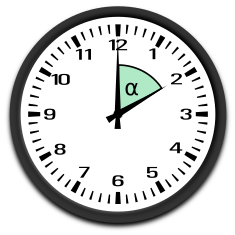
|
rechter Winkel= 90°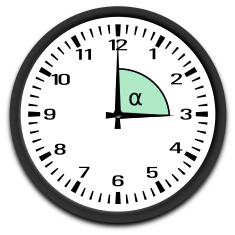
|
stumpfer Winkel90° < < 180°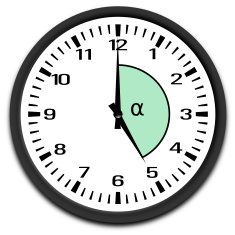
|
gestreckter Winkel= 180°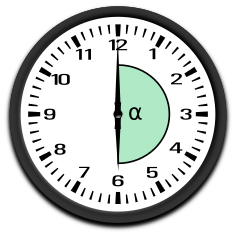
|
überstumpfer Winkel180° < < 360°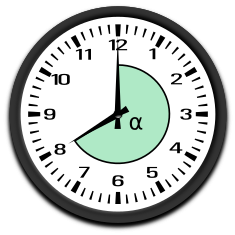
|
Vollwinkel= 360°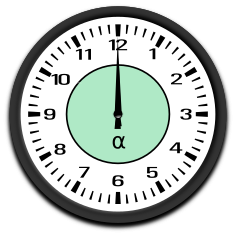
|
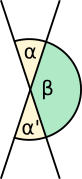
Winkel an sich schneidenden Geraden
Scheitelwinkel (α, α')= |
|
Nebenwinkel (α, β)+ = 180° |
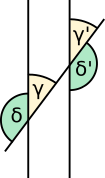
Stufenwinkel (γ, γ')= |
|
Wechselwinkel (δ, δ')= |
Winkelsummen
Winkelsumme Dreieck |
|
+ + = 180° 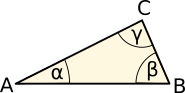
|
Winkelsumme Viereck |
|
+ + + = 360° 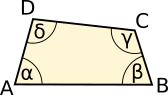
|
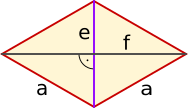
Drachen |
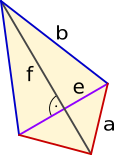
|
|||
= 2 · ( + ) |
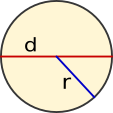
Kreisring |
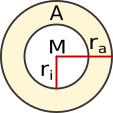 |
| = π · 2 - π · 2 | |
Kreissektor |
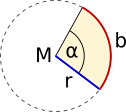
|
|||||||
|
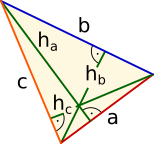
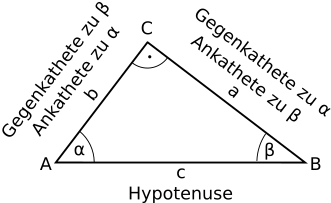
Pythagoras
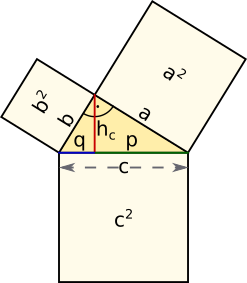
Satz des Pythagoras
|
² + ² = ² ² - ² = ² ² - ² = ² Wurzel ziehen! |
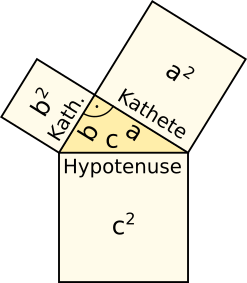
|
Höhensatz² = ·Kathetensatz² = ·² = · |
 |
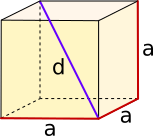
Würfel |
|
|
= · · = ³ = 6 · ² = · √3 |
Quader |
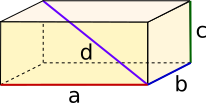 |
= · · |
|
| = 2 · ( · + · + · )
= √
² + ² + ² |
|
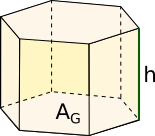
Prisma |
|
= · = 2 · + |
Zylinder |
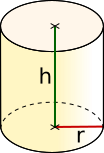
|
= π · ² · = 2 · π · · ( + ) = 2 · π · · |
Pyramide(quadratisch) |
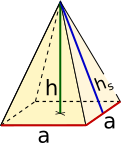
|
|||
= · ( + 2 · ) = 2 · · |
Kegel |
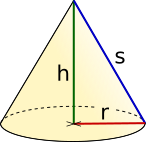
|
|||
= π · · ( + ) = π · · |
Kugel |
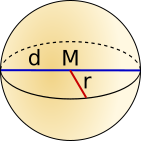
|
|||
= 4 · π · ² |
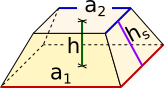 Pyramidenstumpf(quadratisch)= 2 · ( + ) · )
|
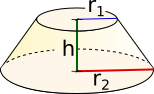 Kegelstumpf= π · · ( + )
|
Ähnlichkeitssätze
| Zwei Dreiecke sind ähnlich, wenn sie übereinstimmen ... | 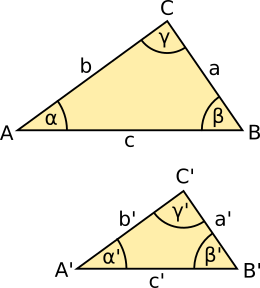 |
||
| • | in zwei Winkeln | = = | |
| • | in allen Verhältnissen entsprechender Seiten | : = : = : | |
| • | in einem Winkel und im Verhältnis der anliegenden Seiten | = : = : | |
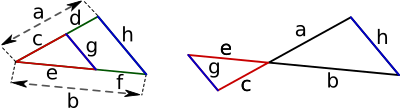
Strahlensätze
Erster Strahlensatz |
|||||||||||
|
|
||||||||||
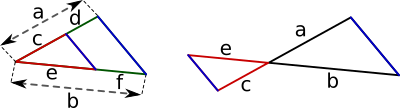
|
|||||||||||
Zweiter Strahlensatz |
|||||||||||
|
|
||||||||||
|
|||||||||||
Quadratische Gleichungen
Normalform |
² + + = 0 | |||||||||||
|
Lösungsformel
|
Lösungen: D > 0 → zwei D = 0 → eine D < 0 → keine |
Allgemeine Form |
² + + = 0 | ||||||||
|
|||||||||
Satz von Vieta |
|||||||
| Normalform | Allgemeine Form | ||||||
|
+ = - · = |
|
||||||
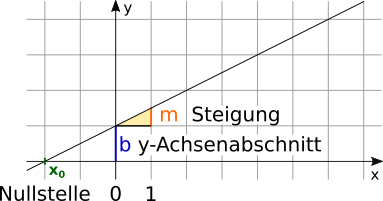
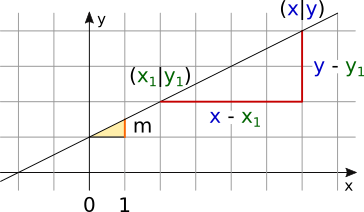
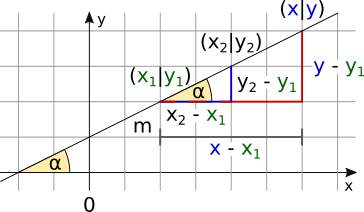
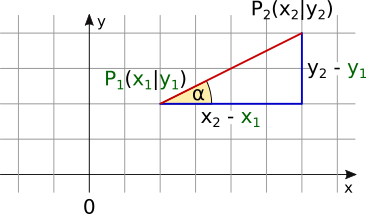
Lineare Funktion
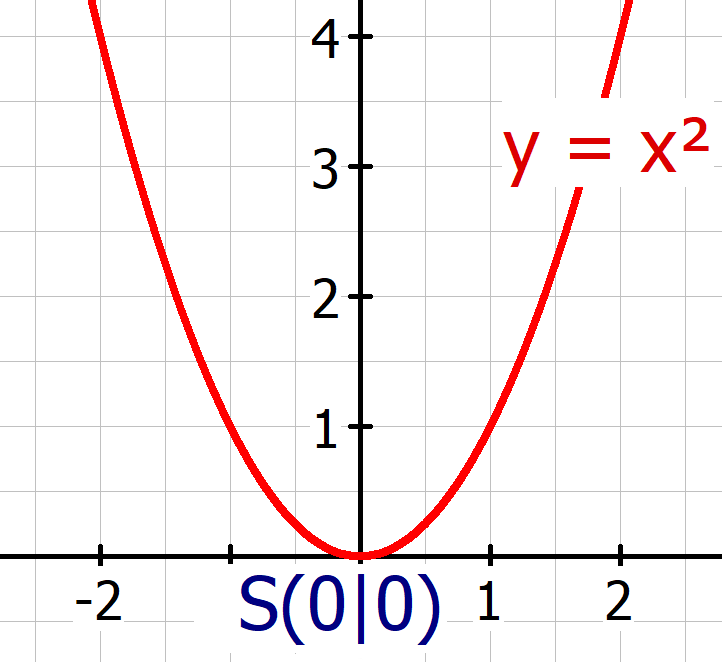
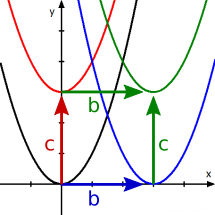
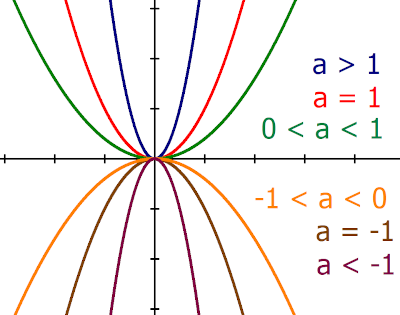
Quadratische Funktion
|
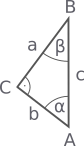
Sinus |
 |
||||||||||||
= sin ·
|
= sin ·
|
Kosinus |
 |
||||||||||||
= cos ·
|
= cos ·
|
Tangens |
 |
||||||||||||
= tan ·
|
= tan ·
|
Grundbegriffe der Statistik
|
|
Zentralwert z (Median)
mittlerer Wert der Rangliste Bei gerader Anzahl der
Mittelwert der beiden mittleren Werte |
||||||||||||||||||||||||
Wahrscheinlichkeit
Laplace-Experiment |
Beispiel: Würfel |
|||||||
| Ereignis E Kombinierte Ergebnisse |
||||||||
| Wahrscheinlichkeit P eines Ereignisses (E) |
|
|
||||||
| Gegenreignis E Alle ungünstigen Ereignisse |
P(E) = 1 - P(E) |
|
||||||
| Sicheres Ereignis | P(E) = 1 | P(• > 0) = 1 | ||||||
| unmögliches Ereignis | P(E) = 0 | P(• < 0) = 0 | ||||||
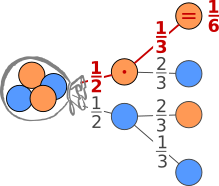
Produktregel |
P(2 x orange) |
Ereignisses ist gleich
dem Produkt der
Wahrscheinlichkeiten
längs des Pfades, der
zum Ergebnis führt.
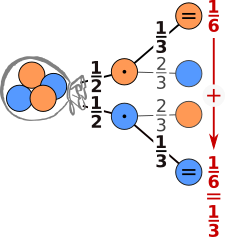
Summenregel P(2 x gleichfarbig)
eines Ereignisses ist
gleich der Summe
der Wahrscheinlichkeiten
aller Pfade, die für dieses Ereignis
günstig sind.
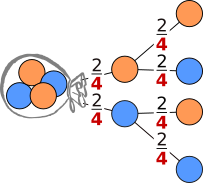
Ziehen mit zurücklegen
gezogen und wieder
zurückgelegt.
Der Nenner bleibt gleich.
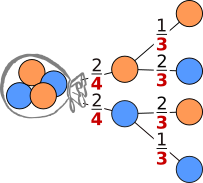
Ziehen ohne zurücklegen
gezogen und nicht
zurückgelegt.
Der Nenner wird um 1 kleiner.
Maßeinheiten
|
|||||||||||
| 1 km | = | 1000 m | → | 1 m | = | 0,001 km | |||||
| 1 m | = | 10 dm | → | 1 dm | = | 0,1 m | |||||
| 1 dm | = | 10 cm | → | 1 cm | = | 0,1 dm | |||||
| 1 cm | = | 10 mm | → | 1 mm | = | 0,1 cm | |||||
|
|||||||||||
| 1 km² | = | 100 ha | → | 1 ha | = | 0,01 km² | |||||
| 1 ha | = | 100 a | → | 1 a | = | 0,01 ha | |||||
| 1 a | = | 100 m² | → | 1 m² | = | 0,01 a | |||||
| 1 m² | = | 100 dm² | → | 1 dm² | = | 0,01 m² | |||||
| 1 dm² | = | 100 cm² | → | 1 cm² | = | 0,01 dm² | |||||
| 1 cm² | = | 100 mm² | → | 1 mm² | = | 0,01 cm² | |||||
|
|||||||||||
| 1 km³ | = | 1 000 000 000 m³ ↓ | |||||||||
| 1 m³ = 0,000 000 001 km³ | |||||||||||
| 1 m³ | = | 1000 dm³ | → | 1 dm³ | = | 0,001 m³ | |||||
| 1 dm³ | = | 1000 cm³ | → | 1 cm³ | = | 0,001 dm³ | |||||
| 1 cm³ | = | 1000 mm³ | → | 1 mm³ | = | 0,001 cm³ | |||||
|
|||||||||||
| 1 hl | = | 100 l | → | 1 l | = | 0,01 hl | |||||
| 1 l | = | 1000 ml | → | 1 ml | = | 0,001 l | |||||
| 1 l | = | 1 dm³ | 1 ml | = | 1 cm³ | ||||||
|
|||||||||||
| 1 t | = | 1000 kg | → | 1 kg | = | 0,001 t | |||||
| 1 kg | = | 1000 g | → | 1 g | = | 0,001 kg | |||||
| 1 g | = | 1000 mg | → | 1 mg | = | 0,001 g | |||||
|
|||||||||||
| 1 Jahr | = | 365 Tage | |||||||||
| 1 Tag | = | 24 h | → | 1 h | ≈ | 0,0417 Tage | |||||
| 1 h | = | 60 min | → | 1 min | ≈ | 0,0167 h | |||||
| 1 min | = | 60 s | → | 1 s | ≈ | 0,0167 min | |||||
Geschwindigkeit |
||||||||||||||||||
|