Binomische Formeln 
Binome sind zweigliedrige Terme. Sie haben die Form (a + b) oder (a - b). Beim Multiplizieren und Potenzieren unterscheidet man drei binomische Formeln.
| 1. binomische Formel: (a + b)² = a² + 2ab + b² → (a + b)2 | = | (a | + | b) | · | (a | + | b) |
| = | a · a | + | a · b | + | a · b | + | b · b | |
| = | a2 | + | 2ab | + | b2 | |||
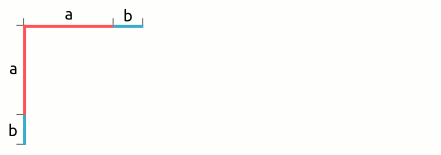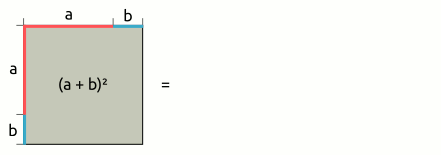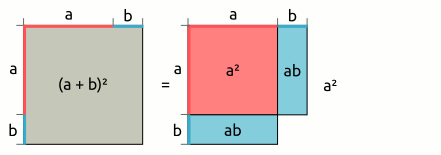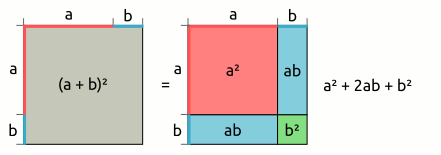 |
Grafik ausblenden. |
| 2. binomische Formel: (a - b)² = a² - 2ab + b² → (a - b)2 | = | (a | - | b) | · | (a | - | b) |
| = | a · a | + | a · (-b) | + | a · (-b) | + | (-b) · (-b) | |
| = | a2 | - | 2ab | + | b2 | |||
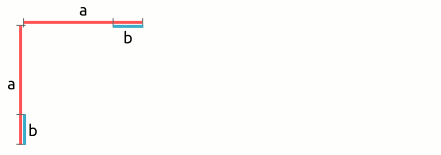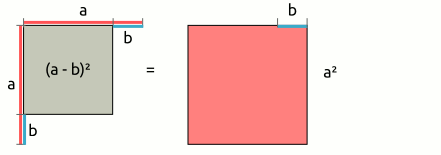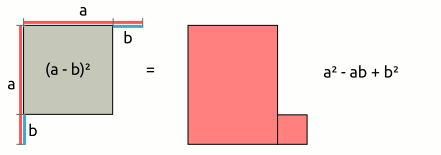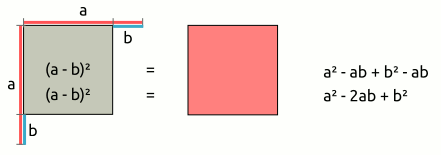 |
Grafik ausblenden. |
| 3. binomische Formel: (a + b) · (a - b) = a² - b² → | (a | + | b) | · | (a | - | b) | |
| = | a · a | + | a · (-b) | + | a · b | + | b · (-b) | |
| = | a2 | + | 0 | - | b2 | |||
 |
Grafik ausblenden. |
Aufgabe 1: Klick die richtigen Daten an.
|
a) (a + b)² = () · () = a² 2ab b² b) (a - b)² = () · () = a² 2ab b² c) () · (a - b) = a² b² Versuche: 0 |
Aufgabe 2: Trage die potenzierten Werte ein.
|
a) ( + x)² = + x + x² b) (y - )² = y² - y + c) ( + z) · ( - z) = - z² |
richtig: 0falsch: 0
Aufgabe 3: Trage die fehlenden Werte ein.
|
a) (6 + x)² = + x + x² b) (y - 7)² = y² - y + c) ( + z) · ( - z) = 25 - z² |
richtig: 0falsch: 0
Aufgabe 4: Klick zu den links stehenden Termen den richtigen rechten Lösungsbuchstaben im Aufklapp-Menü an.
| a) | b) | |
Aufgabe 5: Trage die richtigen Rechenzeichen ein.
|
a) (2 + e)² = 4 4e e² b) (9 - f)² = 81 18f f² c) (7 a)² = 49 - 14a + a² d) (10 b)² = 100 + 20b + b² e) (3x 2) · (3x + 2) = 9x² - 4 f) (12 5m) · (12 - 5m) = 144 - 25m² |
Versuche: 0
Aufgabe 6: Ergänze die Terme richtig.
|
a) = ()2 b) = ()2 c) = ()2 d) = ()2 |
richtig: 0falsch: 0
Aufgabe 7: Ergänze die Terme richtig.
|
a) v² - 25 = ( + ) · () b) 144 - w² = ( - ) · () |
Versuche: 0
Aufgabe 8: Ergänze die Terme richtig.
|
a) = ()2 b) = ()2 c) = ()2 d) = ()2 |
richtig: 0falsch: 0
Aufgabe 9: Ergänze die Terme richtig.
|
a) z² + 12z + ()² = ()² b) q² - 14q + ()² = ()² |
Versuche: 0
Aufgabe 10: Trage die richtigen Werte ein.
|
a) a² + 16a + ()² = (a + )² b) x² + 10x + = (x + )² c) 36 + 12 + ()² = (6 + v)² d) 144 + 24b + b² = ( + b)² |
Versuche: 0
Aufgabe 11: Trage die richtigen Werte ein.
|
a) a² - a + = (a - )² b) b² - b + = (b - )² c) x² + x + = (x + )² d) + y + y² = ( + y)² |
richtig: 0falsch: 0
Aufgabe 12: Löse die Klammern schriftlich auf. Trage dann die richtigen Werte ein.
|
a) ()2 = a2 + a + b) ()2 = - b + b2 |
richtig: 0falsch: 0
Aufgabe 13: Löse die Klammern schriftlich auf. Trage dann die richtigen Werte ein.
|
a) ()2 = a2 + a + b) ()2 = - b + b2 |
richtig: 0falsch: 0
Aufgabe 14: Löse die Klammern schriftlich auf. Trage dann die richtigen Werte ein.
|
|||||||||||||
|
richtig: 0falsch: 0
Aufgabe 15: Klammere mit Hilfe der binomischen Formeln schriftlich aus. Trage dann in die Gleichung die fehlenden Werte ein.
|
a) 2a2 + 4ab + 2b2 = · ( + b)2 b) 12x2 + 36xy + 27y2 = · (x + )2 |
Versuche: 0
Aufgabe 16: Klammere mit Hilfe der binomischen Formeln schriftlich aus. Trage dann in die Gleichung die fehlenden Werte ein.
a2 + ab + b2 = (a + b)2
richtig: 0falsch: 0
Aufgabe 17: Die Seiten des grünen Quadrates werden verlängert. Die neu entstandene gelbe Fläche hat einen Flächeninhalt von 6 cm2. Welchen Flächeninhalt hat das grüne Quadrat?
|
| b |
||
| x | x2 = ? | |
| x | ||
Gleichung: (x + )2 = x2 +
Das grüne Quadrat hat einen Flächeninhalt von cm2.
richtig: 0falsch: 0

