Zinseszins berechnen
Hebt man die Jahreszinsen eines Guthabens nicht ab, werden sie im Folgejahr dem Konto gutgeschrieben. Ab diesem Zeitpunkt werden sie mitverzinst. Der Zins dieser Zinsen ist der Zinseszins.
Aufgabe 1: Verändere die Vorgabewerte der Beispielrechnung und beobachte, wie sich das Guthaben (Kapital) und der entsprechende Zins von Jahr zu Jahr verändert.
Kapital: € || Zinssatz: % || Laufzeit: 5 Jahre
| 1. Jahr | K0 | |||
| Z1 | + | |||
| 2. Jahr | K1 | |||
| Z2 | + | |||
| 3. Jahr | K2 | |||
| Z3 | + | |||
| 4. Jahr | K3 | |||
| Z4 | + | |||
| 5. Jahr | K4 | |||
| Z5 | + | |||
| Endbetrag | K5 | |||
Die Zinsformel, mit der man aus dem Anfangskapital K0 bei einem vorgegebenen Prozentsatz p nach n Jahren das Endkapital Kn berechnen kann lautet:
Kn = K0 · qn
| q = 1 + | p |
| 100 |
Aufgabe 2: Ein Kapital von € wird Jahre lang mit einem festen Zinssatz von % verzinst. Die Zinsen werden mitverzinst. Berechne das Kapital am Ende des Jahres. Trage den ganzzahligen Wert des Endguthabens ein. Nach der fünften falschen Eingabe wird die Lösung angezeigt.
Das Kapital am Ende des Jahres beträgt €.
richtig: 0falsch: 0
Aufgabe 3: Trage das ganzzahlige Endkapital ein. Die Zinsen bleiben auf dem Konto.
| Anfangs kapital |
Zins- satz |
Zeit | End- kapital |
| € | |||
| € | |||
| € |
richtig: 0falsch: 0
Aufgabe 4: Nach wie vielen Jahren hat sich bei einem Zinssatz von 3 %, 3,5 % und 4 % ein Kapital verdoppelt? Trage die Jahreszahl ein, nach der der doppelte Wert überschritten wird.
Das Kapital hat sich bei einem Zinssatz von 3 % nach Jahren, bei einem Zinssatz von 3,5 % nach Jahren und bei einem Zinssatz von 4 % nach Jahren verdoppelt.
Versuche: 0
Durch das Umformen der Zinsformel (s.o.) können auch der Anfangswert K0 und der Zinsfaktor q bestimmt werden. Aus dem Zinsfaktor lässt sich der Zinssatz p erschließen.
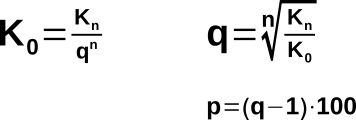
Aufgabe 5: Welchen Betrag müsste Herr Xaver heute anlegen, wenn er nach Jahren bei einem Zinssatz von % über annähernd € verfügen will? Trage den fehlenden ganzzahligen Betrag ein.
Er müsste einen Betrag von , € anlegen.
richtig: 0falsch: 0
Aufgabe 6: Hans kauft sich beim Gebrauchtwagenhändler für ein Auto, dass in den letzten jährlich an Wert verlor. Was hat das Auto vor gekostet? Runde auf Tausender.
Der Wagen kostete damals €.
richtig: 0falsch: 0
Aufgabe 7: Vor Jahren legte Herr Demir ein Kapital von € an. Der Zinssatz blieb in dieser Zeit konstant. Das heutige Kapital beträgt €. Mit wie viel Prozent war der Betrag verzinst? Runde auf eine Nachkommastelle.
Der Zinssatz betrug %.
richtig: 0falsch: 0
Aufgabe 8: Frau Maier legt bei der Bank einen Betrag von € auf Jahre bei gleichbleibenden Zinssatz an. Die Zinsen werden mitverzinst. Insgesamt erhält sie in den Jahren Zinsen im Wert von €. Welchen Zinssatz gewährte die Bank? Runde auf eine Nachkommastelle.
Die Bank gewährte einen Zinssatz von %.
richtig: 0falsch: 0
Aufgabe 9: Trage die fehlenden Werte ein. Am unteren Teil der Tabelle ist angegeben, auf wie viele Nachkommastellen das Ergebnis gerundet werden soll.
| Anfangs kapital |
Zins- satz |
Lauf -zeit |
Zinsen | End- kapital |
| € | € | |||
| € | € | |||
| % | € | |||
| % | € | |||
| Jahre | € | |||
| 0 | 1 | 0 | 2 | |
| ↑ Anzahl der einzutragenden Nachkommastellen ↑ | ||||
richtig: 0falsch: 0
Zuwachssparen
Beim Zuwachssparen steigt der Zinssatz von Jahr zu Jahr an. Die Zinsen werden mitverzinst. Hier wird das Anfangskapital mit dem entsprechenden Zinsfaktor eines jeden Jahres multipliziert.
| Beispiel Anfangskapital: 10 000 € |
||
| Zinssatz | Wertsteigerung | Zinsfaktor |
| 1. Jahr: 2,5 % | 102,5 % | 1,025 |
| 2. Jahr: 3,0 % | 103,0 % | 1,035 |
| 3. Jahr: 3,5 % | 103,5 % | 1,035 |
| Endkapital: 10 000 · 1,025 · 1,03 · 1,035 = 10 927,01 € | ||
Aufgabe 10: Auf wieviel Euro wächst ein Kapital von 50 000 € an, wenn die Zinsen
- im ersten Jahr 2 %,
- im zweiten Jahr 3 % und
- im dritten Jahr 4 % betragen?
Nach drei Jahren ist das Kapital auf € angewachsen.
Versuche: 0
Aufgabe 11: Lea legt bei ihrer Bank zu den angegebenen Zinsen auf drei Jahre an. Die Zinsen werden mitverzinst. Wie hoch ist ihr Kapital nach drei Jahren? Trage den ganzzahligen Wert des Endguthabens ein. Nach der fünften falschen Eingabe wird die Lösung angezeigt.
1. Jahr:
2. Jahr:
3. Jahr:
Nach drei Jahren hat Lea € auf dem Konto.
richtig: 0falsch: 0
Aufgabe 12: | Frau Schiefer legt 8 000 € an und erhält nach dem ersten Jahr 200 € Zinsen. |
| a) Der Zinssatz des ersten Jahres beträgt %.
b) Nach dem zweiten Jahr ist das Kapital auf € angewachsen. |
Versuche: 0
Ratensparen
Von Ratensparen spricht man, wenn eine jährlich eingezahlte Rate (z.B. 500 €) mit einem gleich bleibenden Zinssatz (z.B. 2 %) verzinst wird. Das Kapital nach 3 Jahren kann folgendermaßen berechnet werden:
| Jahr | 0 | 1 | 2 | 3 | Kurzform | |||
| Rate 1 | 500 € | · 1,02 | · 1,02 | · 1,02 | 500 € · 1,023 | |||
| Rate 2 | 500 € | · 1,02 | · 1,02 | + | 500 € · 1,022 | |||
| Rate 3 | 500 € | · 1,02 | + | 500 € · 1,021 | ||||
| Kapital nach 3 Jahren: |
|
|||||||
Allgemein lässt sich die Formel für das Ratensparen in folgende Formel zusammenfassen:
Kn = K0 · (qn + qn-1 + qn-2 ··· + q1)
K = Kapital, q = Zinsfaktor, n = Zeitintervall
Aufgabe 13: Frau Schatz schließt einen Ratensparvertrag ab. Jeweils zu Jahresbeginn zahlt sie ein. Der Zinssatz beträgt . Die Zinsen werden mitverzinst. Wie hoch ist das Guthaben nach Ablauf von ? Trage den ganzzahligen Wert des Endguthabens ein. Nach der fünften falschen Eingabe wird die Lösung angezeigt.
Das Guthaben beträgt €.
richtig: 0falsch: 0
Die Formel für die Ratenzahlung wird umgestellt, um das Anfangskapital zu berechnen.
| K0 = | Kn |
| (qn + qn-1 + qn-2 ··· + q1) |
Aufgabe 14: Oma Seeler legt bei der Geburt ihrer Enkelin 500 € auf ein Sparbuch. Anfang des zweiten und dritten Jahres zahlt sie jeweils noch 200 € ein. Das Sparbuch ist mit 3,5% verzinst. Welchen Betrag weist das Sparbuch am Ende des dritten Jahres auf?
Am Ende des dritten Jahres befinden sich ,60 € auf dem Sparbuch.
Versuche: 0
Aufgabe 15: Herr Kramer zahlte für seinen Ratensparvertrag jedes Jahr einen gleichgroßen Betrag ein. Das Geld wurde mit verzinst. Nach erhält er . Welche Rate hat er jedes Jahr eingezahlt? Runde auf ganze Euro.
Er zahlte jährlich € auf das Konto ein.
richtig: 0falsch: 0
Aufgabe 16: Franz möchte einen Ratenvertrag über drei Jahre aufsetzen. Der Zinssatz beträgt 2,7 %. Er hat vor, folgenden Beträge auf das Konto einzuzahlen:
1. Jahr: 500 €; 2. Jahr: 1000 €; 3. Jahr: 1500 €.
Später denkt er darüber nach, drei gleich bleibende Raten zu dem vorgesehenen Zinssatz einzuzahlen. Wie hoch läge die jährliche Rate, wenn Franz den gleichen Endbetrag erhalten wollte? Runde auf zwei Nachkommastellen.
Die gleich bleibenden Raten hätte eine Höhe von jeweils €.
Versuche: 0
Darlehen
Ein Darlehen ist ein großer Kredit bei einer Bank, der in gleichmäßigen Raten zurückgezahlt wird. Damit der Kredit getilgt werden kann, müssen die Rückzahlungs-Raten größer sein, als die jährlich anfallenden Zinsen.
Aufgabe 17: Klick bei den Beispielsdaten des Darlehens unterschiedliche Werte an und beobachte, wie sich Restschuld und Zinsen verändern.
Beispiel:
Darlehensbetrag:
€
Jährliche Verzinsung:
%
Jährliche Rückzahlungsrate:
€
| Jahr | Restschuld Jahresanfang |
+ Zinsen · |
- Rückzahlung Jahresende |
Restschuld Jahresende |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
Normalerweise findet eine Rückzahlung monatlich oder vierteljährlich statt.
Laufzeit beim Zinseszins
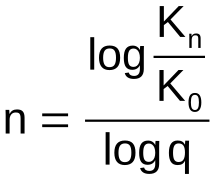
Aufgabe 18: Bei vertraglich festgelegten Zinssatz von 1,5 % wächst ein Kapital von anfänglich 100000 € auf 120000 € an. Wie lange war dieses Kapital angelegt? Runde auf ganze Jahre.
Der Vertrag hatte eine Laufzeit von Jahren.
richtig: 0falsch: 0

