Kathetensatz und Höhensatz
Kathetensatz
Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete genauso groß wie das Rechteck aus der Hypotenuse und dem anliegenden Hypotenusenabschnitt, der durch die Höhe markiert ist. Für die Grafik unten bedeutet das, die beiden blauen Flächen haben den gleichen Flächeninhalt und die beiden roten Flächen haben den gleichen Flächeninhalt.
b² = c · q
|
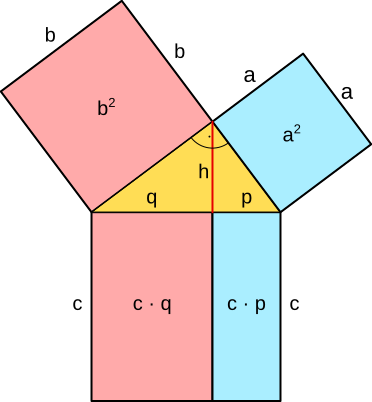 |
a² = c · p
|
Aufgabe 1: Ziehe die orangen Gleiter 1, 2, 3 in dieser Reihenfolge und versuche herauszufinden, weshalb a² und c · p die gleiche Größe aufweisen.
|
Aufgabe 2: Ziehe die orangen Gleiter. Du kannst erkennen, wie ein Rechteck mit Hilfe des Kathetensatzes zeichnerisch in ein Quadrat mit gleichem Flächeninhalt umgewandelt wird.
|
Aufgabe 3: Wandle im Heft wie im Beispiel von Aufgabe 2 ein Rechteck mit den Seitenlängen 9 cm und 4 cm zeichnerisch in ein Quadrat mit gleichem Flächeninhalt um.
Aufgabe 4: Gestalte im Heft ein Rechteck mit den Seitenlängen 10 cm und 2 cm. Wandle es zeichnerisch in ein Quadrat mit gleichem Flächeninhalt um. Berechne die Seitenlänge des Quadrates und vergleiche sie mit dem Wert deiner Zeichnung.
Aufgabe 5: Trage die Länge der mit x bezeichneten Strecke ein.

x = cm
Versuche: 0
Aufgabe 6: Trage die richtigen Werte in die Tabelle ein. Alle Aufgaben beziehen sich auf eine Dreieck mit der Hypotenuse c.
| a | b | c | p | q |
| 10 | 6,4 | |||
| 4,5 | 2,7 | |||
| 9 | 5,4 | |||
| 24 | 7 |
Werte in Meter (m)
Versuche: 0
Aufgabe 7: Die Hypotenuse (Seite c) eines rechtwinkligen Dreiecks setzt sich aus den Teilstrecken q = und p = zusammen. Berechne den Flächeninhalt der Quadrate über der Seite a und der Seite b.
| Das Quadrat über der Seite a hat einen Flächeninhalt von cm². |
| Das Quadrat über der Seite b hat einen Flächeninhalt von cm². |
richtig: 0falsch: 0
Höhensatz
Im rechtwinkligen Dreieck ist das Quadrat über der Höhe genauso groß wie das Rechteck aus den beiden Hypotenusenabschnitten p und q, die durch die Höhe unterteilt werden.
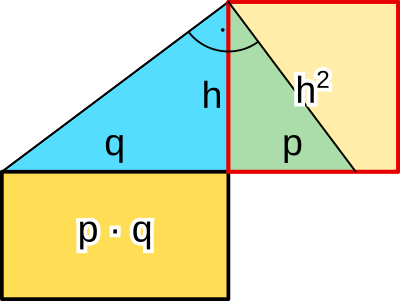 |
h² = p · q
|
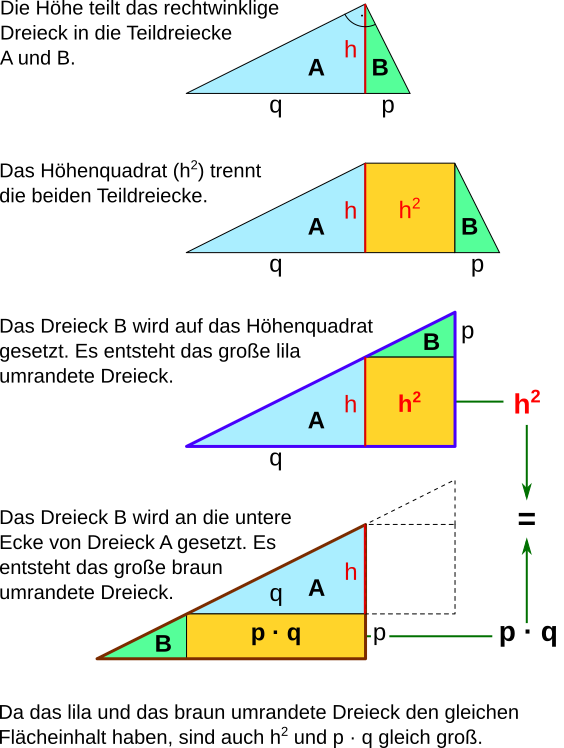
Aufgabe 8: Betrachte die folgende Grafik und versuche herauszufinden, weshalb in einem rechtwinkligen Dreieck h² genauso groß ist wie p · q.
Aufgabe 9: Trage die Länge der Strecke x unten ein.
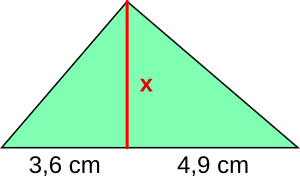
x = cm
Versuche: 0
Aufgabe 10: Ein rechtwinkliges Dreieck hat die angegebenen Hypotenusenabschnitte. Trage jeweils die Höhe ein.
| a) | p = 4 cm | q = 9 cm | h = cm |
| b) | p = 7 cm | q = 7 cm | h = cm |
| c) | p = 4,5 cm | q = 2 cm | h = cm |
Versuche: 0
Aufgabe 11: Ein rechtwinkliges Dreieck hat die Hypotenusenabschnitte p = 4,5 cm und q = 8 cm. Trage die Höhe (h) und die Seitenlängen (a, b) des Dreiecks ein.
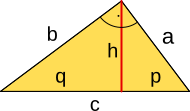
h = cm a = cm b = cm
Versuche: 0
Aufgabe 12: Die Höhe eines Dreiecks ist 6 cm, der Hypotenusenabschnitt p = 2,4 cm. Wie lang ist die Hypotenuse?
Die Hypotenuse hat eine Länge von cm.
Versuche: 0
Aufgabe 13: Wie groß sind bei dem abgebildeten Rechteck die Seiten a und b?
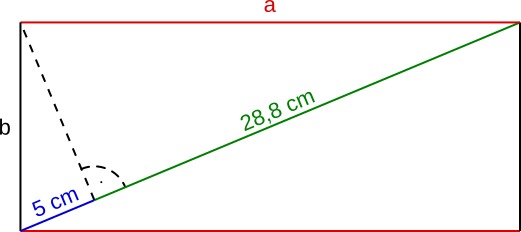
a = cm b = cm
Versuche: 0
Aufgabe 14: Ein Binnenschiff durchquert eine 13 Meter breite, halbkreisförmige Brücke. Die kistenförmige Ladung ist 5 Meter breit. Beim mittigen Durchfahren der Öffnung bleibt ein Abstand von 50 cm zur Brückendecke. Wie weit über dem Wasserspiegel befindet sich der obere Bereich der Ladung?
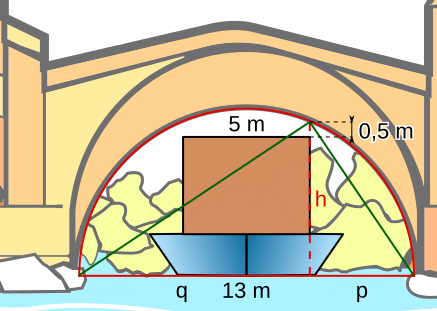
Die Ladung ragt bis in eine Höhe von m über dem Wasserspiegel.
Versuche: 0

