Strahlensätze
Werden zwei sich schneidende Strahlen von zwei parallelen Geraden durchkreuzt, so entstehen einander ähnliche Dreiecksfiguren, deren entsprechende Seiten im gleichen Verhältnis zueinander stehen.
Ähnliche Dreiecke
Zwei Dreiecke sind einander ähnlich, wenn
| • | sie in zwei gleichen Winkeln übereinstimmen. | ||||||||
| z. B. α = α' und γ = γ' |  |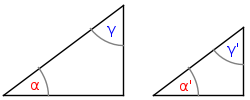
||||||||
| • | das Verhältnis zweier Seitenlängen gleich ist und der von beiden Seiten gebildete Winkel ebenfalls. |
||||||||
|
 |
||||||||
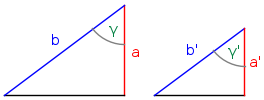| • | das Verhältnis zweier Seitenlängen gleich ist und der der längeren (kürzeren) Seite gegenüberliegende Winkel ebenfalls. |
||||||||
|
 |
||||||||
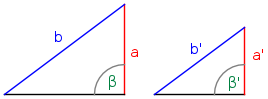Aufgabe 1: Bewege in der Grafik die orangen Gleiter. Die untenstehenden Terme zeigen das Verhältnis der angegebenen Seiten an. Klick unten jeweils den Term an, der in den roten Rahmen gehört.
|
= |
|
= |
|
= |
| a' |
| c' |
| b' |
| c' |
| a' |
| b' |
Versuche: 0
Aufgabe 2: Klick jeweils auf das rote Dreieck, dass dem blauen Dreieck ähnlich ist.
 |
 |
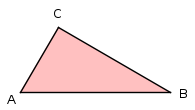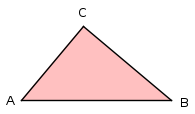richtig: 0 | falsch: 0
Aufgabe 3: Konstruiere mit Hilfe der Gleiter drei Dreiecke, die dem blauen Dreieck ähnlich sind.
richtig: 0 | falsch: 0
Aufgabe 4: Die beiden Dreiecke sind ähnlich zueinander. Trage die Länge der Seite a' ein.
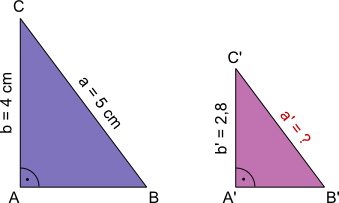
Antwort: Die Seite a' ist cm lang.
Versuche: 0
Aufgabe 5: Zu den Originaldreiecken A, B, C und D gibt es jeweils ein ähnliches Dreieck. Trage die fehlende Seitenlänge (b') des jeweils ähnlichen Dreiecks ein.
| Originaldreieck | A | B | C | D | |
| a | 6 cm | 5 cm | 8 cm | 8 cm | |
| b | 8 cm | 10 cm | 10 cm | 12 cm | |
| Ähnliches Dreieck | A' | B' | C' | D' | |
| a' | 3 cm | 7 cm | 12 cm | 18 cm | |
| b' | cm | cm | cm | cm | |
Versuche: 0
Aufgabe 6: Zu den Originaldreiecken A, B, C und D gibt es jeweils ein ähnliches Dreieck. Trage den richtigen Einer des fehlende Winkels (γ) beim jeweils ähnlichen Dreieck ein.
| Originaldreieck | A | B | C | D | |
| α | 90° | 90° | 90° | 90° | |
| β | 45° | 37° | 25° | 69° | |
| Ähnliches Dreieck | A' | B' | C' | D' | |
| α' | 90° | 90° | 90° | 90° | |
| γ | 4° | 5° | 6° | 2° | |
Versuche: 0
Aufgabe 7: Die vier Dreiecke A, B, C und D sind ähnlich zum abgebildeten Dreieck. Trage die fehlenden Seitenlängen der ähnlichen Dreiecke ein.
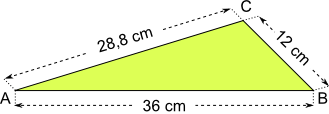
| Ähnliche Dreiecke | A | B | C | D |
| Seite a | 4 cm | cm | 2,5 cm | cm |
| Seite b | cm | cm | cm | 19,2 cm |
| Seite c | cm | 9 cm | cm | cm |
Versuche: 0
Strahlensätze
Wenn zwei sich schneidende Geraden von zwei Parallelen gekreuzt werden, entstehen gleichartige Seitenverhältnisse. Die Strahlensätze besagen, dass zwei Teilstrecken, die in die gleiche Richtung weisen, im gleichen Verhältnis zueinander stehen wie zwei weitere parallel zueinander stehende Teilstrecken, die in eine andere Richtung weisen.
Aufgabe 8: Bewege die orangen Gleiter und beobachte, in welchem Verhältnis die Seiten a1 a2 , b1 b2 und c1 c2 sowie die Seiten a1 a3 und b1 b3 zueinander stehen. Die entsprechenden Verhältnisse werden unten rechts angegeben.
1. Strahlensatz:
Das Verhältnis einander entsprechender Abschnitte auf den beiden Strahlen ist gleich:
| a1 | = | b1 | und | a1 | = | b1 |
| a2 | b2 | a3 | b3 |
2. Strahlensatz:
Der kurze Strahlenabschnitt verhält sich zum langen, wie der kurze Parallelenabschnitt zum langen:
| a1 | = | c1 | und | b1 | = | c1 |
| a2 | c2 | b2 | c2 |
Aufgabe 9: Klick auf das "Auto"-Button und beobachte, welche Streckenverhältnisse sich auf die jeweiligen Strahlensätze beziehen. Mit den Pfeil-Buttons kannst du von Grafik zu Grafik navigieren.
| © 2000 - http://geonext.de | |||||
 |
|||||
|
Aufgabe 10: Trage die Streckenbuchstaben so ein, das gültige Verhältnisse entstehen.
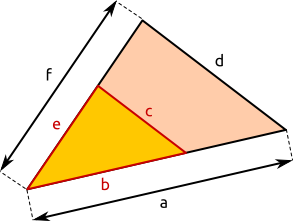
| a) | b | = | e | b) | b | = | c | c) | = | c | d) | b | = | a | e) | e | = | ||
| a | d | f | d | c | c | d |
Versuche: 0
Aufgabe 11: Trage jeweils die Länge von x ein.
| a) |  |
b) |  |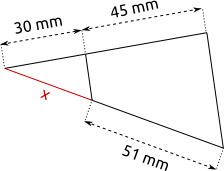
| x = mm | x = mm |
Versuche: 0
Aufgabe 12: Trage jeweils die Länge von x ein.
| a) |  |
b) |  |
| x = cm | x = mm |
Versuche: 0
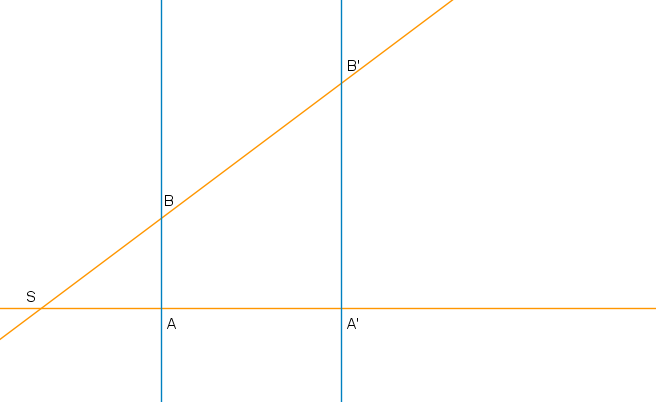
Aufgabe 13: Bewege die Gleiter und beobachte, was passiert.
Info: Die Strahlensätze gelten auch, wenn sich der Schnittpunkt (S) zwischen den parallelen Geraden befindet.
Aufgabe 14: Trage jeweils die Länge von x ein.
| a) |  |
b) |  |
| x = mm | x = mm |
Versuche: 0
Aufgabe 15: Trage jeweils die Länge von x ein.
| a) |  |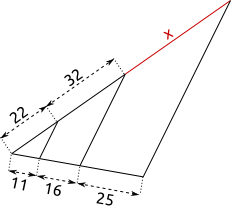
b) |  |
| Angaben in cm x = cm |
Angaben in cm x = cm |
Versuche: 0
Aufgabe 16: Trage jeweils die Länge von x ein.
| a) |  |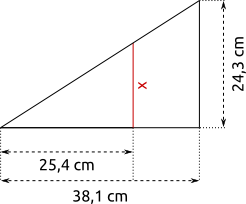
b) |  |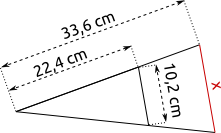
| x = cm | x = cm |
Versuche: 0
Aufgabe 17: Trage die Länge der Seite mit dem entsprechenden Buchstaben ein.
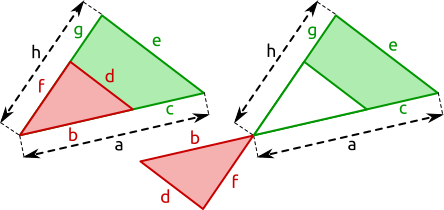
= cm
richtig: 0falsch: 0
Aufgabe 18: Trage jeweils die Länge von x und y ein.
| a) |  |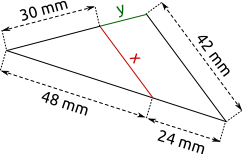
b) |  |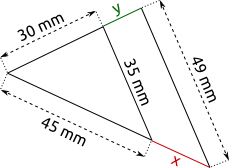
| x = mm; y = mm | x = mm; y = mm |
Versuche: 0
Aufgabe 19: Trage jeweils die Länge von x ein.
| a) |  |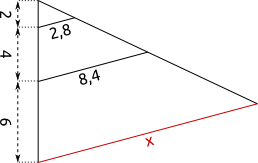
b) |  |
| Angaben in cm x = cm |
Angaben in cm x = cm |
Versuche: 0
Aufgabe 20: Trage die Länge von x und y ein. Beachte: Die Länge der unteren Dreiecksseite beträgt 3,6 cm + y cm.
x = cm; y = cm
Versuche: 0
Aufgabe 21: Trage die Länge der Seite mit dem entsprechenden Buchstaben ein.
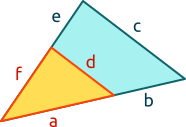
cm
richtig: 0falsch: 0
Aufgabe 22: Ein Förster misst mit einem gleichschenklig - rechtwinkligem Försterdreieck die Höhe der Bäume. Er hällt es waagerecht zum Boden und entfernt sich so weit vom Baum, bis er über die Längsseite des Dreiecks (Hypotenuse) die Baumspitze anpeilen kann. Wie hoch ist ein Baum, dessen Spitze der Förster aus 7,5 Meter Entfernung im Blick hat, wenn er das Dreieck in 1,6 Meter Höhe hält?
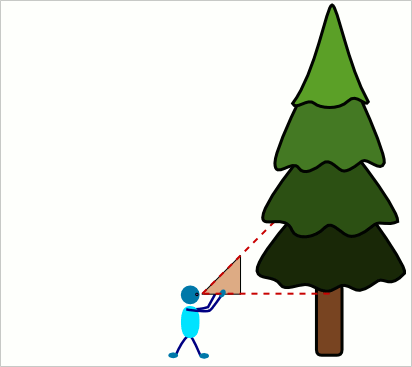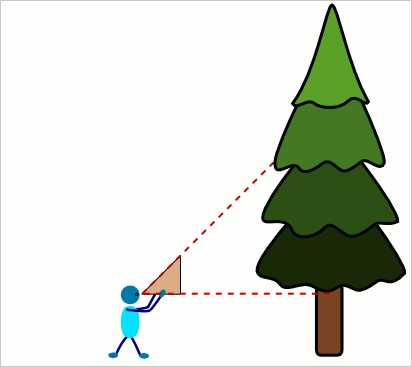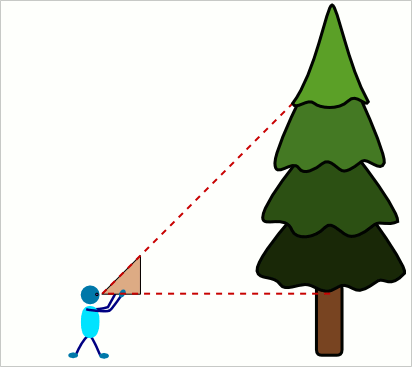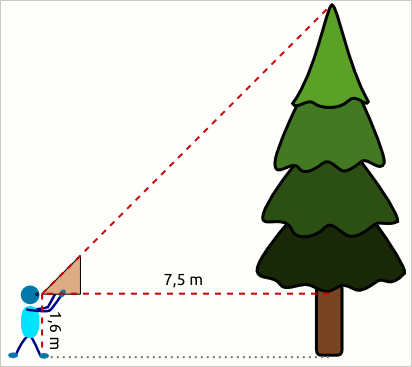
Antwort: Der Baum hat eine Höhe von m
Versuche: 0
Aufgabe 23: Unter einer Treppe soll ein 60 cm breiter Schrank eingebaut werden. Wie hoch kann der Schrank maximal sein? Runde auf Millimeter.
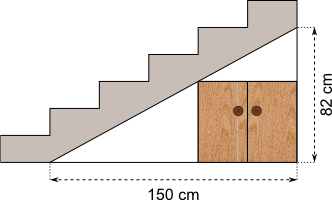
Antwort: Der Schrank kann maximal eine Höhe von cm haben.
Versuche: 0
Aufgabe 24: Die Länge eines unzugänglichen Sees wird vermessen. Die roten Strecken sind zueinander parallel. Trage den Wert unten ein.
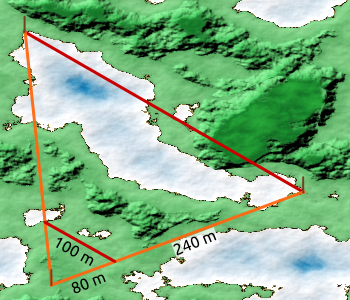
Antwort: Der See hat eine Länge von Metern.
Versuche: 0
Aufgabe 25: Auf der unteren Wegskizze ist die Strecke AD 240 m lang. Trage die Länge der Strecke BC ein.
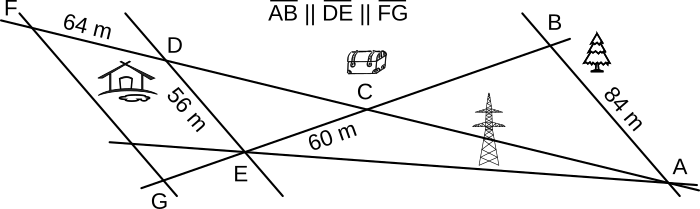
Länge BC: m
Versuche: 0
Aufgabe 26: Eine Pyramide hat eine Breite von 78 Metern. Wie breit ist sie auf der Hälfte (a) und nach dem ersten Drittel (b) ihrer Höhe?
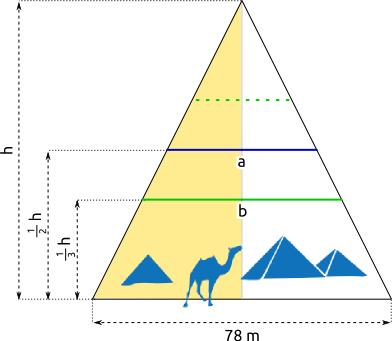
Antwort: Auf der Hälfte (a) ihrer Höhe hat die Pyramide eine Breite von Metern. Nach dem ersten Drittel (b) ihrer Höhe hat sie eine Breite von Metern.
Versuche: 0
Aufgabe 27: Die grüne Kegelform wird zweimal mit Gips ausgegossen. Der erste Gipskegel bleibt unversehrt. Der zweite Gipskegel wird auf halber Höhe so durchtrennt, dass ein Kegelstumpf übrig bleibt. Welches Volumen haben die beiden Körper? Runde auf ganze cm³.
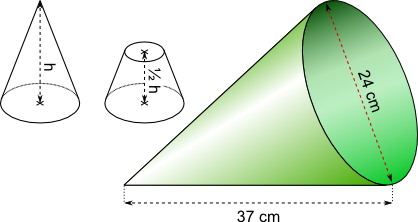
Antwort: Der Gipskegel hat ein Volumen von cm³ und der halb so hohe Kegelstumpf hat ein Volumen von cm³.
Versuche: 0
Aufgabe 28: Berechne die Länge der Strecke x.
Die Strecke x ist cm lang.
Versuche: 0
Aufgabe 29: In welchem Verhältnis stehen im unten abgebildeten regelmäßigen Sechseck die Seiten a und b zueinander? Kürze soweit wie möglich.
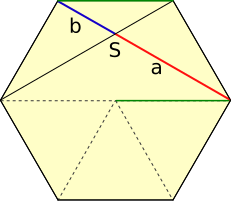
| Das Verhältnis der Seiten | a | ist gleich | . | |
| b |
Versuche: 0
Aufgabe 30: Über einen Fluss soll eine neue Brücke gebaut werden. Wie lang muss die Brücke (x) werden?
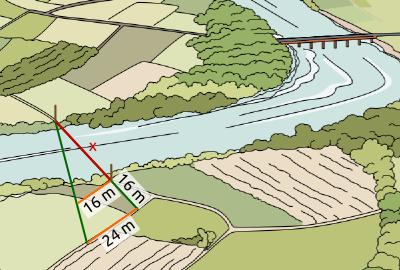
Antwort: Die Brücke muss eine Strecke von Metern überwinden.
Versuche: 0