Logarithmus
Wenn von einer Potenz nicht der Potenzwert, sondern die Basis gesucht wird, dann erlangt man das Ergebnis über das Wurzelziehen. Der Logarithmus gibt an, mit welchem Exponenten man eine Basis potenzieren muss um einen bestimmten Wert zu erreichen.
| Aufgabe | gesucht | Rechnung | Ergebnis | |
| a) | 23 = a | Potenzwert | 23 = 8 | Potenzwert |
| b) | b3 = 8 | Basis | Wurzel | |
| c) | 2x = 8 | Exponent | log2 8 = 3 | Logarithmus |
| Allgemein: | ||||
| bx = a | logb a = x | |||
| (a, b > 0 und b ≠ 1) | ||||
Sprich: x ist Logarithmus von a zur Basis b
Begriffe: 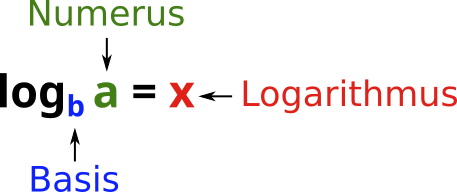
Beispiel:
| log2 8 = 3 | ; denn 23 = 8 | ||||||||||
| log10 100 = 2 | ; denn 102 = 100 | ||||||||||
| log3 81 = 4 | ; denn 34 = 81 | ||||||||||
|
|
||||||||||
| log6 1 = 0 | ; denn 60 = 1 | ||||||||||
| ; denn |
|||||||||||
Aufgabe 1: Trage Basis, Numerus und Logarithmus richtig ein.
a) → log = b) → log =
richtig: 0falsch: 0
Aufgabe 2: Trage den Logarithmus ein.
a) = b) =
richtig: 0falsch: 0
Aufgabe 3: Trage den Logarithmus ein.
| a) | = | b) | = |
richtig: 0falsch: 0
Aufgabe 4: Ergänze den Logarithmus.
| a) log4 2 = | 1 | b) log27 3 = | 1 | c) log16 2 = | 1 |
Versuche: 0
Aufgabe 5: Ergänze den Logarithmus.
| a) | log2 2√2 = |
|
b) | log3 2√3 = |
|
||||
| c) | log2 3√2 = |
|
d) | log3 3√3 = |
|
||||
| e) | loga 2√a = |
|
f) | logb 3√b = |
|
||||
richtig: 0falsch: 0
Aufgabe 6: Trage den Numerus ein.
a) log b) log
richtig: 0falsch: 0
Aufgabe 7: Trage den Numerus ein.
|
Versuche: 0
Aufgabe 8: Ergänze den Numerus.
|
richtig: 0falsch: 0
Aufgabe 9: Trage die Basis ein.
a) log b) log
richtig: 0falsch: 0
Aufgabe 10: Trage die Basis ein.
| a) log 5 = 1 | b) log 2 = 1 |
| c) log 7 = 1 | d) log 8 = 1 |
richtig: 0falsch: 0
Aufgabe 11: Trage die Basis ein.
|
richtig: 0falsch: 0
Aufgabe 12: Trage die Basis ein.
|
richtig: 0falsch: 0
Aufgabe 13: Ergänze die Basis.
| a) log | 1 | 64 = -2 | b) log | 1 | 49 = -2 |
| c) log | 1 | 27 = -3 | d) log | 1 | 16 = -4 |
Versuche: 0
Aufgabe 14: Ergänze die Basis.
| a) log2 ( ) = | b) log3 ( ) = |
| c) log ( +-) = 2 | d) log10 ( +-) = 3-6 |
richtig: 0falsch: 0
Basiswechsel
Dividiert man den Zähler eines Bruches durch den Teiler 1, bleibt sein Wert erhalten. Dieser Wert verändert sich ebenfalls nicht, wenn Zähler und Teiler proportional vergrößert oder verkleinert werden. Im Beispiel wird der Logarithmus von 256 zur Basis 16 geteilt durch den Logarithmus von 16 zur Basis 16 - also durch 1. Der Wert des Bruchs ist genauso groß wie der Wert des Logarithmus. Gibt man dem Logarithmus im Zähler und im Nenner eine andere Basis (z.B. 4, 2, 10...) dann verändern sich Zähler und Nenner proportional. Das Ergebnis des Bruches bleibt somit gleich. Diesen Umstand nutzt man, um mit dem Taschenrechner den Logarithmus auszurechnen.
| log16 256 = 2 | → | log16 16 = 1 | → |
|
|||||
| log4 256 = 4 | → | log4 16 = 2 | → |
|
|||||
| log2 256 = 8 | → | log2 16 = 4 | → |
|
|||||
| log10 256 = 2,4... | → | log10 16 = 1,2... | → |
|
|||||
|
|||||||||
Da der Taschenrechner keinen Logarithmus zur Basis 16 angibt, kann man sich mit dem Logarithmus zur Basis 10 aushelfen, indem der Logarithmus von 256 zur Basis 10 durch den Logarithmus von 16 zur Basis 10 geteilt wird. Grundsätzlich kann also der Logarithmus von x zur Basis a bestimmt werden, indem der Logarithmus von x zur Basis 10 durch den Logarithmus von a zur Basis 10 geteilt wird.
| loga (x) = | lg (x) |
| lg (a) |
lg = Logarithmus zur Basis 10
Aufgabe 15: Berechne den Logarithmus auf drei Nachkommastellen gerundet.
log =
richtig: 0falsch: 0
Aufgabe 16: Berechne den Logarithmus auf drei Nachkommastellen gerundet.
log =
richtig: 0falsch: 0
Aufgabe 17: Berechne den Logarithmus auf drei Nachkommastellen gerundet.
log √ =
richtig: 0falsch: 0
Aufgabe 18: Berechne das Ergebnis auf drei Nachkommastellen gerundet.
| log | = | |
richtig: 0falsch: 0
Aufgabe 19: Berechne das Ergebnis auf drei Nachkommastellen gerundet.
(log )2 + log =
richtig: 0falsch: 0
Aufgabe 20: Berechne das Ergebnis auf drei Nachkommastellen gerundet.
· log =
richtig: 0falsch: 0
Aufgabe 21: Berechne das Ergebnis auf drei Nachkommastellen gerundet.
| = | |
| log |
richtig: 0falsch: 0
Logarithmengesetze
für u>0, v>0, x>0, a>0, a ≠ 1
- Ein Produkt wird logarithmiert, indem man die einzelnen Faktoren logarithmiert und die Ergebnisse addiert.
loga (u · v) = loga (u) + loga (v) - Ein Bruch wird logarithmiert, indem man die einzelnen Faktoren logarithmiert und die Ergebnisse subtrahiert.
loga 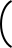
u 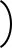 = loga (u) - loga (v)
= loga (u) - loga (v)v - Eine Potenz wird logarithmiert, indem man die Basis logarithmiert und das Ergebnis mit dem Exponenten multipliziert.
loga (ut) = t · loga (u)
Aufgabe 22: Ordne die richtigen Terme zu.
| a) loga (x · y) = | b) loga
|
| c) loga
|
d) loga (v · w) = |
loga v + loga w loga v - loga w loga x + loga y loga x - loga y
Versuche: 0
Aufgabe 23: Ordne die richtigen Terme zu.
| a) loga (x · y · z) = |
| b) loga
|
| c) loga
|
| d) loga (x · (y + z)) = |
loga x + loga y - loga z loga x + loga y + loga z loga x + loga (y + z) loga x - loga y - loga z
Versuche: 0
Aufgabe 24: Ordne die richtigen Terme zu.
| a) loga ((v + w) · (x - y)) = |
| b) loga
|
| c) loga
|
|
d) loga
|
loga (v + w) - loga (x - y) loga (v + w) + loga (x - y) loga v + loga w + loga x - loga y loga v + loga w - loga x - loga y
Versuche: 0
Aufgabe 25: Ordne die richtigen Terme zu.
| a) loga
|
| b) loga
|
| c) loga
|
- loga x - loga y - loga z - loga (r + s) loga x + loga y - loga z - loga (r + s) loga x + loga (r + s) - loga y - loga z
Versuche: 0
Aufgabe 26: Ordne die richtigen Terme zu.
| a) loga |
b) loga |
| c) loga
|
d) loga |
| e) loga
|
f) loga
|
1 2 loga x 1 4 loga x -2 loga x -4 loga x 2 loga x 4 loga x
Versuche: 0
Aufgabe 27: Ordne die richtigen Terme zu.
| a) loga (x · y)2 = |
| b) loga
|
| c) loga |
| d) loga
|
| e) loga
|
| f) loga
|
2 loga x + 4 loga y 2 loga x + 2 loga y loga x + 2 loga y 2 loga x - 2 loga y 2 loga x - 4 loga y -2 loga x - 4 loga y
Versuche: 0
Aufgabe 28: Ordne die richtigen Terme zu.
| a) loga |
| b) loga |
| c) loga |
| d) loga |
| e) loga
|
| f) loga
|
½ loga x - ½ loga y ½ loga x + ½ loga y loga x + 2 loga y loga x + ½ loga (y + z) loga x - 2 loga (y + z) loga x + 2 loga (y - z)
Versuche: 0
Aufgabe 29: Ordne die richtigen Terme zu.
| a) loga x + loga y - loga z = |
| b) 3 loga x + 5 loga y - 2 loga z = |
| c) 3 loga x - (loga y + ½ loga z) = |
| d) 2 loga (x - y) - 1 3 loga (x+y) = |
| e) 1 3 loga (x2 + y2) - 2 loga x = |
loga ![]()
![]()
![]() loga
loga
![]()
![]()
![]() loga
loga
![]() x3y5
z2
x3y5
z2
![]() loga
loga
![]()
![]()
![]() loga
loga
![]() xy
z
xy
z
![]()
Versuche: 0
Aufgabe 30: Ordne die richtigen Terme zu.
| a) log3 6 - log3 2 + log3 1 = = = |
| b) log2 4 + log2 12 - log2 3 = = = |
| c) log5 6x + log5 1 3x + log5 12,5 = = = |
| d) loga (x + 1) + loga (x - 1) - loga (x² - 1) = = = |
| e) log3 27x x = = = |
log2
![]() 4 · 12
3
4 · 12
3
![]() log3
log3
![]() 6 · 1
2
6 · 1
2
![]()
![]() x · log3 27
x
x · log3 27
x
![]() log5
log5 ![]() 6x
3x
· 12,5
6x
3x
· 12,5![]() loga
loga ![]() (x + 1)(x - 1)
x² - 1
(x + 1)(x - 1)
x² - 1
![]() loga 1
log3 3
log2 16
log5 25
log3 27
0
1
2
3
4
loga 1
log3 3
log2 16
log5 25
log3 27
0
1
2
3
4
Versuche: 0
Exponentialgleichung
Steht die Variable im Exponenten, dann handelt es sich um eine Exponentialgleichung. Gelöst werden Exponentialgleichungen nach folgendem Schema:
Beispiel: 23x - 5 + 6 = 134 | ||||||
| • | Variable isolieren | 23x - 5 = 128 | ||||
| • | Logarithmieren | lg (23x - 5) = lg 128 | ||||
| • | Logarithmengesetze anwenden | (3x - 5) · lg 2 = lg 128 | | : lg 2 | |||
| • | Nach Variable auflösen |
| | + 5 | : 3 | |||
| ||||||
Aufgabe 31: Bestimme x auf drei Nachkommastellen gerundet.
x =
x =
richtig: 0falsch: 0
Aufgabe 32: Bestimme x auf drei Nachkommastellen gerundet.
(x) =
| Hilfe | ||||
| lg (a x n) | = | lg b | ||
| (x n) · lg a | = | lg b | ||
| x · lg a n · lg a | = | lg b | ||
| x · lg a | = | lg b n · lg a | ||
| x | = |
|
||
x =
richtig: 0falsch: 0
Aufgabe 33: Bestimme x auf drei Nachkommastellen gerundet.
![]() =
=
| Hilfe | ||||
| lg (a |
= | |||
| lg (a |
= | lg b | ||
| = | lg b | |||
| lg a | = | lg b · x | ||
|
= | x | ||
x =
richtig: 0falsch: 0
Aufgabe 34: Bestimme x auf drei Nachkommastellen gerundet.
a · bcx = dxe
| Hilfe | ||||
| lg (a · bnx) | = | lg (cx - m) | ||
| lg a + nx · lg b | = | (x - m) · lg c | ||
| lg a + nx · lg b | = | x · lg c - m · lg c | ||
| lg a - m · lg c | = | x · lg c - nx · lg b | ||
| lg a - m · lg c | = | x · (lg c - n · lg b) | ||
|
= | x | ||
x =
richtig: 0falsch: 0
Aufgabe 35: Bestimme x auf drei Nachkommastellen gerundet.
a · bx + 1 = cx - 1
| Hilfe | ||||
| lg (a · bx + 1) | = | lg (cx - 1) | ||
| lg a + (x + 1) · lg b | = | (x - 1) · lg c | ||
| lg a + x · lg b + lg b | = | x · lg c - lg c | ||
| lg a + lg b + lg c | = | x · lg c - x · lg b | ||
| lg a + lg b + lg c | = | x · (lg c - lg b) | ||
|
= | x | ||
x =
richtig: 0falsch: 0
Aufgabe 36: Bestimme x auf drei Nachkommastellen gerundet.
f · dxe = a · bcx
| Hilfe | ||||
| lg (a · bx - n) | = | lg (c · dmx) | ||
| lg a + (x - n) · lg b | = | lg c + mx · lg d | ||
| lg a + x · lg b - n · lg b | = | lg c + mx · lg d | ||
| x · lg b - mx · lg d | = | lg c - n · lg b - lg a | ||
| x · (lg b - m · lg d) | = | lg c - n · lg b - lg a | ||
| x | = |
|
||
x =
richtig: 0falsch: 0
Aufgabe 37: Herr Pecunia legt zu einem Zinssatz von an. Nach welcher Zeit verbucht er (Zinsen und Zinseszinsen eingerechnet) auf seinem Konto? Runde auf eine Stelle nach dem Komma.
Herr Pecunia verbucht nach Jahren auf seinem Konto.
richtig: 0falsch: 0

