Terme mit Variablen aufstellen
- Terme sind Rechenausdrücke.
(3 + 2; 4 · 5; 24 : 6; 12 - 3; ...) - Terme mit Variablen (Platzhaltern) sind Rechenausdrücke mit
kleinen Buchstaben, die veränderbare Größen kennzeichnen.
(2 · x; 5a + 7; p · q) - Gleichartige Terme sind Rechenausdrücke mit
gleichen Variablen.
(x; 4 · x; 3,2x -1,4; ... ) - Gleichungen entsteht durch das Verbinden von zwei Termen mit einem Gleichheitszeichen.
(2x + 2 = 17 - x; ...)
- Der Wert eines Terms ist erst bestimmbar, wenn jeder Variable eine Zahl zugeordnet ist.
Aufgabe 1: Stelle unten mit den orangen Gleitern unterschiedliche Terme für die dargestellte Strecke ein. Probiere aus, wie sich die Strecke verändern kann.
Aufgabe 2: Trage die Streckenlängen zu folgenden Streckentermen ein. Du kannst die Aufgaben auch mit der Grafik in Aufgabe 1 nachstellen.
| Strecken- term |
x = | y = | Strecken- länge |
Strecken- term |
x = | y = | Strecken- länge |
|
| 1x + 5y | 2 cm | 3 cm | cm | 4x + 2y | 5 cm | 4 cm | cm | |
| 2x + 4y | 4 cm | 5 cm | cm | 5x + 1y | 3 cm | 2 cm | cm | |
| 3x + 3y | 2 cm | 4 cm | cm | 0x + 6y | 5 cm | 2 cm | cm |
Versuche: 0
Aufgabe 3: Trage den Umfang der Figuren ein.
a) 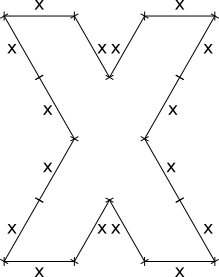 |
b) 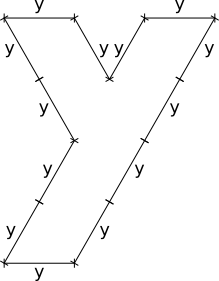 |
| x = 4 cm Figur a hat einen Umfang von cm. |
y = 5 cm Figur b hat einen Umfang von cm. |
Versuche: 0
Aufgabe 4: Ordne die jeweilige Figur dem Term zu, der den entsprechenden Umfang der Figur angibt. Alle kurzen Seiten haben die Länge x und alle langen Seiten die Länge y.
Aufgabe 5: Trage unten den Umfang der oberen Figuren ein, wenn x 5 mm und y 8 mm lang ist?.
|
Alle Figuren mit dem Umfang 12x + 2y haben dann einen Umfang von mm. Alle Figuren mit dem Umfang 10x + 3y haben dann einen Umfang von mm. Alle Figuren mit dem Umfang 8x + 4y haben dann einen Umfang von mm. |
Versuche: 0
Aufgabe 6: Auf das folgende Armband sind unterschiedliche Perlen aufgefädelt.
a) Ergänze den vereinfachten Term für die Armbandlänge.
b) Trage die Länge des Armbandes ein.
Perle a ![]() 15 mm | Perle b
15 mm | Perle b ![]() 12 mm | Perle c
12 mm | Perle c ![]() 6 mm
6 mm
![]()
a) Vereinfachter Term der Länge: a + b + c b) Das Armband ist cm lang. |
Versuche: 0
Aufgabe 7: Klick den Term an, der den Umfang der geometrischen Figur wiedergibt.
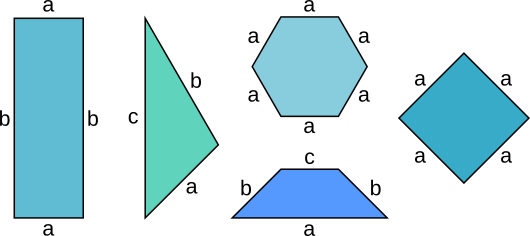
| Dreieck
|
Quadrat
|
| Rechteck
|
Trapez
|
| Sechseck
|
Versuche: 0
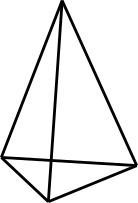
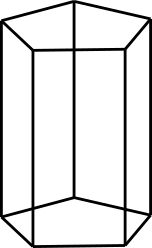
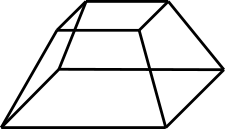
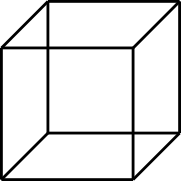
Aufgabe 8: Die folgenden Körper bestehen aus Draht. Klick darunter die Terme an, die zu den Kanten des jeweiligen Körpers passen.
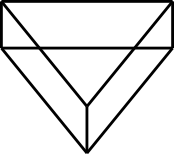 |
 |
 |
 |
 |
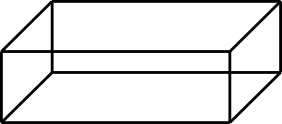 |
Versuche: 0
Aufgabe 9: Trage in die Tabelle die richtigen Ergebnisse ein.
| x | x · | x · |
| 0 | ||
| 1 | ||
| 2 | ||
| 1,5 | ||
| 2½ |
Versuche: 0
Aufgabe 10: Trage den für die Variable gewählten Wert ein.
| x | x + |
| 52 | |
| 73 | |
| 26,5 | |
| 64,2 |
Versuche: 0
Aufgabe 11: Vervollständige die Tabelle
| x | x+ | x | x - | x : |
richtig: 0falsch: 0
Aufgabe 12: Klick den richtigen Term für jede Wertetabelle an.
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
Versuche: 0
Aufgabe 13: Ordne die richtigen Terme einander zu.
|
a) 7x – 3x = b) 5x + 6x = c) 3x + 2x + 5x = d) 8x + 6x – 2x = e) x + y + y + y= f) x + x + y + y – y = Versuche: 0 |
Aufgabe 14: Ordne jedem Satz einen Term zu.
| a) | Durch den Umzug hat sich Heikos Schulweg verdoppelt. | |
| b) | Drei Leute teilen sich eine Pizza. | |
| c) | Sabine erhält diesen Monat nur die Hälfte ihres Taschengeldes. | |
| d) | Brunos Vertrag wurde um 3 Jahre verlängert. | |
| e) | Bei Regen kommt nur ein Viertel der sonst üblichen Besucher in den Park. | |
| f) | Mit einem Flaschenzug kann man das dreifache Gewicht heben. | |
| g) | Das Schlauchboot kostet jetzt 20 € weniger als die Hälfte seines alten Preises. | |
| h) | Wenn ihr die doppelte Menge Bälle kauft, erhaltet ihr noch 5 weitere kostenlos dazu. |
Versuche: 0
Aufgabe 15: Klick auf die Rechenzeichen, die zum roten Begriff passen.
Wort
richtig: 0 | falsch: 0
Aufgabe 16: Füge in der zweiten Spalte den zum Text gehörigen Term zusammen und berechne ihn mit x = . Trage das Ergebnis in die letzte Spalte ein.
| Text | Term | Ergebnis (x = ) |
|
| Vermehre das Zweifache einer Zahl um 5. | = | ||
| Vermindere das Fünffache einer Zahl um 2. | = | ||
| Vermehre das Doppelte einer Zahl um das Fünffache einer Zahl. | = | ||
| Bilde das Produkt aus dem Doppelten einer Zahl und 5 | = | ||
| Halbiere eine Zahl und füge 2,5 hinzu. | = | ||
| Subtrahiere eine Zahl von 8. | = | ||
| Dividiere eine Zahl durch 0,5. | = | ||
| Vermindere das Zweifache einer Zahl um 5. | = |
Versuche: 0

Hier klicken
Aufgabe 17 a: Ein LED-Display ist in 7 Leuchtstreifen (s) eingeteilt. (Hier klicken.) Erstelle unten einen Term für die Anzahl der aufleuchtenden Streifen bei folgenden Ziffern:
| 1 | 2 | 3 | |||
 |
 |
 |
|||
| s | + | s | + | s | = s |
richtig: 0 | falsch: 0
Aufgabe 17 b: Bei welcher dreistelligen Zahl leuchten im oberen Display die wenigsten Leuchtstreifen?
Die wenigsten Streifen leuchten bei der Zahl .
Versuche: 0
Aufgabe 17 c: Bei welcher dreistelligen Zahl leuchten im oberen Display die meisten Leuchtstreifen?
Die meisten Streifen leuchten bei der Zahl .
Versuche: 0
Aufgabe 18: Vervollständige die Terme für den Umfang und die Fläche der folgenden Figur.

u = · a + · 3 + · 5 u = (a + ) · + 5 · |
A = (a + ) · A = a · + 3 · |
Versuche: 0
 Aufgabe 19 a: Max will sich aus einer Messingplatte die rechte "digitale" Hausnummer aus gleichgroßen
Schlitzen der Länge a und der Breite b fräsen. Er lässt einen Rand in Schlitzbreite b.
Aufgabe 19 a: Max will sich aus einer Messingplatte die rechte "digitale" Hausnummer aus gleichgroßen
Schlitzen der Länge a und der Breite b fräsen. Er lässt einen Rand in Schlitzbreite b.
Trage unten die richtigen Zahlen in die Terme ein, die die Höhe und die Breite der Messingplatte bestimmen.
| a: (Term für die Höhe) a + b b: (Term für die Breite) a + b |
Versuche: 0
Aufgabe 19 b: Die Schlitze von Max' Hausnummer sollen 80 mm lang und 20 mm breit sein. Wie hoch und wie breit muss dann die Messingplatte für die Hausnummer 5 sein? (a = 80 mm; b = 20 mm)
Die Messingplatte hat eine Höhe von cm und eine Breite von cm
Versuche: 0
Aufgabe 19 c: Vervollständige den Term für die Deckfläche der Hausnummer.
ADeckfläche = (a + b) · (a + b) - (a · b)
Versuche: 0
Aufgabe 20: Vervollständige die Terme für das Volumen des Gesamtquaders.
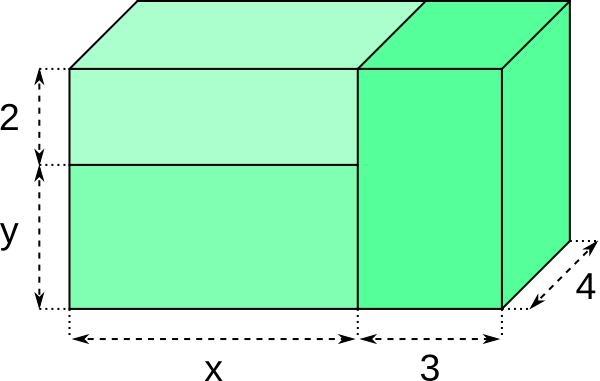
V = (2 + ) · ( + x) ·
Versuche: 0
Aufgabe 21: Vervollständige die Terme für den Flächeninhalt der folgenden Figur.

|
Versuche: 0

