Monats- und Tageszins
- Zinsen einfacher Zeiträume (A 2 - A 5)
- Rechnung mit zwei Dreisätzen (A 6 - A 8)
- Zinsformeln (A 9 - A 10)
- Zinsen (A 11 - A 12)
- Zinssatz (A 13 - A 14)
- Kapital (A 15 - A 16)
- Zeit (A 17 - A 18)
- Gemischte Aufgaben (A 19 - A 33)
- Ratenkredit (A 34 - A 35)
Aufgabe 1: Trage die richtigen Werte ein.
- Zinsen werden prinzipiell für ein (rahJ) berechnet. Kleiner Zeiträume berechnen Geldinstitute mit folgende Werte:
- Ein Jahr wird grundsätzlich in Tage, Wochen oder Monate eingeteilt.
- Ein Monat wird generell in Tage eingeteilt.
Versuche: 0
Aufgabe 2: In 12 Monaten erhältst du Zinsen. Trage die Zinsen ein, die du in den angegebenen Zeiträumen erhältst.
| Zeitraum | Zinsen | ||
| 12 Monate | € | ||
| : 2 |
: 2 | ||
| 6 Monate | € | ||
| 3 Monate | € | ||
| 4 Monate | € | ||
richtig: 0falsch: 0
Aufgabe 3: In 180 Tagen erhältst du Zinsen. Trage die Zinsen ein, die du in den angegebenen Zeiträumen erhältst.
| Zeitraum | Zinsen | ||
| 360 Tage | € | ||
| · 2 |
· 2 | ||
| 180 Tage | € | ||
| 90 Tage | € | ||
| 20 Tage | € | ||
richtig: 0falsch: 0
Aufgabe 4: Frau Moos legt Kapital von zu an. Klick die richtigen Rechnungen an und trage die Zinsen für die angegebenen Zeiträume ein.
| Zinsen im |
|
Zinsen im |
||
| |
 |
: = € | Halbjahr | |
| = € | Jahr | : = € | Vierteljahr | |
| : = € | Monat | |||
richtig: 0falsch: 0
Aufgabe 5: Trage unten die jeweiligen Jahreszinsen und die Zinsen der angegebenen Tage ein.
| Kapital | Zins- satz |
Jahres- zinsen |
Zeit in Tagen |
Zinsen | |
| a) | € | 180 | € | ||
| b) | € | 90 | € | ||
| c) | € | 36 | € |
richtig: 0falsch: 0
Zinsen werden normalerweise für ein Jahr ausgewiesen (Jahreszinsen). Bei anderen Zeiträumen (Tage, Monate, Jahre) lassen sich die jeweiligen Größen mit dem Dreisatz oder durch Zinsformeln berechnen.
Dreisatz
Aufgabe 6: Für die Berechnung der Zinsgrößen mithilfe des Dreisatzes benötigt man zwei Rechenschritte. Im ersten Schritt werden stets die Jahreszinsen gesucht. Im zweiten Schritt wird die gesuchte Größe ermittelt.
- Klick auf das Klappmenü neben "gesucht" und markiere eine der angegebenene Größen.
- Verschiebe die orangen Gleiter und den Monatsregler.
- Schritt 1: Überlege, wie du die Jahreszinsen berechnen kannst.
- Schritt 2: Überlege, wie du die gesuchte Größe mit Hilfe der Jahreszinsen berechnen kannst.
Grüne Skala: Verhältnis Kapital (K), Zinssatz (p%), Jahreszinsen (ZJ)
Blaue Skala: Verhältnis Jahreszinsen, Monatsrate (ZM)
gesucht:
Aufgabe 7: Stelle in Aufgabe 6 die Daten in den einzelnen Tabellenzeilen ein. Lies die gesuchten Werte ab und trage sie ein.
| Kapital (K) | Zinssatz (p%) | Zeit (M) | Zinsen (Z) | |
| a) | 1600 € | 4 % | 3 Monate | € |
| b) | 1600 € | 5 % | 3 Monate | € |
| c) | 1800 € | % | 1/2 Jahr | 27 € |
| d) | 2200 € | 4 % | Monate | 66 € |
| e) | € | 8 % | 10 Monate | 160 € |
Versuche: 0
Info: Für Geldinstitute gilt, dass ein Jahr 360 und ein Monat 30 Tage hat.
Aufgabe 8: Klick jeweils die richtigen Werte an.
|
a) Zinsen mit Dreisatz ermitteln geg: K = 2000 €, p = 6%, M = 3 Monate ges: Z Schritt 1: Jahreszinsen berechnen
Schritt 2: Zeitraumzinsen berechnen
Versuche: 0 |
b) Kapital mit Dreisatz ermitteln geg: Z = 30 €, p = 6%, M = 3 Monate ges: K Schritt 1: Jahreszinsen berechnen
Schritt 2: Kapital berechnen
Versuche: 0 |
||||||||||||||||||||||||||||||||||||||||||
| c) Zinssatz mit Dreisatz ermitteln geg: K = 2000 €, Z = 30 €, M = 3 Monate ges: p Schritt 1: Jahreszinsen berechnen
Schritt 2: Zinssatz berechnen
Versuche: 0 |
d) Zeit mit Dreisatz ermitteln geg: K = 2000 €, p = 6%, Z = 30 € ges: M Schritt 1: Jahreszinsen berechnen
Schritt 2: Zeit berechnen
Versuche: 0 |
Im folgenden Schema sind die oberen Rechenschritte nochmals zusammengefasst.
| gesucht | Schritt 1 berechne die Jahreszinsen (ZJ) |
Schritt 2 berechne die gesuchte Größe |
||||||
| a) Zinsen (Z) | ZJ | = | K : 100 · p | Z = | ZJ | : 12 · Monate | ||
| b) Kapital (K) | Z : M · 12 | K = | ZJ | : p · 100 | ||||
| c) Zinssatz (p%) | Z : M · 12 | p% = 100% : K · | ZJ | |||||
| d) Zeit (M) | K : 100 · p | M = 12 : | ZJ | · Z | ||||
Zur Vereinfachung wird die Zeit hier in Monaten angegeben. |
||||||||
Zinsformeln
Zinsen lassen sich mit Hilfe von 4 Formeln berechnen, die folgendes Muster aufweisen.
- Werden die Zinsen gesucht, steht im Nenner der Formel 360 · 100.
Alle übrigen Größen werden im Zähler miteinander multipliziert.
- Werden die Zinsen nicht gesucht, steht im Zähler der Formel Z · 360 · 100.
Alle übrigen Größen, außer der gesuchten Größe, werden im Nenner miteinander multipliziert.
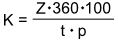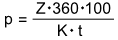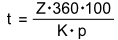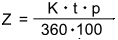
Aufgabe 9: Klick die Terme so an, dass die richtigen Formeln entstehen..
K = Kapital | p = Zinssatz | t = Verzinsungszeit | Z = Zinsen
| K = |
p = | Zähler | ||||
| Nenner | ||||||
| t = | Z = | |||||
Versuche: 0
Aufgabe 10: Ordne zu, bei welchen Größen die angegebenen Terme im Zähler, beziehungsweise im Nenner stehen.
Aufgabe 11: Trage die fehlenden Zinsen ein. Rechne zuerst den Jahreszins aus. Nach dem fünften falschen Eintrag wird die Lösung angezeigt.
| Kapital | Zinssatz | Zinsen für Zeitraum | |
| € | Monate | ||
| € | Tage | ||
richtig: 0falsch: 0
Aufgabe 12: Manuel hat Monate lang € auf seinem Sparbuch. Wie hoch sind die Zinsen bei einem Zinssatz von %?
Manuel erhält € Zinsen.
richtig: 0falsch: 0
Aufgabe 13: Trage den fehlenden Zinssatz ein. Rechne zuerst den Jahreszins aus. Nach dem fünften falschen Eintrag wird die Lösung angezeigt.
| Kapital | Zinssatz | Zinsen für Zeitraum | |
| % | Monate | ||
| % | Tage | ||
richtig: 0falsch: 0
Aufgabe 14: Frauke erhält nach Monaten für € Sparguthaben € Zinsen. Wie hoch ist der Zinssatz?
Der Zinssatz beträgt %.
richtig: 0falsch: 0
Aufgabe 15: Trage das fehlenden Kapital ein. Rechne zuerst den Jahreszins aus. Nach dem fünften falschen Eintrag wird die Lösung angezeigt.
| Kapital | Zinssatz | Zinsen für Zeitraum | |
| € | Monate | ||
| € | Tage | ||
richtig: 0falsch: 0
Aufgabe 16: Herr Mertens nimmt einen Kredit mit einer Laufzeit von Monaten auf. Die Bank verlangt dafür bei -prozentiger Verzinsung € Zinsen. Wie hoch war der Kredit?
Der Kredit hatte eine Höhe von €.
richtig: 0falsch: 0
Aufgabe 17: Trage die fehlenden Zeitangaben ein. Rechne zuerst den Jahreszins aus. Nach dem fünften falschen Eintrag wird die Lösung angezeigt.
| Kapital | Zinssatz | Zinsen für Zeitraum | |
| Monate | |||
| Tage | |||
richtig: 0falsch: 0
Aufgabe 18: Eric kann 4200 € auf seinem Sparbuch mit 3 % verzinsen. Von den Zinsen möchte er sich ein Geschenk kaufen, das 73,50 € kostet. Wie lange muss er sein Geld anlegen, damit das klappt?
Nach Monaten kann Eric sich das Geschenk von seinen Zinsen kaufen.
richtig: 0falsch: 0
Aufgabe 19: Klick die richtigen Ergebnisse an. Die Dreisätze und Formeln können als Hilfe dienen.
| 1 Zinsjahr = 360 Tage | 1 Zinsmonat = 30 Tage | = | Z · 360 · 100 |
| t · p |
|
Anzahl: | ges: K | p% | t (M) | Z |
|
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
Aufgabe 20: Herr Winnefeld benötigt einen Kredit in Höhe von 26 000 € für 9 Monate. Von zwei Banken bekommt er ein Angebot. Für welches sollte er sich entscheiden?
|
SparBank-Privatkredit 4,8 % keine |
Volkskasse-Sofortkredit 4,5 % Bearbeitungsgebühr |
Herr Winnefeld sollte sich für das Angebot der , denn so spart er €.
Versuche: 0
Aufgabe 21: Frau Schneider nimmt einen Kredit in Höhe von 124 000 € auf. Die Bank verlangt 4,5 % Zinsen.
a) Wie hoch sind die Zinsen nach 235 Tagen?
b) Wie viel Euro muss sie insgesamt zurückzahlen?
a) Die Zinsen betragen €.
b) Insgesamt muss sie € zurückzahlen.
richtig: 0falsch: 0
Aufgabe 22: Herr Scheffel hat sein Girokonto Tage überzogen. Bei einem Zinssatz von 11,5 % muss er 5,75 € bezahlen. Um wie viel Euro war sein Konto überzogen?
Herr Scheffel überzog sein Konto um €.
richtig: 0falsch: 0
Aufgabe 23: Klick auf die Zahlen und trage die richtigen Begriffe ein.
|
Lösungssilben: BATT | DIT | GI | HY | KA | KON | KRE | PI | PO | RA | RO | SATZ | SEN | SKON | TAL | THEK | TO | TO | ZIN | ZINS
Aufgabe 24: Ordne die Zahlen der Tabelle so zu, dass die Daten jeder Zeile stimmig sind.
| Kapital | Zinssatz |
Zeit |
Zinsen |
|
| a) | 2200 € |
|||
| b) | 5,4 % | |||
| c) | 180 t | |||
| d) | 59,50 € |
Versuche: 0
Aufgabe 25: Welcher jährliche Zinssatz liegt der Ratenzahlung zugrunde? Eine Bearbeitungsgebühr wird nicht erhoben.
 |
Die Ratenzahlung wird mit einem Zinssatz von % verzinst.
Versuche: 0
Aufgabe 26: Für ein Darlehen muss Frau Nolte nach 240 Tagen Zinsen in Höhe von 2952 € zahlen. Der Zinssatz des Darlehens betrug 5,4 %.
a) Berechne das Darlehen.
b) Wie hoch ist der Rückzahlungsbetrag?
a) Das Darlehen hatte eine Höhe von €.
b) Insgesamt wurden € zurückgezahlt.
richtig: 0falsch: 0
Aufgabe 27: Herr Glück hat eine Erbschaft so angelegt, dass er von den Zinseinnahmen leben kann. Vierteljährig bekommt er von seiner Bank ausbezahlt. Das geerbte Geld ist mit verzinst. Wie groß war die Erbschaft?
Herr Glück hat € geerbt.
richtig: 0falsch: 0
Aufgabe 28: Auf Haralds Guthaben von 4 500 € zahlt die Bank 3,1 % Zinsen. Einige Zeit später werden 4569,75 € ausgewiesen.
a) Wie hoch waren die Zinsen.
b) Wie lange war das Geld angelegt?
a) Die Zinsen betrugen €.
b) Das Geld war Tage lang angelegt.
richtig: 0falsch: 0
Aufgabe 29: Ein Kapital von 9 600 € wurde 6 Monate lang mit 5 % verzinst. Welcher Zinssatz bringt genauso viele Zinsen in 8 Monaten ein?
Wenn das Kapital zu % verzinst ist, bringt es nach 8 Monaten die gleichen Zinsen.
richtig: 0falsch: 0
Aufgabe 30: Pia und Frank haben gleich viel Geld angelegt. Pia zu 3,2 % und Frank zu 3,8 %. Nach einem Jahr erhält Frank 33 € mehr Zinsen als Pia. Welchen Betrag haben die beiden anfänglich jeweils angelegt?
Jeder der beiden hat € angelegt.
richtig: 0falsch: 0
Aufgabe 31: Heikos Sparkonto veränderte sich folgendermaßen: Zu Jahresanfang besaß er 1500 € Guthaben. Nach 3 Monaten zahlte er weitere 900 € ein. Nach weiteren 2 Monaten kamen noch einmal 600 € hinzu. 4 Monate später zog er jedoch 1100 € vom Konto ab. Wie viele Zinsen wurden im nach Ablauf eines Jahres gutgeschrieben, wenn das Konto mit 3% verzinst war?
Insgesamt kamen in diesem Jahr Zinsen von € zustande.
richtig: 0falsch: 0
Aufgabe 32: Frau Schilling hat ihr Haus mit zwei Hypotheken belastet. Die erste Hypothek umfasst zu , die zweite zu . Sie möchte beide Hypotheken durch eine so ersetzen, dass sie für die neue die gleichen Jahreszinsen zu bezahlen hat, wie für die beiden alten. Welchen Zinssatz müsste diese Hypothek haben?
Die neue Hypothek hat einen Zinssatz von %.
richtig: 0falsch: 0
Aufgabe 33: Hendrik und Sabine legen gleich viel Kapital an. Hendrik legt sein Geld zu und Sabine die gleiche Summe zu an. Zählt man die erreichten Zinsen der beiden zusammen, erhält man eine Summe von . Welches Kapital haben Hendrik und Sabine anfänglich jeweils eingesetzt?
|
|||
|
Jeder der beiden hat anfänglich eine Kapital von € angelegt.
richtig: 0falsch: 0
Ratenkredit
Ein Ratenkredit ist geliehenes Kapital, dass in gleichmäßigen Raten zurückgezahlt wird. Die Höhe der Raten richtet sich nach folgenden Punkten:
- Tilgungsdauer (Zeitraum der Rückzahlung)
- Zinsen (Monatlicher Zinssatz "p. m.", der sich immer auf die ursprüngliche Kredithöhe bezieht.)
|
Beispiel:
Kreditsumme: 12 000 € Rechnung: |
|||
| Zinsen pro Monat: | |||
| 0,5 % von 12 000 € | = | 60 € | |
| Kreditsumme: | = | 12 000 € | |
| Gesamtzinsen: | |||
| + 60 € · 24 | = | 1 440 € | |
| Rückzahlungsbetrag: | 13 440 € | ||
| Monatliche Rate: | |||
| 13 440 € : 24 | = | 560 € | |
Aufgabe 34: Berechne die Gesamtzinsen, den Rückzahlungsbetrag und die monatliche Rate. Achtung! Der Zinssatz bezieht sich auf die gesamte Laufzeit. Die Monatsraten wurden jedoch auf Kundenwunsch auf ganze Euro aufgerundet, so dass die letzte Monatsrate sich von den übrigen mit der Bank vereinbarten Raten unterscheidet.
|
Kreditsumme: € Zinssatz: % p. m. Laufzeit: Monate |
|||
| Kreditsumme: | € | ||
| Gesamtzinsen | + | € | Rückzahlungsbetrag: | € |
| Monatliche Rate: | € | ||
| Letzte Monatsrate: | LMR € | ||
richtig: 0 | falsch: 0
Aufgabe 35: Frau Winkler nimmt einen Ratenkredit in Höhe von auf. Sie will ihn in gleichmäßigen Monatsraten bei einem Zinssatz von pro Monat zurückzahlen. Die Bank verlangt eine einmalige Bearbeitungsgebühr von 0,5 %.
a) Wie viel Euro muss sie insgesamt zurückzahlen?
b) Wie hoch sind die gleichmäßigen Monatsraten?
a) Sie zahlt insgesamt € zurück.
b) Eine Monatsrate beträgt €.
richtig: 0falsch: 0
Aufgabe 36: Autohaus Odentaler bietet für den Kauf eines PKW folgendes Kreditangebot:
|
a) Wie hoch ist der Kreditbetrag? b) Wie viele Zinsen fallen an? c) Wie hoch ist der monatliche Zinssatz? |

|
a) Der Kredit hat eine Höhe von €.
b) Es fallen € Zinsen an.
c) Der Zinssatz beträgt % p. m.
Versuche: 0

