Grundwert
Der Grundwert gibt das Ganze (100 %) an.
Aufgabe 1: Ziehe die orangen Gleiter der unteren Grafik und beobachte, wie sich Beispielaufgabe, Dreisatz und Formel verändern.
Der Prozentsatz der folgenden Beispiele ist gerundet.
- Beispielaufgabe: Du hast 60 € an einen Freund verliehen. Das sind 30 % deines Guthabens. Wie viel Euro beträgt dein ganzes Guthaben?
Antwort: Du hast ein Guthaben von 200 €. Der Grundwertwert beträgt 200 €.
-
Dreisatz: : 30 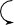
30 % ≙ 60 € 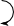 : 30
: 301 % ≙ 2 € · 100 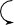
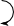 · 100
· 100100 % ≙ 200 €
-
Formel: G = P · 100 = 60 € · 100 = 200 € p 30
Aufgabe 2: Passe die oberen Grafikdaten durch das Ziehen der orangen Punkte den jeweiligen Daten einer Tabellenzeile an und trage den entsprechenden Prozentwert an die richtige Stelle ein.
| Leihgabe in € | Leihgabe in % | Grundwert |
| 90 € | 60 % | € |
| 96 € | 60 % | € |
| 102 € | 60 % | € |
| 117 € | 60 % | € |
Versuche: 0
Aufgabe 3: Trage die fehlenden Grundwerte in die Tabelle ein.
| G | € | € | € | € | € |
| p | 15 % | 22 % | 37 % | 18 % | 65 % |
| P | 360 € | 253 € | 878,75 € | 359,82 € | 2267,85 € |
Versuche: 0
Aufgabe 4: Klick die Werte so an, dass immer der gleiche Grundwert entsteht. Trage den gesuchten Grundwert in das entsprechende Textfeld ein.
| — | 98 % | |||
| — | 3 % | |||
ist |
50 % | von |
||
| — | 24 % | |||
| — | 10 % |
Versuche: 0
Aufgabe 5: Berechne den fehlenden Grundwert mit Hilfe des Dreisatzes.
| Spalte 2 |
|
|
Aufgabe 6: Trage die fehlenden Grundwerte ein.
|
a) b) c) |
richtig: 0falsch: 0
Aufgabe 7: In der letzten Mathematikarbeit hatten 9 Schüler ein "gut". Das waren 30% aller Schüler. Wie viele Schüler hat die Klasse?
Die Klasse besteht aus Schülern.
Versuche: 0
Aufgabe 8: Bei einem Laufwettbewerb erreichten 1868 Läufer das Ziel. 20% der Teilnehmer schieden vorher aus. Wie viele Läufer sind bei diesem Wettbewerb gestartet?
An diesem Wettbewerb haben Läufer teilgenommen.
Versuche: 0
Aufgabe 9: Meerwasser hat einen Salzgehalt von 3,5 %. Aus wie viel kg Meerwasser lassen sich 77 g Salz gewinnen?
Dafür benötigt man kg Meerwasser.
Versuche: 0
Erhöhter (vermehrter) und verminderter Grundwert
Erhöht ist ein Grundwert, wenn ihm ein bestimmter Prozentsatz seines ursprünglichen Wertes hinzugefügt wurde.
GErh = G + (x% von G)Vermindert ist ein Grundwert, wenn von ihm ein bestimmter Prozentsatz seines ursprünglichen Wertes abgezogen wurde.
GVerm = G - (x% von G)In Aufgabenstellungen wird oft der um einen bestimmten Prozentsatz erhöhte oder verminderte Grundwert angegeben und der ursprüngliche Grundwert muss dann berechnet werden.
Aufgabe 10: Klick verschiedene Prozentangaben in den unteren Spaltentexten an. Finde den jeweiligen Grundwert heraus und trage ihn in das Textfeld der mittleren Skala ein. Nach der fünften falschen Eingabe wird die Lösung angezeigt.
|
Erhöhter Ein Preis
Jetzt beträgt Wie hoch war |
Erhöhter |
|
Grund- 100 % |
|
Vermind. |
Verminderter Ein Preis ver- Jetzt beträgt Wie hoch war |
richtig: 0falsch: 0
Aufgabe 11: Klick die richtigen Begriffe an.
|
Versuche: 0
| Rechenweg A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
vom Grundwert Beispiel: 5 % Rabatt Rabattpreis: 100 % - 5 % = 95 % |
vom Grundwert Beispiel: 19 % MwSt Bruttopreis: 100 % + 19 % = 119 % |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dreisatz Ladenpreis = 300 €
Rabattpreis = 285 € |
Dreisatz Nettopreis = 300 €
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Rechenweg B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
vom verminderten
Grundwert Beispiel: Rabattpreis → 95 % Ladenpreis: 95 % + 5 % = 100 % |
vom erhöhten
Grundwert Beispiel: Bruttopreis → 119 % Nettopreis: 119 % - 19 % = 100 % |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dreisatz Rabattpreis = 285 €
Ladenpreis = 300 € |
Dreisatz Bruttopreis = 357 €
Nettopreis = 300 € |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Achtung! Häufig tritt bei diesen Rechnungen folgender Fehler auf: Die gestellte Aufgabe sollte eigentlich nach Rechenweg B gelöst zu werden, an die erste Stelle des Dreisatzes wird aber nicht der benötigte verminderte oder erhöhte Grundwert eingesetzt, sondern 100 %. Das führt zu einem falschen Ergebnis.
Aufgabe 12: Die ursprünglichen Grundwerte wurden um den jeweils aufgeführten Wert vermindert oder vermehrt. Gib den entsprechenden Prozentsatz des verminderten oder vermehrten Grundwerts an.
Bsp: Grundwert vermindert um 2 % → verminderter Grundwert: 98 %
Grundwert vermindert um % → verminderter Grundwert: %
Grundwert vermehrt um % → vermehrter Grundwert: %
Grundwert um % → Grundwert: %
richtig: 0falsch: 0
Aufgabe 13: Trage den gesuchten Prozentsatz ein.
| Prozentsatz früher | Entwicklung | Prozentsatz heute |
| 100 % | % |
richtig: 0falsch: 0
Aufgabe 14: Trage die erhöhten Grundwerte ein.
|
Grund- wert |
neuer Prozentsatz |
erhöhter Grundwert |
| m | % | m |
| kg | % |
kg |
| l | % | l |
richtig: 0falsch: 0
Aufgabe 15: Trage die verminderten Grundwerte ein.
|
Grund- wert |
neuer Prozentsatz |
verminderter Grundwert |
| m | % | m |
| € | % |
€ |
| t | % | t |
richtig: 0falsch: 0
Aufgabe 16: Im Jahr wurden in einem Naturschutzgebiet Vögel gezählt. Das waren als im Vorjahr. Wie viele Vögel wurden ermittelt? Trage die Lösung über dem entsprechenden Datum ein.
 |
||
richtig: 0falsch: 0
Aufgabe 17: Trage die ursprünglichen Grundwerte ein.
|
Grund- wert |
neuer Prozentsatz |
erh./verm. Grundwert |
| cm | % | cm |
| t | % | t |
| m² | % | m² |
richtig: 0falsch: 0
Aufgabe 18: Trage den Grundwert vor der Erhöhung ein.
| Erhöhter Wert | € | € | € |
| Erhöhung um | % | % | % |
| Grundwert | € | € | € |
richtig: 0falsch: 0
Aufgabe 19: Trage den Grundwert vor der Verminderung ein.
| Verminderter Wert | € | € | € |
| Verminderung um | % | % | % |
| Grundwert | € | € | € |
richtig: 0falsch: 0
Aufgabe 20: Trage die fehlenden Werte ein.
| Grundwert | neuer Prozentsatz |
erh./verm. Grundwert |
| % | ||
richtig: 0falsch: 0
Aufgabe 21: In den angegebenen Preisen unten sind 19 % Mehrwertsteuer enthalten oder abgezogen. Trage die entsprechend richtigen Preise ohne Nachkommastellen ein.
| mit MwSt | ohne MwSt | mit MwSt | ohne MwSt | |
| 238 € | € | 476 € |
€ | |
| 1547 € |
€ |
833 € | € |
|
| € |
5400 € | € |
2100 € |
|
| € |
4300 € |
€ |
1200 € |
Versuche: 0
Aufgabe 22: Ergänze die fehlenden Größen.
|
a) |
b) |
|
| Einkaufspreis |
€ | 800 € |
| Geschäftskosten |
5 % | % |
| Selbstkosten |
€ | 920
€ |
| Gewinn in % |
15
% |
% |
| Verkaufspreis |
€ |
1012
€ |
| MwSt. in % |
19
% |
% |
| Endpreis |
3448,62
€ |
1204,28 € |
Versuche: 0
Aufgabe 23: Trage die fehlenden Werte ein. Bestimme vorher, welche Werte gegeben sind, bzw. welchem Prozentsatz diese Werte entsprechen.
| Netto | Brutto (inkl. 19% MwSt) |
MwSt-Betrag | Endbetrag (2% Skonto) |
|
| a) | € | € | € | |
| b) | € | € | € | |
| c) | € | € | € | |
| d) | € | € | € |
richtig: 0falsch: 0
Aufgabe 24: Ordne zu, welche Größe (x) jeweils berechnet wird.
Aufgabe 25: Die Schule am Park wurde im letzten Jahr von 650 Schülerinnen und Schülern besucht. In diesem Jahr sind es 8 % mehr. Wie hoch ist die Schülerzahl jetzt?
Zur Zeit besuchen Schüler und Schülerinnen die Schule.
Versuche: 0
Aufgabe 26: Auf einer Apfelsaftpackung steht: "Jetzt 10% mehr Inhalt." Vorher enthielt die Packung 1 Liter Saft. Wie viel Saft ist jetzt in der Packung?
Es befinden sich Liter Saft in der Packung.
Versuche: 0
Aufgabe 27: Im vergangenen Jahr übernachteten 38400 Gäste in einem Feriendorf. Dieses Jahr ist die Zahl der Übernachtungen um 9 % zurückgegangen. Wie viele Übernachtungen sind es dieses Jahr?
Die Anzahl der Übernachtungen beträgt im aktuellen Jahr .
Versuche: 0
Aufgabe 28: Eine Kiste mit einem schweren Arbeitsgerät wiegt 350 kg. Das Gerät selbst wiegt 301 kg. Wie viel Prozent des Gesamtgewichts wiegt der Apparat?
Das Arbeitsgerät wiegt % des Gesamtgewichts.
Versuche: 0
Aufgabe 29: Ein Sportgeschäft verkaufte 308 Skateboards in einem Jahr. Das waren 12 % weniger als im Jahr davor. Wie viele Skateboards wurden im Vorjahr verkauft?
Im Vorjahr wurden Skateboards verkauft.
Versuche: 0
Aufgabe 30: Durch eine Werbeaktion gelang es einem Sportverein, seine Mittglieder innerhalb eines Jahres auf Personen zu steigern. Das entsprach einer Steigerung von %. Wie viele Mitglieder hatte der Verein letztes Jahr?
Letztes Jahr bestand der Verein aus Mitgliedern.
richtig: 0falsch: 0
Aufgabe 31: Ein Elektroartikel wird nach einer Preissenkung von % für € angeboten. Wie viele Geld hat das Gerät vorher gekostet?
Der Artikel wurde vorher für € verkauft.
richtig: 0falsch: 0

Aufgabe 32: Timo möchte sich einen Karateanzug kaufen. Zwei kommen für ihn in die engere Wahl. Der Anzug aus der Vorjahreskollektion kostete früher 75 € und wurde um 12 % reduziert. Der Anzug aus der aktuellen Kollektion übersteigt den Ursprungspreis des ersten Anzugs um 8 %. Wie viel Geld spart Timo, wenn er sich den älteren Anzug kauft?
Timo spart € wenn er den Anzug vom letzten Jahr kauft.
Versuche: 0

