Teilbarkeit
- Vielfache (A 1 - A 9),
- Teiler (A 10 - A 16),
- Primzahlen (A 17 - A 26),
- Teilbarkeitsregeln (A 27 - A 42),
- Größter gemeinsamer Teiler (A 52 - A 56),
- Kleinstes gemeinsames Vielfaches (A 57 - A 62)
Vielfache
Die Zahlen 4, 8, 12, 16, ... nennt man Vielfache der Zahl 4. Die Vielfachen einer Zahl schreibt man
- lang
Vielfache von 4: 4, 8, 12, 16, 20, 24 ... - kurz
V4: 4, 8, 12, 16, 20, 24 ...
Aufgabe 1: Klick auf neu und betrachte, wie du die Vielfachen einer größeren Zahl geschickt berechnen kannst.
| Schritt 1: | · 10 | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | -fach | |
| Schritt 2: | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | -fach | |
| Schritt 3: | · 2 | · 2 | · 2 | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | -fach | ||||
| Schritt 4: | + | + | + | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | -fach | ||
Aufgabe 2:Gib die ersten fünf Vielfachen der Zahlen an.
| a) V: {, , , , ...} |
| b) V: {, , , , ...} |
| c) V: {, , , , ...} |
richtig: 0falsch: 0
Aufgabe 3: Trage das Zehnfache und das Fünffache von 10 ein.
10-fach |
5-fach |
||
| 10 · 10 = | ; | : 2 = |
richtig: 0falsch: 0
Aufgabe 4: Trage das Doppelte, das Vierfache und das Achtfache von 10 ein.
2-fach |
4-fach |
8-fach |
|||
| 10 · 2 = | ; | · 2 = | ; | · 2 = |
richtig: 0falsch: 0
Aufgabe 5: Zwei Zahlen in jeder Vielfachreihe sind falsch. Ersetze sie durch die richtigen.
| V2: {, , , , , , , , , ...} |
| V3: {, , , , , , , , , ...} |
| V4: {, , , , , , , , , ...} |
| V5: {, , , , , , , , , ...} |
| V6: {, , , , , , , , , ...} |
| V7: {, , , , , , , , , ...} |
| V8: {, , , , , , , , , ...} |
| V9: {, , , , , , , , , ...} |
richtig: 0falsch: 0
Aufgabe 6: Klick auf den richtigen Buzzer. Ist die Aussage richtig oder falsch?
| a)1x | b)10x |
3 ist Vielfaches von 12 |
|
• |
• |
|
a) richtig: 0falsch: 0 b) richtig: 0falsch: 0 |
|
Aufgabe 7: Trage die richtigen Werte ein.
| a) V11: {, ,33 , ...} |
| b) V: {13, 26, , , ...} |
| c) V: {, , 51, 68, ...} |
| d) V: {, , , 160, ...} |
Versuche: 0
Aufgabe 8: Trage die richtigen Werte aus dem Schaubild der Reihe nach von links nach rechts ein.
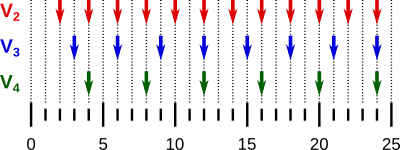
| Vielfache von 2 und 3: {, , , ...} |
| Vielfache von 2 und 4: {, , , , , ...} |
| Vielfache von 2, 3 und 4: {, ...} |
Versuche: 0
Aufgabe 9: Trage zwei unterschiedliche Zahlen ein, die größer als 30 und sowohl Vielfache von 4 und von 5 sind.
V4 ∧ V5 ∧ > 30
a) b)
richtig: 0 | falsch: 0
Teiler
Die Zahlen 1, 2, 3, 5, 6, 10, 15 und 30 sind Teiler von 30
- lang
Teiler von 30: {1, 2, 3, 5, 6, 10, 15, 30} - kurz
T30: {1, 2, 3, 5, 6, 10, 15, 30}
Aufgabe 10: Lea möchte aus 24 Würfeln gleich hohe Türme bauen. Welche Möglichkeiten hat sie, wenn immer alle Würfel verbaut werden sollen?
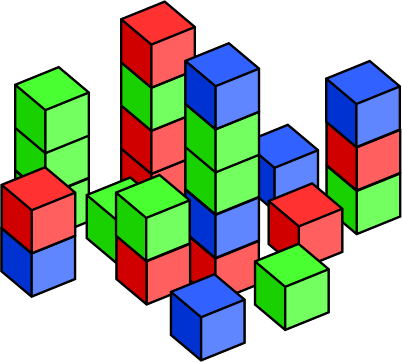
| Anzahl der Türme | 1 | 3 | 4 | 8 | 12 | |||
| Würfelanzahl je Turm | 12 | 6 | 4 | 1 |
Versuche: 0
Aufgabe 11: Das bläuliche Rechteck beinhaltet 16 Quadrate, die in 2 Spalten und 8 Zeilen angeordnet sind. In welche Spalten- und Zeilenanordnungen finden ebenfalls genau 16 Quadrate Platz? Probiere es aus, indem du auf das bläuliche Rechteck klickst und seine Größe veränderst.
| Anzahl der Spalten | 1 | 2 | 16 | ||
| Anzahl der Zeilen | 8 | 2 |
Versuche: 0
Aufgabe 12: Trage die passenden Zerlegung der grünen Zahlen in die darunterliegenden Felder ein.
20 |
30 |
|||
| 4 · | 5 · | · 10 | · 3 | |
| 2 · | 10 · | 2 · | 15 · | |
| 1 · | 20 · | · 30 | · 1 | |
Versuche: 0
Info: Die Zahl 12 kann durch 1, 2, 3, 4, 6 und 12 geteilt werden. Dies sind die Teiler von 12. Man sagt: "4 ist Teiler von 12."
Aufgabe 13: Klick auf den richtigen Buzzer. Ist die Aussage richtig oder falsch?
| a)1x | b)10x |
3 ist Teiler von 12 |
|
• |
• |
|
a) richtig: 0falsch: 0 b) richtig: 0falsch: 0 |
|
Aufgabe 14: Klicke auf die Felder, bei denen die Zahl der Randspalte Teiler der Zahl in der Kopfzeile ist.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | ||||||||||||
| 2 | ||||||||||||
| 3 | ||||||||||||
| 4 | ||||||||||||
| 5 | ||||||||||||
| 6 | ||||||||||||
| 7 | ||||||||||||
| 8 | ||||||||||||
| 9 | ||||||||||||
| 10 | ||||||||||||
| 11 | ||||||||||||
| 12 |
richtig: 0 | falsch: 0
Aufgabe 15: Trage zwei unterschiedliche Zahlen ein, die größer als 30 und sowohl durch 4 und durch 5 teilbar sind.
a) b)
richtig: 0 | falsch: 0
Aufgabe 16: Trage die Teiler der folgenden Zahlen der Größe nach in die Textfelder ein. Fange mit dem kleinsten Teiler an.
| a) T26: | {, , , } |
| b) T47: | {, } |
| c) T67: | {, } |
| d) T88: | {, , , , , , , } |
| e) T145: | {, , , } |
Versuche: 0
Primzahlen
Primzahlen haben genau zwei Teiler. Sie sind nur durch 1 und sich selbst teilbar. Die Primzahlen bis 30 heißen: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Die Zahl 1 ist keine Primzahl, denn sie hat nur einen Teiler.
Aufgabe 17: Trage den Begriff ein, den die Buchstaben neben den Primzahlen ergeben.
| 31 | K | 37 | N | 39 | A | 40 | R | |||
| 41 | O | 42 | G | 43 | B | 45 | U | |||
| 47 | E | 50 | R | 52 | O | 53 | L | |||
| 55 | S | 56 | T | 59 | E | 61 | I | |||
Lösungswort:
Versuche: 0
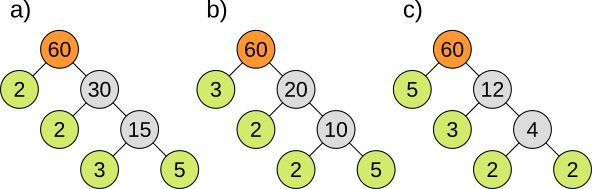
Mittels Faktorenbaum kann eine Zahl so lange in Faktoren zerlegt werden, bis am Ende nur noch Primzahlen stehen. Beispiel:
| a) 60 = 2 · 30 | 30 = 2 · 15 | 15 = 3 · 5 | 2 · 2 · 3 · 5 = 60 |
| b) 60 = 3 · 20 | 20 = 2 · 10 | 10 = 2 · 5 | 3 · 2 · 2 · 5 = 60 |
| c) 60 = 5 · 12 | 12 = 3 · 4 | 4 = 2 · 2 | 5 · 3 · 2 · 2 = 60 |
Aufgabe 18: Ergänze den Faktorenbaum richtig.
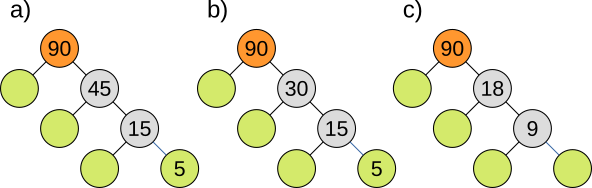 |
Versuche: 0
Aufgabe 19: Ergänze den Faktorenbaum richtig.
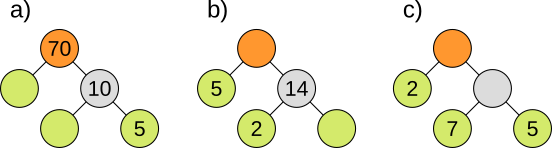 |
Versuche: 0
Aufgabe 20: Ergänze den Faktorenbaum richtig.
 |
Versuche: 0
Aufgabe 21: Ergänze die Ergebnisse der Primfaktorenreihe.
2 · 2 = ; · 2 = ; · 2 = ; · 2 = ; · 2 =
Versuche: 0
Aufgabe 22: Ergänze die Ergebnisse der Primfaktorenreihe.
3 · 2 = ; · 2 = ; · 2 = ; · 2 = ; · 2 =
Versuche: 0
Aufgabe 23: Ergänze die Ergebnisse der Primfaktorenreihe.
3 · 3 = ; · 2 = ; · 2 = ; · 2 =
Versuche: 0
Aufgabe 24: Ergänze die Ergebnisse der Primfaktorenreihe.
3 · 3 = ; · 3 = ; · 2 =
Versuche: 0
Aufgabe 25: Trage der Reihe nach alle fehlenden Zahlen unter 30 ein, die aus Multiplikationen mit den Primfaktoren 2, 3, und 5 gebildet werden können (Beispiel: 2 · 2 = 4, 2 · 3 · 5 = 30).
4, , , , , , , 16, , , , , , 30
Versuche: 0
Aufgabe 26: Es gibt die Goldbach-Vermutung, das man alle gerade Zahlen als Summe von zwei Primzahlen darstellen kann. Versuche es.
+ =
richtig: 0 | falsch: 0
Aufgabe 27: Markiere die Zellen, bei denen der Wert aus der oberen Zeile durch den jeweiligen Wert der linken Spalte ohne Rest geteilt werden kann.
| 14 | 15 | 16 | 20 | 21 | 25 | 27 | 30 | 32 | 35 | 38 | 40 | |
| teilbar durch 2 | ||||||||||||
| teilbar durch 5 | ||||||||||||
| teilbar durch 10 |
richtig: 0 | falsch: 0
Aufgabe 28: Wähle die richtigen Ziffern aus.
Eine Zahl ist teilbar
Versuche: 0 |
Aufgabe 29: Klicke alle Zahlen an, die durch 2 teilbar sind.
a) b) c) d) e) f)
richtig: 0 | falsch: 0
Aufgabe 30: Klicke alle Zahlen an, die durch 5 teilbar sind.
a) b) c) d) e) f)
richtig: 0 | falsch: 0
Aufgabe 31: Trage die nächstgrößere durch 5 teilbare Zahl ein.
a) ▸ b) ▸ c) ▸
richtig: 0falsch: 0
Aufgabe 32: Trage die nächstkleinere durch 5 teilbare Zahl ein.
a) ▸ b) ▸ c) ▸
richtig: 0falsch: 0
Aufgabe 33: Klicke alle Zahlen an, die durch 10 teilbar sind.
a) b) c) d) e) f)
richtig: 0 | falsch: 0
Aufgabe 34: In der Tabelle ist die Teilbarkeit einiger Zahlen angegeben. Trage die richtigen Werte in die Lücken ein.
| 324 | 335 | 342 | 360 | |
| teilbar durch | X | X | ||
| teilbar durch | X | |||
| teilbar durch | X | X | X | |
| teilbar durch | X | X |
Versuche: 0
Aufgabe 35: Die folgenden Zahlen sollen durch 4 teilbar sein. Setze dafür eine richtige Ziffer in die Lücke ein.
| a) | 642 | b) | 35 | c) | 534 |
| d) | 12 | e) | 268 | f) | 376 |
| g) | 748 | h) | 248 | i) | 13 |
Versuche: 0
Aufgabe 36: Die folgenden Zahlen sollen durch 8 teilbar sein. Setze dafür eine richtige Ziffer in die Lücke ein.
| a) | 516 | b) | 326 | c) | 738 |
| d) | 142 | e) | 451 | f) | 668 |
| g) | 874 | h) | 281 | i) | 999 |
Versuche: 0
Aufgabe 37: Klicke auf die Felder, bei denen die Zahl der Randspalte Teiler der Zahl in der Kopfzeile ist.
| 150 | 260 | 275 | 300 | 325 | 540 | 550 | 557 | 600 | |
| teilbar durch 20 | |||||||||
| teilbar durch 25 | |||||||||
| teilbar durch 50 | |||||||||
| teilbar durch 100 |
richtig: 0 | falsch: 0
Aufgabe 38: Wähle die richtigen Ziffern aus.
Eine Zahl ist teilbar
Versuche: 0 |
Aufgabe 39: Klick auf den richtigen Buzzer. Ist die Aussage richtig oder falsch?
| a)1x | b)10x |
• |
• |
|
a) richtig: 0falsch: 0 b) richtig: 0falsch: 0 |
|
Quersummenregel
Aufgabe 40: Wenn alle Ziffern einer Zahl miteinander addiert werden, erhält man ihre Quersumme. Solange das Ergebnis dieser Addition eine mehrstellige Zahl ist, kann von der Quersumme abermals die Quersumme ermittelt werden. Klicke unten auf den Button "Quersumme" und betrachte, was damit gemeint ist.
5 + 5 + 5 + 5 + 55 + 5 = 5
Aufgabe 41: Trage die Quersummen der Zahlen aus der ersten Reihe an entsprechender Stelle ein. Markiere danach mit einem Häkchen ✔, ob die Quersumme durch 3 beziehungsweise durch 9 teilbar ist.
| Zahl | 27 | 28 | 30 | 31 | 33 | 36 | 38 | 42 | 45 |
| Quersumme | |||||||||
| teilbar durch 3 | |||||||||
| teilbar durch 9 |
Versuche: 0
Aufgabe 42: Klicke alle Zahlen an, die durch 3 teilbar sind.
a) b) c) d) e) f)
richtig: 0 | falsch: 0
Aufgabe 43: Klicke alle Zahlen an, die durch 9 teilbar sind.
a) b) c) d) e) f)
richtig: 0 | falsch: 0
Aufgabe 44: Trage die nächstgrößere durch 9 teilbare Zahl ein.
a) ▸ b) ▸ c) ▸
richtig: 0falsch: 0
Aufgabe 45: Trage die nächstkleinere durch 9 teilbare Zahl ein.
a) ▸ b) ▸ c) ▸
richtig: 0falsch: 0
Aufgabe 46: Die folgenden Zahlen sollen durch 9 teilbar sein. Setze dafür eine richtige Ziffer in die Lücke ein.
| a) | 16 | b) | 25 | c) | 38 |
| d) | 472 | e) | 551 | f) | 698 |
| g) | 798 | h) | 836 | i) | 999 |
Versuche: 0
Aufgabe 47: Klicke auf die Felder, bei denen die Zahl der Randspalte Teiler der Zahl in der Kopfzeile ist.
| 30 | 33 | 36 | 38 | 43 | 45 | 46 | 48 | 50 | |
| teilbar durch 2 | |||||||||
| teilbar durch 3 | |||||||||
| teilbar durch 6 |
richtig: 0 | falsch: 0
Aufgabe 48: Wähle die richtigen Werte aus.
Eine Zahl ist teilbar
Versuche: 0 |
Aufgabe 49: Klick auf den richtigen Buzzer. Ist die Aussage richtig oder falsch?
| a)1x | b)10x |
• |
• |
|
a) richtig: 0falsch: 0 b) richtig: 0falsch: 0 |
|
Aufgabe 50: Trage die gültigen Lösungen ein.
| a) | Eine Zahl, die zwischen 130 und 140 liegt und durch 9 teilbar ist: |
| b) | Eine Zahl, die zwischen 330 und 340 liegt und durch 3 und 4 teilbar ist: |
| c) | Die kleinste dreistellige Zahl, die durch 2 und 3 teilbar ist: |
| d) | Eine dreistellige Zahl, die auf 43 endet und mit 9 teilbar ist: |
Versuche: 0
Aufgabe 51: Starte das Spiel und klicke auf die jeweils neu angegebene Zahl.
|
Klick auf eine Zahl, die durch teilbar ist. |
 046
146  246  346  446  

|
richtig: 0 | falsch: 0 |
Größter gemeinsamer Teiler (ggT)
Der größte gemeinsame Teiler (ggT) kann unterschiedliche bestimmt werden.
Beispiel: ggT von 36 und 54
|
A) Die gemeinsamen Teiler suchen und den größten finden.  T36: 1, 2, 3, 4, 6, 9, 12, 18, 36 T54: 1, 2, 3, 6, 9, 18, 27, 54 ggT(36, 54): 18 |
||||||||||||||||||||||||
|
B) Gemeinsame Primfaktoren suchen und miteinander multiplizieren..
|
||||||||||||||||||||||||
Aufgabe 52: In folgenden Schritten erhält man den ggT mithilfe der Primfaktorzerlegung. Trage die richtigen Begriffe in den Text ein.
- Zerlege alle Zahlen für die Bestimmung des ggTs in ihre (keimPratorfn).
- Schreibe gleiche Primfaktoren (einteranduner).
- Kommen in einer (alteSp) die gleichen Primfaktoren vor, so (rotiene) diese.
- (zultipliMiere) die spaltenweise vorkommenden Primfaktoren.
Versuche: 0
Aufgabe 53: Trage jeweils den größten gemeinsamen Teiler (ggT) der zwei Werte ein.
| a) ggT = |
| b) ggT = |
| c) ggT = |
richtig: 0falsch: 0
Aufgabe 54: Der folgende Karton wird lückenlos mit gleichgroßen Würfeln gefüllt. Welches ist die größte Kantenlänge, die ein Würfel haben kann?

Die größte Kantenlänge eines Würfels beträgt cm
Versuche: 0
Aufgabe 55: Trage jeweils den größten gemeinsamen Teiler (ggT) der zwei Werte ein.
| a) ggT = |
| b) ggT = |
| c) ggT = |
richtig: 0falsch: 0
Aufgabe 56: Trage jeweils den größten gemeinsamen Teiler (ggT) der drei Werte ein.
| a) ggT = |
| b) ggT = |
| c) ggT = |
richtig: 0falsch: 0
Kleinstes gemeinsames Vielfaches (kgV)
|
A) Unter den gemeinsamen Vielfachen das kleinste suchen. 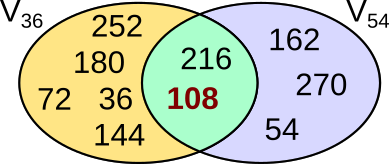 V36: 36, 72, 108, 144, 180, 216, 252 ... V54: 54, 108, 162, 216, 270 ... kgV(36, 54): 108 |
||||||||||||||||||||||||
|
B) Primfaktoren die mehrfach vorkommen einfach multiplizieren.
|
||||||||||||||||||||||||
Aufgabe 57: In folgenden Schritten erhält man den kgV mithilfe der Primfaktorzerlegung. Trage die richtigen Begriffe in den Text ein.
- Zerlege alle Zahlen für die Bestimmung des kgVs in ihre (keimPratorfn).
- Notiere alle Primfaktoren. Kommen Faktoren mehrfach vor, zähle die Stelle (eichnaf).
- (zultipliMiere) alle Faktoren.
Versuche: 0
Aufgabe 58: Vom Hauptbahnhof fahren die Busse der Linie 19 ab 7 Uhr alle 8 Minuten ab. Die Busse der Linie 29 fahren alle 8 Minuten ab. Nach wie vielen Minuten fahren beide Linien gleichzeitig ab?
Alle Minuten fahren die Busse der beiden Linien gleichzeitig ab.
richtig: 0falsch: 0
Aufgabe 59: Ein undichter Wasserhahn tropft alle 40 Sekunden. Daneben befindet sich einer, der alle 45 Sekunden tropft. Nach wie vielen Sekunden tropfen beide gleichzeitig?

Nach jeweils Sekunden tropfen beide gleichzeitig.
Versuche: 0
Aufgabe 60: Das innere Zahnrad besteht aus 17 Zähnen und Vertiefungen, das äußere aus 36 Zähnen und Vertiefungen. Nach wie vielen Begegnungen von Zähnen und Zahnlücken treffen die gleichen Zähne und Lücken wieder aufeinander?
Ein abermaliges Zusammentreffen erfolgt nach Begegnungen.
Versuche: 0
Aufgabe 61: Trage jeweils das kleinste gemeinsame Vielfache der zwei Werte ein.
| a) = |
| b) = |
| c) = |
| d) = |
| e) = |
richtig: 0falsch: 0
Aufgabe 62: Trage jeweils das kleinste gemeinsame Vielfache der drei Werte ein.
| a) kgV(10, 18, 45) = |
| b) kgV(11, 20, 55)= |
| c) kgV(16, 24, 56) = |
| d) kgV(9, 28, 36) = |
| e) kgV(63, 70, 90) = |
Versuche: 0

