
von: Ernst Wallis et al (own scan)
Lizenz: Public Domain
Original: Hier
Satz des Thales
Thales von Milet war ein griechischer Wissenschaftler, Staatsmann und Ingenieur. Er lebte von ca. 624 v. Chr. bis 546 v. Chr. Nach ihm wird einer der bekanntesten Sätze der Mathematik benannt. Er beschreibt einen Zusammenhang, der aber bereits 2000 v. Chr. den Babyloniern bekannt war.
Aufgabe 1: Stelle den Satz des Thales zusammen.
Werden die von einem mit einem beliebigen auf der entsprechenden verbunden, erhält man immer ein Dreieck (90°).
Versuche: 0
Aufgabe 2: Bewege in der Grafik die orangen Punkte und stelle die Winkel α aus der Tabelle im Dreieck ein. Trage die dazugehörigen Winkel β und γ in die entsprechenden Textfelder ein.
| α | 40° | 43° | 48° | 50° | 55° | |||||
| β | ° | ° | ° | ° | ° | |||||
| γ | ° | ° | ° | ° | ° |
Versuche: 0
Aufgabe 3: Trage die Winkelsumme (α + β + γ) ein, die die in Aufgabe 2 gebildeten Dreiecke jeweils aufweisen.
Jedes Dreieck hat eine Winkelsumme von °.
Versuche: 0
Aufgabe 4: An welche Stelle der x-Achse muss der Punkt A gezogen werden, damit aus dem Dreieck ein rechtwinkliges Dreieck entsteht?.
Für ein rechtwinkliges Dreieck muss der Punkt A nach x = gezogen werden.
Versuche: 0
Aufgabe 5: Trage die fehlenden Winkel der jeweiligen Dreiecke ein.
| α | 0° | 1° | ° |
| β | ° | ° | 2° |
| γ | 90° | 90° | 90° |
richtig: 0falsch: 0
Aufgabe 6: Trage die gesuchten Winkel unten ein. Erinnere dich an den Satz des Thales in Aufgabe 1.
α = ° | β = °
richtig: 0falsch: 0
Aufgabe 7: Trage die gesuchten Winkel unten ein.
α = ° | β = °
richtig: 0falsch: 0
Aufgabe 8: Trage die gesuchten Winkel unten ein. Erinnere dich an den Satz des Thales in Aufgabe 1.
α = ° | β = ° | γ = °
richtig: 0falsch: 0
Aufgabe 9: Trage die gesuchten Winkel des gleichschenkligen Trapezes ein.
α = ° | β = °
richtig: 0falsch: 0
Aufgabe 10: Trage die gesuchten Winkel unten ein.
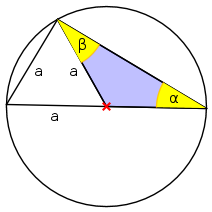
α = ° | β = °
Versuche: 0
Aufgabe 11: Trage die gesuchten Winkel unten ein.
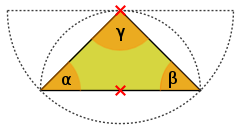
α = ° | β = ° | γ = °
Versuche: 0
Aufgabe 12: Trage die gesuchten Winkel unten ein.
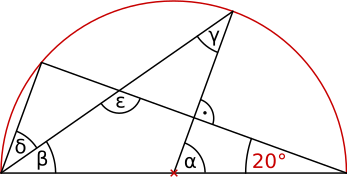
α = ° | β = ° | γ = ° | δ = ° | ε = °
Versuche: 0
|
Aufgabe 13: Wenn die Grundseite und die dazugehörige Höhe eines rechtwinkligen Dreiecks gegeben sind, lassen sie sich mit Hilfe des Thaleskreises sehr leicht konstruieren. Probiere es an der Grafik einfach einmal aus. |

