Erwartungswert
Der Erwartungswert E lässt sich mit Hilfe einer Tabelle berechnen. In diese werden die Werte W der Gewinne und ihre Wahrscheinlichkeiten P(W) eingetragen. Den Erwartungswert erhältst du, indem du die Werte mit den jeweiligen Wahrscheinlichkeiten multiplizierst und anschließend den Einsatz abziehst.
Beispiel: Ein Glücksrad hat die Farben rot, grün und blau. Der Einsatz für einmal drehen beträgt 2 €. Bei Rot werden 5 € und bei Grün 3 € ausgezahlt. Die blauen Felder sind ohne Gewinn. Wie groß ist der Erwartungswert?
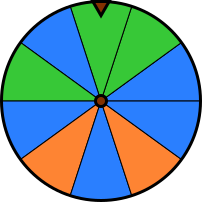 Gewinnplan: rot: 5 € grün: 3 € blau: 0 € |
rot | grün | blau | |
| W | 5 € | 3 € | 0 € | |
| P(W) | 2 10 | 3 10 | 5 10 | |
| W·P(W) | 5 € · 2 10 = 1 € | 3 € · 3 10 = 0,9 € | 0 € · 5 10 = 0 € | |
| E | (1 € + 0,9 € + 0 €) - 2 € = - 0,1 € | |||
Pro Einsatz macht der Spieler 0,10 € Verlust.
E < 0 (Verkäufer macht Gewinn) | E = 0 (faires Spiel) | E > 0 (Spieler macht Gewinn)
Aufgabe 1: Bei einer Tombola werden 200 Lose verkauft. Ein Los kostet 2 €. Es werden 72 Holzkreisel (je 0,50 €), 18 Frisbees (je 4 €), 9 USB-Sticks (je 6 €) und ein Einkaufsgutschein zu 30 € verlost. Wieviel Gewinn macht der Veranstalter durchschnittlich je Los? Trage die fehlenden Werte unten ein.
| Nieten | Holz- kreisel |
Fris- bees |
USB- Sticks |
Gut- schein |
- | Los- preis |
|
| W | 0 € | 0,5 € | 4 € | 6 € | 30 € | 2 € | |
| Anzahl | 100 | 72 | 18 | 9 | 1 | ||
| P(W) | 100 200 | 72 200 | 18 200 | 9 200 | 1 200 | ||
| W · P(W) | 0 € + | € | € | € | € | ||
| E | (0 € + ? € + ? € + ? € + ? €) | 2 € | |||||
Durchschnittlicher Veranstaltergewinn je Los: €
Versuche: 0
Aufgabe 2: Eine Kugel wird blind aus dem Glas gezogen. Die Zahlen geben den auszuzahlenden Geldbetrag in Euro an. Der Einsatz beträgt 2 Euro je Spiel. Trage die richtigen Werte ein. Welchen Gewinn macht der Spieler durchschnittlich?
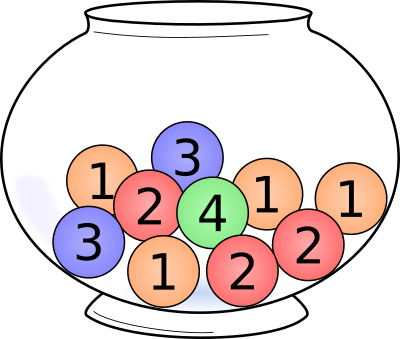
| Kugelwert | - | Ein- satz |
||||
| W | 1 € | 2 € | 3 € | 4 € | 2 € | |
| Anzahl | ||||||
| P(W) | 10 | 10 | 10 | 10 | ||
| W · P(W) | € | € | € | € | ||
| E | (? € + ? € + ? € + ? €) | 2 € | ||||
Durchschnittlicher Spielergewinn: €.
Versuche: 0
Aufgabe 3: Ein Losverkäufer nimmt 2 € pro Los. 80 % der Lose sind Nieten, bei 2 % der Lose gewinnst du 20 €, bei 5 bekommst du 10 €, bei 13 erhältst du 5 €. Berechnen den durchschnittlichen Gewinn, den der Losverkäufer auf lange Sicht pro Los macht!
| Gewinn | - | Los- preis |
||||
| W | 0 € | 5 € | 10 € | 20 € | 2 € | |
| P(W) | 80 % | |||||
| W · P(W) | 0 € | € | € | € | ||
| E | (0 € + ? € + ? € + ? €) | 2 € | ||||
Durchschnittlicher Gewinn des Verkäufers je Los: €
richtig: 0falsch: 0
Aufgabe 4: Für den Eintritt einer Party haben Gäste die Wahl. Sie können entweder 3 Euro zahlen oder mit einem sechsseitigen Würfel den Eintrittspreis werfen. Dann ist die erzielte Augenzahl in Euro zu begleichen. Wofür sollten sie sich entscheiden?
| Eintrittspreis | ||||||
 |
 |
 |
 |
 |
 |
|
| W | 1 € | 2 € | 3 € | 4 € | 5 € | 6 € |
| P(W) | 1 6 | 1 6 | 1 6 | 1 6 | 1 6 | 1 6 |
Die Gäste sollten sich für entscheiden. Dabei sparen sie durchschnittlich Cent.
Versuche: 0
Aufgabe 5: Ein fairer Würfel 
wird 15 Mal geworfen. Trage die Erwartungswerte für folgende Ereignisse ein.
| a) | Es wird gewürfelt. | E = |
| b) | Es wird gewürfelt. | E = |
| c) | Es wird gewürfelt. | E = |
richtig: 0falsch: 0
Aufgabe 6: Beim einem Dreh mit folgendem Glücksrad können 9 €, 4,5 € oder 3 € gewonnen werden, wenn das entsprechend gekennzeichnete Feld erreicht wird. Ein Spiel kostet 2,50 €. Wieviel Euro gewinnt der Veranstalter durchschnittlich je Spiel?
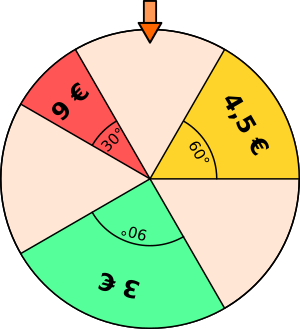
Durchschnittlicher Veranstaltergewinn je Spiel: €.
Versuche: 0
Aufgabe 7: In einem Beutel befinden sich 10 rote und 10 andersfarbige Kugeln. Bei diesem fairen Spiel wird eine Kugel gezogen. Der Spieleinsatz beträgt 2 Euro. Trage die richtigen Werte in die Tabelle ein.
| rot | blau | grün | |
| Anzahl | |||
| W | 1 € | 2,5 € | € |
| P(W) | % | % | 10 % |
Versuche: 0
Aufgabe 8: Du hast drei unterschiedlichen Münzspiele zur Auswahl. In jedem Spiel werden drei Würfe getätigt. Der Spieleinsatz beträgt immer ein Euro.
| Spiel A: | Du gewinnst 1,20 € wenn du höchstens 2x Zahl wirfst. |
| Spiel B: | Du gewinnst 2,00 € wenn du genau 2x Zahl wirfst. |
| Spiel C: | Du gewinnst 2,40 € wenn du mindestens 2x Zahl wirfst. |
Markiere die richtigen Pfade. Berechne für jedes Spiel den entsprechenden Erwartungswert (E) und trage ihn ohne Eurozeichen unten ein.
| A: höchstens 2x Zahl | ||||
| B: genau 2x Zahl | ||||
| C: mindestens 2x Zahl | ||||
 |
||||
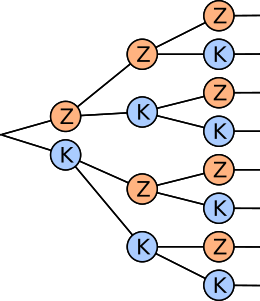| P(W) = |
0
8
|
0
8
|
0
8
|
| |
EA = | EB = | EC =
Versuche: 0
Aufgabe 9: Aus einer Box mit 12 roten und 20 blauen Kugeln werden zwei Kugeln gezogen und anschließend wieder zurückgelegt. Wie groß ist die durchschnittliche Anzahl gezogener blauer Kugeln?
20
20
20
20
20
20  |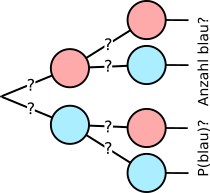
Durchschnittliche Anzahl blauer Kugeln:
richtig: 0falsch: 0