Kegel
Ein Kegel ist ein Körper, der über einer kreisförmigen oder elliptischen Grundfläche gebildet wird. Seine gleichmäßig gekrümmte Mantelfläche läuft auf eine Spitze zu.
Berechnung des Volumens (V)
Das Kegelvolumen hat 3-mal Platz im Volumen eines Zylinders mit gleichem Radius und gleicher Höhe. Um das Kegelvolumen (V) zu berechnen, wird die Volumenformel des Zylinders "Grundfläche (G) · Höhe (h)" durch drei geteilt.
| V = | G · h |
| 3 |
| V = | π · r² · h |
| 3 |
Berechnung der Oberfläche (O)
Zur Oberfläche eines Kegels gehört die Grundfläche (Kreis) und die Mantelfläche (Kreisausschnitt). Die Formel für die Grundfläche lautet: G = π · r². Der Bogen des Kreisausschnitts ist so lang wie der Umfang des Grundflächekreises (π · 2r). Durch geschicktes Zerteilen lässt sich aus der Mantelfläche ein Rechteck bilden, dessen eine Seitenlänge so groß ist wie die Seitenlänge (s) des Kreisausschnitts und dessen andere Länge so groß ist wie die Hälfte des Grundflächenumfangs (π · r). Die Formel für die Mantelfläche lautet daher: M = π · r · s. Zur Bestimmung der Oberfläche werden Grundfläche und Mantelfläche addiert.
O = π · r² + π · r · s
Aufgabe 1: Bewege die orangen Gleiter der Grafik und beobachte, wie sich Kegelnetz und Kegel verändern.
Aufgabe 2: Ziehe die Ergebnisse ins richtige Feld.
Formeln:
|
Versuche: 0
Aufgabe 3: Trage die richtige Oberfläche und das richtige Volumen des Kegels unten ein.
|
|
|
a) Volumen = cm³
richtig: 0 | falsch: 0
|
|
b) Oberfläche = cm²
richtig: 0 | falsch: 0
|
Volumen
Aufgabe 4: Berechne das Volumen des folgenden Körpers. Trage den fehlenden ganzzahligen Wert ein.
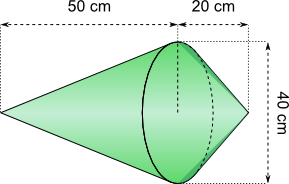
Der Körper hat ein Volumen von ,53 cm³
Versuche: 0
Aufgabe 5: Der folgende Körper besteht aus zwei Kegeln. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 6: Trage das Volumen des folgenden Körpers ein. Runde auf ganze cm³.
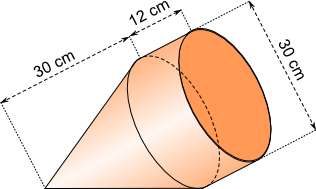
Der Körper hat ein Volumen von cm³.
Versuche: 0
Aufgabe 7: Der folgende Körper besteht aus einem Kegel und einem Zylinder. Trage das Volumen ein. Runde auf eine Nachkommastelle.
Der Körper hat ein Volumen von cm³.
richtig: 0falsch: 0
Aufgabe 8: Stelle die Rechnung für das Volumen des folgenden Körpers auf. Berechne zuerst das Volumen des Zylinders (VZ). Ziehe dann das Kegelvolumen (VK) ab und berechne das Ergebnis. Anschließend multipliziere VZ mit 2 3 und trage das Ergebnis an entsprechender Stelle ein. Runde immer auf ganze Kubikzentimeter.
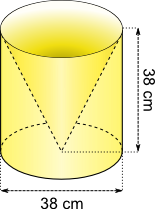 |
Rechnung:
|
Versuche: 0
Aufgabe 9: Die Flächen drehen sich um die rote Achse, so dass Drehkörper entstehen. Trage den ganzzahligen Wert des Volumens der drei Drehkörper ein.
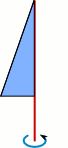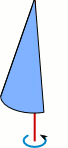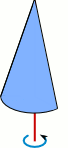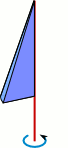
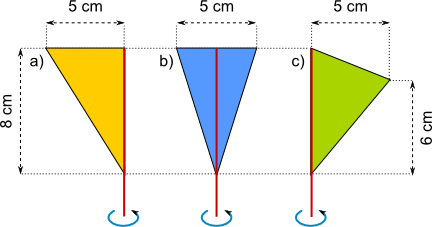
Va = ,4 cm³; Vb = ,4 cm³; Vc = ,4 cm³
Versuche: 0
Aufgabe 10: Ein Kegel mit einem Volumen von hat einen Radius von . Gib die Höhe des Kegels an. Runde auf ganze cm.
Der Kegel hat eine Höhe von cm.
richtig: 0falsch: 0
Aufgabe 11: Drei Kegel haben die gleiche Grundfläche. Der nächst kleinere Kegel wird jeweils in der Höhe halbiert. Berechne das je dazugehörige Volumen. Runde auf eine Nachkommastelle.
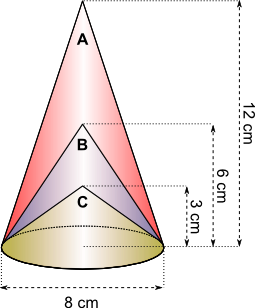
Antwort: VA = cm³; VB = cm³; VC = cm³
Versuche: 0
Fällt dir etwas am Verhältnis zwischen den Volumina und den Höhen der Kegel auf?
Aufgabe 12: Trage unten in die Gleichung einen Radius und eine Kegelhöhe so ein, dass das Kegelvolumen zwischen und cm³ liegt.
| G |
· | h | : 3 = | V |
| π · ² cm² | · | cm | : 3 = | cm³ |
richtig: 0 | falsch: 0
Aufgabe 13 Ein 80 cm hoher Kegel steht auf einem 80 cm hohen Quader, dessen rechteckige Grundfläche 136 cm lang und 102 cm breit ist. Die Kreislinie der Kegelgrundfläche streift alle vier Ecken der Quadergrundfläche. Wie viel Kubikmeter (m³) Volumen hat dieser zusammengesetzte Körper? Runde auf eine Stelle nach dem Komma.
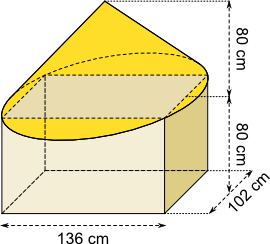
Kegel und Quader haben zusammen ein Volumen von m³.
Versuche: 0
Oberfläche
Aufgabe 14: Trage die Oberfläche des folgenden Körpers ein. Runde auf ganze Quadratzentimeter
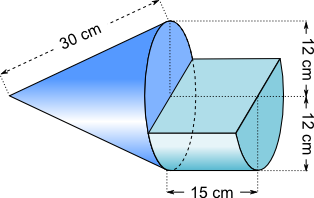
Der Körper hat eine Oberfläche von cm².
Versuche: 0
Aufgabe 15: Trage die Oberfläche des folgenden Körpers ein. Runde auf ganze Quadratzentimeter
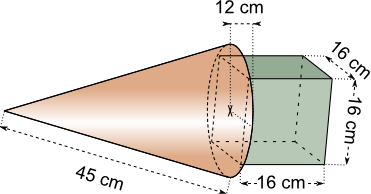
Der Körper hat eine Oberfläche von cm².
Versuche: 0
Aufgabe 16: Trage die Oberfläche des folgenden Körpers ein. Runde auf ganze Quadratzentimeter
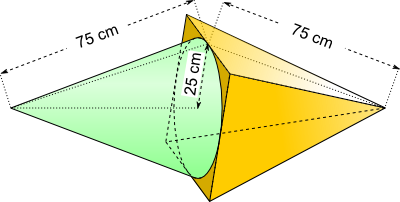
Der Körper hat eine Oberfläche von cm².
Versuche: 0
Aufgabe 17: Trage die fehlenden ganzzahligen Werte ein. (Die aufgeführten Kommastellen sind gerundet.)
| Radius r | ,0 cm | ||
| Seitenlinie s | ,0 cm | ,0 cm | |
| Mantelfläche M | |||
| Oberfläche O |
richtig: 0falsch 0
Aufgabe 18: Trage unten in die Gleichung einen Radius und eine Länge der Seitenlinie so ein, dass die Mantelfläche zwischen und cm² liegt.
| π · | r |
· | s | = | M |
| π · | cm | · | cm | = | cm² |
richtig: 0 | falsch: 0
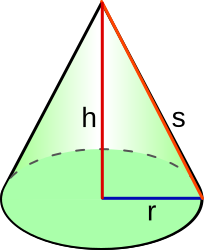
Satz des Pythagoras
Aufgabe 19: Klick das richtige Volumen des grünen Kegels an. Berechne die fehlenden Streckenlänge mit dem Satz des Pythagoras. Achte auf die Einheiten.
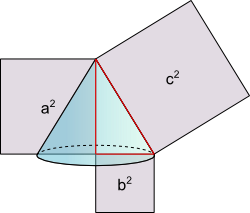
Maße in cm |
|
|
Volumen = dm³
richtig: 0 | falsch: 0 |
|
Aufgabe 20: Klicke die richtige Oberfläche des gelben Kegels an. Berechne die Länge der Seitenlinie mit dem Satz des Pythagoras. Achte auf die Einheiten.

Maße in cm |
|
Oberfläche = dm²
richtig: 0 | falsch: 0 |
Aufgabe 21: Berechne mithilfe des Satzes von Pythagoras die gesuchte Größe.
| a) |
r = 20 cm h = 21 cm s = cm |
b) |
r = 33 cm h = 56 cm s = cm |
c) |
r = 39 m h = m s = 89 m |
d) |
r = m h = 55 m s = 73 m |
Versuche: 0
Aufgabe 22: Trage die fehlenden ganzzahligen Werte ein. (Die aufgeführten Kommastellen sind gerundet.)
| Radius r | cm | dm | m | m |
| Kegelhöhe h | cm | dm | m | m |
| Seitenlinie s | cm | dm | m | m |
| Volumen V | cm³ | dm³ | m³ | m³ |
richtig: 0falsch 0
Aufgabe 23: Trage die fehlenden ganzzahligen Werte ein. (Die aufgeführten Kommastellen sind gerundet.)

| Radius r | ,0 cm | ||
| Pyramidenhöhe h | ,0 cm | ,0 cm | |
| Mantelfläche M | |||
| Oberfläche O |
richtig: 0falsch 0
Aufgabe 24: Aus dem Kegel wurde ein Stück herausgeschnitten. Gegeben sind die Längen AS = 48,1 cm und MS = 36 cm Um wie viel Prozent hat sich die Oberfläche des Körpers verringert? Runde auf ganze Prozent. Achtung: Die rot gefärbten Flächen sind neu entstanden.
Die Körperoberfläche hat sich um % verringert.
Versuche: 0
Aufgabe 25: Ein hoher kegelförmiger Sandhaufen hat einen Durchmesser von . Wie viel m³ Sand wurden angehäuft? Trage den fehlenden ganzzahligen Wert ein.
Der Haufen besteht aus , Sand.
richtig: 0falsch: 0
Aufgabe 26: Der Aushub einer Baugrube wurde vom Bagger zu einem 3 Meter hohen kegelförmigen Hügel aufgeschüttet. Er hat einen Durchmesser von 9 Metern. Die Erde wiegt 1,7 t/m³. Ein LKW kann je Fuhre eine Zuladung von 3,5 t abfahren. Nach wie vielen LKW-Fahrten kann der komplette Aushub frühestens abtransportiert sein?
Wenn die LKWs nicht überladen werden, sind mindestens Fahrten nötig, um den gesamten Aushub fortzuschaffen.
Versuche: 0
Aufgabe 27: Ein gusseiserner Kegel hat einen Radius von 7 cm und eine Höhe von 28 cm. Trage den ganzzahligen Wert des Gewichts ein. 1cm³ Eisen wiegt 7,5 g.
Der Kegel wiegt , kg.
richtig: 0falsch: 0
Aufgabe 28: Trage den ganzzahligen Wert des Gewichts des Aluminiumkörpers (Dichte: 2,7 g/cm³) ein.
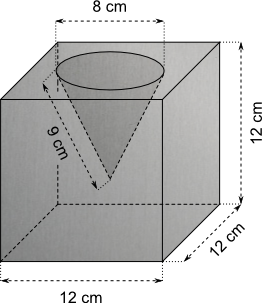
Der Körper wiegt ,9 g
Versuche: 0
Aufgabe 29: Ein kegelförmiger Messbecher hat eine Höhe von 13 cm und oben einen inneren Durchmesser von 13,6 cm.
| a) | Wie viel cm³ Wasser passen in den Messbecher? | 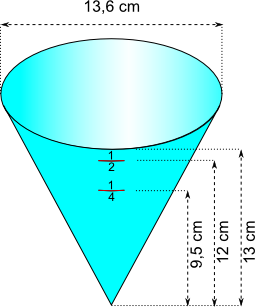 |
| b) | Die Markierung für 0,5 Liter liegt in 12 cm Höhe? Wie groß ist hier der Innenradius des Messbechers? | |
| c) | Die Markierung für ¼ Liter liegt in einer Höhe von 9,5 cm. Wie viel cm sind es von hier bis zum äußeren oberen Rand des Messbechers entlang der Mantellinie? | |
Antwort: |
Runde jeweils auf eine Stelle nach dem Komma. |
|
| a) | Der Messbecher fasst cm³ Wasser. | |
| b) | Der Innenradius an der 0,5-Liter-Marke beträgt cm. | |
| c) | Die Strecke ist cm lang. | |
Versuche: 0
Aufgabe 30: Ein kegelförmiges Spitzdach soll neu gedeckt werden. Es hat eine Höhe von 8 m und einen Durchmesser von 7,80 m. Wie viel Quadratmeter Dachfläche sind mit Ziegeln zu bedecken? Runde auf ganze m².
Das Spitzdach hat eine Fläche von m².
Versuche: 0
Aufgabe 31: Trage das Volumen des folgenden Zeltes in Kubikmeter ein. Runde auf eine Stelle nach dem Komma. Achte auf die Einheiten.
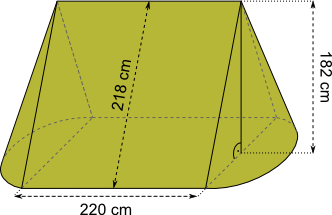
Das Zelt hat ein Volumen von m³.
Versuche: 0