Quadratische Funktion
Aufgabe 1: Trage die richtigen Begriffe ein.
- Quadratische Funktionen haben eine quadrierte Variable (x²).
- Die einfachste (tschiraquade) Funktion hat die Gleichung y = x².
- Ihr Graph heißt (paraNormablle).
- Die Normalparabel verläuft symmetrisch zu der Achse, durch die das (Minumim) verläuft.
- Sie ist nach (bone) hin geöffnet.
- Den tiefsten Punkt der Parabel nennt man (eitelSchpunkt).
Versuche: 0
Normalparabel (y = x²)
Aufgabe 2: Bewege den orangen Gleiter der Parabel auf die aufgeführten x-Punkte der Parabel. Trage die entsprechenden y-Werte in die Tabelle ein.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x² |
Versuche: 0
Aufgabe 3: Trage die richtigen y-Werte in die Tabelle ein.
| x | -6 | -5 | -4 | ··· | 4 | 5 | 6 |
| y = x² | ··· |
Versuche: 0
Aufgabe 4: Berechne die fehlenden Koordinaten der Normalparabel und trage sie ein.
| A( | ); B( | ); C( | | | ); D( | | | ) | ||||
richtig: 0falsch: 0
Parabelform y = ax²
Veränderte Parabelöffnung - Streckfaktor
Aufgabe 5: Ziehe den Regler der Grafik und beobachte die Veränderungen der Parabel. Klick anschließend die richtigen Begriffe an.
Merke dir bitte:
Multiplizert man x² mit einem Faktor (a), dann verändert sich die Öffnung der Parabel.
Versuche: 0 |
Aufgabe 6: Ergänze die Funktionsgleichungen so, dass sie zu den dazugehörigen Aussagen passen.
|
a) Die Parabelöffnung zeigt nach oben: y = x². b) Die Parabelöffnung zeigt nach unten: y = x². c) Die Parabel ist schmaler als die Normalparabel: y = x². d) Die Parabel ist breiter als die Normalparabel: y = x². |
richtig: 0 | falsch: 0
Aufgabe 7: Ergänze die Funktionsgleichungen so, dass sie zu den dazugehörigen Aussagen passen.
|
a) Parabelöffnung oben und schmaler als die Normalparabel: y = x². b) Parabelöffnung oben und breiter als die Normalparabel: y = x². c) Parabelöffnung unten und schmaler als die Normalparabel: y = x². d) Parabelöffnung unten und breiter als die Normalparabel: y = x². |
richtig: 0 | falsch: 0
Aufgabe 8: Klick die richtigen Funktionsgleichungen an.
|
a)
|
b)
|
||||||||||||||||||||||||
|
c)
|
d)
|
Versuche: 0
Aufgabe 9: Ordne den Funktionsgleichungen die richtigen Parabeln zu.
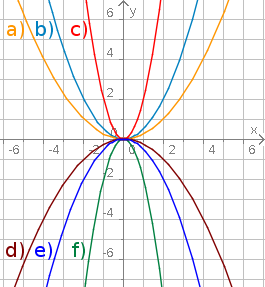 |
Bestimmung einer Funktionsgleichung
Mit den Koordinaten eines Punktes, der auf einer Parabel der Form y = ax2 liegt, lässt sich der Faktor a berechnen. Dafür werden die Koordinaten in die Formel eingesetzt, die dann nach a hin aufgelöst wird.
| Beispiel: | ||||
P(3,18) liegt auf der Parabel |
y = ax2 | |||
| • Koordinaten einsetzen | 18 = a · 32 | |||
| • Nach a hin auflösen |
|
|||
| a = 2 | ||||
| • Funktionsgleichung: | y = 2x2 | |||
Aufgabe 10: Die Parabel einer quadratischen Funktion der Form y = ax2 führt durch den Punkt P( ). Trage den Faktor der Funktion unten ein.
Funktionsgleichung: y = x 2
richtig: 0falsch: 0
Aufgabe 11: Eine 6 Meter hohe Brücke hat einen parabelförmigen Bogen. Ihre Spannweite beträgt 40 Meter. Trage den Faktor a in die Funktion ein.
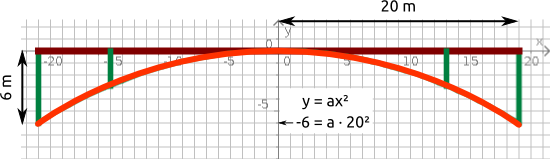
Antwort: Die zum Bogen gehörende Funktionsgleichung lautet: y = x².
Versuche: 0
Parabelform y = ax² + c
Vertikale Parabelverschiebung
Aufgabe 12: Ziehe den Regler c der Grafik und beobachte die Veränderungen der Parabel. Klick anschließend die richtigen Begriffe an.
|
Merke dir bitte:
Eine Parabel der Form ax² + c ist in vertikaler Richtung verschoben.
Versuche: 0 |
Aufgabe 13: Ziehe die Begriffe an die richtige Stelle.
| Verglichen mit der Normalparabel | ||
| ist die Öffnung dieser Parabel ... (breiter | schmaler) | befindet sich diese Parabel weiter ... (oben | unten) | |
| a) y = -½x² + 2,5 | ||
| b) y = 4x² - 1,5 | ||
| c) y = -½x² - 3 | ||
| d) y = -3x²+ 1,5 | ||
| e) y = -3x² - 2 | ||
| f) y = ¾x² + 3 | ||
| g) y = 4x² + 2 | ||
| h) y = ¾x² - 2,5 | ||
Versuche: 0
Aufgabe 14: Ergänze die Funktionsgleichungen so, dass sie zu den Parabeln passen.
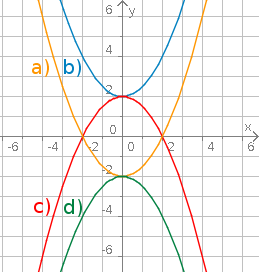
| a) y = | b) y = | |
| c) y = | d) y = |
Versuche: 0
Aufgabe 15: Berechne y und trage es ein.
| a) |
Formel x = 0 y = |
b) |
Formel x = 0 y = |
c) |
Formel x = 0 y = |
| d) |
Formel x = 0 y = |
e) |
Formel x = 0 y = |
f) |
Formel x = 0 y = |
richtig: 0falsch: 0
Nullstellen der Funktion y = ax² + c
Parabelschnittpunkte mit der x-Achse
Die Nullstellen der Funktion befinden sich dort, wo die Parabel die x-Achse schneidet. An diesen Stellen ist der y-Wert Null.
Aufgabe 16: Bewege die beiden Gleiter der Grafik und beobachte, in welchem Verhältnis a und c sich zueinander befinden müssen, damit die Parabel die Nullstelle (y = 0) schneidet. Ordne anschließend die folgenden Aussagen richtig zu.
Aufgabe 17: Stelle in der Grafik der vorherigen Aufgabe die folgenden Funktionen ein. Lies die entsprechenden Nullstellen ab und trage die Werte ohne Vorzeichen ein.
| a) | y = x² - 1 y = 0 x1 = ; x2 = - |
b) | y = 0,4x² - 3,6 y = 0 x1 = ; x2 = - |
c) | y = ½x² - 2 y = 0 x1 = ; x2 = - |
| d) | y = -3x² + 3 y = 0 x1 = ; x2 = - |
e) | y = 4x² - 1 y = 0 x1 = ; x2 = - |
f) | y = -0,1x² + 2,5 y = 0 x1 = ; x2 = - |
Versuche: 0
Aufgabe 18: Trage unten die Nullstellen der Funktion ein.
y = x2 - 3
x1 = | x2 = -
richtig: 0falsch: 0
Aufgabe 19: Ordne zu, ob die Parabeln unten keine, eine oder zwei Nullstellen haben.
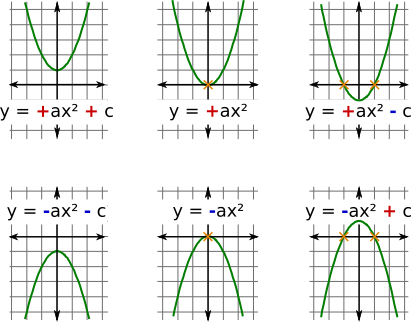
| a) | b) |
Parabelform y = a(x + b)² + c
Vertikale und horizontale Parabelverschiebung
Aufgabe 20: Ziehe den Regler b der Grafik und beobachte die Veränderungen der Parabel. Klick anschließend die fehlenden Begriffe an.
|
Merke dir bitte:
Bei einer Parabel der Form a(x + b)² + c beeinflusst b die horizontale Ausrichtung des Graphen.
Versuche: 0 |
Aufgabe 21: Trage den Scheitelpunkt der Parabeln ein.
| a) y = | Sa(|) |
| b) y = | Sb(|) |
| c) y = | Sc(|) |
| d) y = | Sd(|) |
richtig: 0falsch: 0
Aufgabe 22: Vervollständige die Funktionsgleichungen der verschobenen Normalparabeln.
| a) y = (x )² | Sa() |
| b) y = (x )² | Sb() |
| c) y = (x )² | Sc() |
| d) y = (x )² | Sd() |
richtig: 0falsch: 0
Aufgabe 23: Ordne die Begriffe richtig zu.
- Ist der Streckfaktor a positiv, dann zeigt die Parabelöffnung nach .
- Ist der Streckfaktor a negativ, dann zeigt die Parabelöffnung nach .
- Ist der Abstand zum Nullpunkt (Betrag) von a größer als 1, dann ist die Parabel als die Normalparabel.
- Ist der Abstand zum Nullpunkt (Betrag) von a kleiner als 1, dann ist die Parabel als die Normalparabel.
- Ist b positiv, verschiebt sich die Parabel nach .
- Ist b negativ, verschiebt sich die Parabel nach .
- Ist c positiv, verschiebt sich die Parabel nach .
- Ist c negativ, verschiebt sich die Parabel nach .
Versuche: 0
Aufgabe 24: Ordne den Funktionsgleichungen die richtigen Parabeln zu.
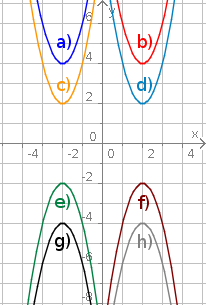 |
Aufgabe 25: Die abgebildete Parabel wird gespiegelt. Trage die Funktionsgleichungen der gespiegelten Parabeln ein.
| Funktion: |
|
| a) | Spiegelung an der x-Achse: Funktion: y = (x)2 |
| b) | Spiegelung an der y-Achse: Funktion: y = (x)2 |
| c) | Spiegelung an x- und y-Achse: Funktion: y = (x)2 |
richtig: 0falsch: 0
Aufgabe 26: Die abgebildete Parabel wird an den farbigen Achsen gespiegelt. Trage die Funktionsgleichungen der gespiegelten Parabeln ein.
| Funktion: |
|
| a) | Spiegelung an blauer Achse: Funktion: y = (x)2 |
| b) | Spiegelung an grüner Achse: Funktion: y = (x)2 |
| c) | Spiegelung an blauer und grüner Achse: Funktion: y = (x)2 |
richtig: 0falsch: 0
Aufgabe 27: Die Gleichung einer Parabel (y = a(x + b)2 + c) mit dem Scheitel S() geht durch den Punkt P(). Bestimme den Streckfaktor a.
a =
richtig: 0falsch: 0
Aufgabe 28: Wandle den Term in die Scheitelpunktform um und gib die Koordinaten des Scheitelpunktes an.
y = x2 - 6x + 10
y = x2 - 2 · x + 10
y = x2 - 2 · x + +
y = (x - )2 +
S(|)
richtig: 0falsch: 0
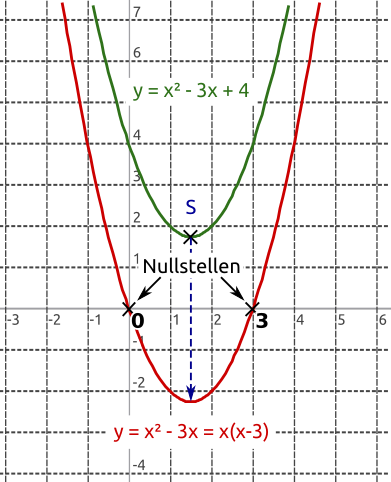
Aus der allgemeinen Form einer Parabel kann der Scheitelpunkt nicht abgelesen werden. Um das zu ermöglichen, kann man auch folgendermaßen vorgehen:
Gegeben ist die grüne Parabel y = x2 - 3x + 4. Sie wird um - 4 in y-Richtung verschoben, um durch den Ursprung zu laufen. Der Scheitelpunkt der neuen (roten) Parabel y = x2 - 3x und der Scheitelpunkt der grünen Parabel verlaufen durch die gleiche x-Koordinate. Um die Nullstellen der roten Parabel rechnerisch zu bestimmen, klammert man aus: y = x2 - 3x = x · (x - 3). Das Ergebnis einer Multiplikation ist null, wenn einer der Faktoren null ist. Die Nullstellen der roten Parabel befinden sich demnach auf x = 0 und (x - 3) = 0 also x = 3. Die x-Koordinate des Scheitelpunktes der roten Parabel befindet sich in der Mitte der beiden Nullpunkte, also bei (0 + 3) : 2 = 1,5. Somit liegt auch die x-Koordinate des Scheitelpunktes der grünen Parabel bei 1,5. Um die y-Koordinate des Scheitelpunktes der grünen Parabel zu ermitteln, wird jetzt der Wert der x-Koordinate in die entsprechende Formel eingesetzt und die Gleichung berechnet: y = 1,52 - 3 · 1,5 + 4 = 1,75. Der Scheitelpunkt der grünen Parabel liegt bei S(1,5|1,75).
Aufgabe 29: Berechne die Koordinaten des Scheitelpunktes der folgenden Funktion nach dem oben angegebenen Muster.
Funktion:
S(|)
richtig: 0falsch: 0
Funktionsgleichung einer Normalparabel aus zwei Punkten bestimmen.
Sind zwei Punkte einer Parabel der Form y = x² + ax + c bekannt, lässt sich Funktionsgleichung folgendermaßen erschließen.
- Die Koordinaten der beiden Punkte in die Normalform einsetzen
- Berechnen von a und c mithilfe eines linearen Gleichungssystems »
- Funktionsgleichung ermitteln
Die Punkte P(-6|11) und Q(2|3) liegen auf einer verschobenen Normalparabel.
| P(-6|11) | (I) | 11 | = | (-6)2 + a · (-6) + c | ||
| Q(2|3) | (II) | 3 | = | 22 + a · 2 + c | | · (-1) | |
| (I') | 11 | = | 36 - 6a + c | |||
| (II') | -3 | = | -4 - 2a - c | |||
| (I' + II') | 8 | = | 32 - 8a | | - 32 | ||
| -24 | = | -8a | | : (-8) | |||
| 3 | = | a | ||||
| (a in II) | 3 | = | 22 + 3 · 2 + c | |||
| 3 | = | 10 + c | | - 10 | |||
| -7 | = | c | ||||
| Funktionsgleichung: | y | = | x2 + 3x - 7 | |||
Aufgabe 30: Die Punkte P(|) und Q(|) liegen auf einer verschobenen Normalparabel. Trage unten die fehlenden Werte der dazugehörigen Funktionsgleichung ein.
y = x2 x
richtig: 0falsch: 0
Aufgabe 31: Die Punkte A(-3|19) und B(3|7) liegen gleichzeitig auf der verschobenen Normalparabel f und der Geraden g ». Trage die fehlenden Größen der beiden Funktionsgleichungen unten ein.
f) y = x2 x | g) y = x
Versuche: 0
Aufgabe 32: Trage unten die maximale Flughöhe des Skateboards ein.
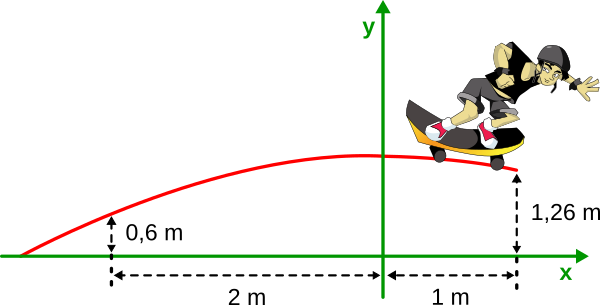
Die maximale Flughöhe beträgt m.
Versuche: 0

