Quader 
Ein Quader ist ein Körper, der aus drei Rechteckpaaren gebildet wird. Je zwei gegenüberliegende Rechtecke sind gleich groß. Seine Kanten stehen an den Ecken senkrecht aufeinander. Er hat 6 Flächen, 8 Ecken und 12 Kanten. Der Würfel ist ein spezieller Quader. Bei ihm sind alle Kanten gleich lang.
Anmerkung: Volumen und Oberflächeninhalt von Prisma und Zylinder werden faktisch nach gleichem Schema berechnet. Im Film wird in didaktischer Vereinfachung der Zylinder als Spezialfall eines Prismas mit unendlich vielen Ecken eingeordnet. Streng mathematisch gesehen ist ein Zylinder aber kein Prisma, da die Grundfläche eines Zylinders kein Polygon mit unendlich vielen Ecken sondern ein Kreis ohne Ecken ist.
Berechnung des Volumens (V)
Das Quadervolumen wird mit Grundfläche mal Höhe berechnet (V = G · h). Bei einem Quader kann jede Fläche die Grundfläche sein. Typische Volumenberechnungen mit Hilfe der Kantenlängen lauten:
Quader: V = a · b · c
Würfel: V = a · a · a oder V = a³
Oberfläche (O)
Die Oberfläche eines Quaders besteht aus den Rechtecken der Grund-, der Deck- und der Mantelfläche. Grund- und Deckfläche sind gleich groß und werden mit Länge (a) mal Breite (b) berechnet (G = a · b). Da die Mantelflächen alle die gleiche Höhe (h) besitzen, kann der Umfang der Grundfläche (2a + 2b) mit der Höhe (h) multipliziert werden, um den Flächeninhalt der gesamten Mantelfläche zu berechnen. M = (2a + 2b) · h. Es kann aber auch jedes Rechteck der Mantelfläche einzeln berechnet und danach die Summe aller Mantelrechtecke gebildet werden. M = a · h + b · h + a · h + b · h.
O = 2(a · b) + (2a + 2b) · h
Aufgabe 1: Ziehe an den orangen Gleitern der Grafik und beobachte, wie sich der Quader und das Quadernetz verändern.
Aufgabe 2: Klick die richtigen Terme an.
Formeln:
|
Versuche: 0
Aufgabe 3: Der Käfer "besucht" jede der 8 Ecken des Quaders ein einziges Mal und nimmt dabei die rot gekennzeichnete Strecke. Wie viel Zentimeter Weg hat er dabei zurückgelegt?
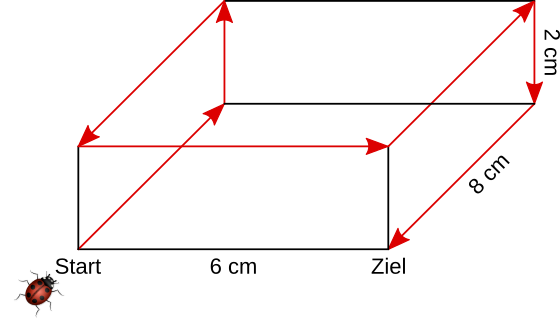
Sein Weg hat eine Länge von cm.
Versuche: 0
Aufgabe 4: Zehn kleine Würfel passen in jeder Körperrichtung in den großen blauen Würfel hinein. Klick unten an, in welchen großen Würfel die angegebene Menge kleiner Würfel insgesamt hineinpasst.
|
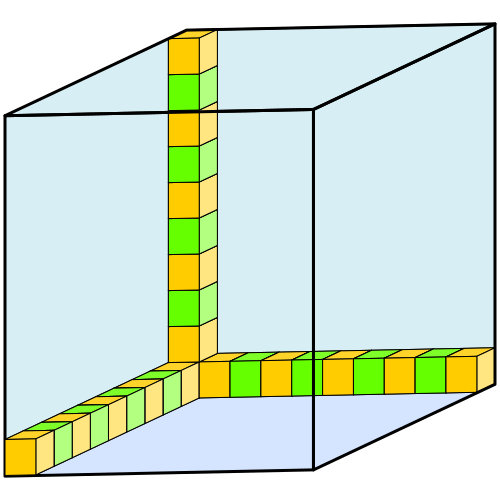
Versuche: 0
Aufgabe 5: Trage das Volumen und die Oberfläche des Quaders unten in das Textfeld ein. Eine Auswertung findet während der Eingabe statt.
|
a) Volumen: cm3
|
b) Oberfläche: cm2
|
Aufgabe 6: Gib an, wie groß das Volumen des Quaders aus Aufgabe 5 ist , wenn ...
| a) Länge und Tiefe gleich bleiben, sich die Höhe aber verdoppelt. | Antwort: cm³ |
| b) die Länge gleich bleibt und sich die Tiefe und die Höhe verdoppelt. | Antwort: cm³ |
| c) alle drei Kantenlängen sich verdoppeln. | Antwort: cm³ |
Versuche: 0
Aufgabe 7: Trage Volumen und Oberfläche der Quader ein.
| Länge a | cm | dm | m |
| Breite b | cm | dm | m |
| Höhe h | cm | dm | m |
| Volumen V | cm³ | dm³ | m³ |
| Oberfläche O | cm² | dm² | m² |
richtig: 0falsch: 0
Aufgabe 8: Trage die gesuchten Werte ein. Berechne das Gewicht auf 3 Stellen nach dem Komma genau.
| Länge a | cm | cm | cm | cm |
| Breite b | cm | cm | cm | cm |
| Höhe h | cm | cm | cm | cm |
| Volumen V | cm³ | cm³ | cm³ | cm³ |
| Gewicht je cm³ | g | g | g | g |
| Gewicht | kg | kg | kg | kg |
richtig: 0falsch 0
Aufgabe 9: Trage die fehlenden Größen der Quader ein.
| Länge a | cm | cm | m | m |
| Breite b | cm | cm | m | m |
| Höhe h | cm | cm | m | m |
| Volumen V | cm³ | cm³ | m³ | m³ |
| Oberfläche O | cm² | cm² | m² | m² |
richtig: 0falsch 0
Aufgabe 10: Ziehe die orangen Punkte so, dass 2 Quadernetze entstehen. Wenn die Netze richtig konstruiert sind, färben sie sich blau.
Aufgabe 11: Ein Würfel mit einer Kantenlänge von 7 cm wird in zwei gleich große Quader zerlegt.
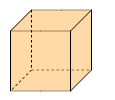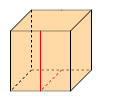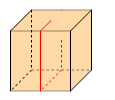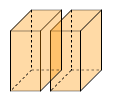a) Trage Volumen und Oberfläche des Würfels unten ein.
b) Trage Volumen und Oberfläche von einem der Quader unten ein.
b) VQuader = cm³; OQuader = cm²
Versuche: 0
Aufgabe 12: Ein 2,40 m langer Balken mit quadratischem Querschnitt (20 cm x 20 cm) wird in der Höhe und in der Breite halbiert. Anschließend werden die ausgesägten Teile so zersägt, dass Würfel entstehen. Wie viele Würfel erhält man aus diesem Balken?
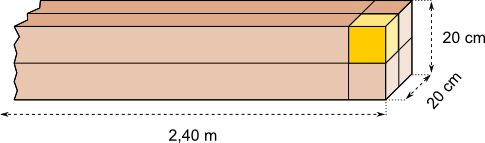
Aus dem Balken lassen sich Würfel heraussägen.
Versuche: 0
Aufgabe 13: Zwei Würfel mit einer Kantenlänge von 4 cm werden zu einem Quader zusammengefügt. Trage Volumen und Oberfläche des Quaders ein.
Der Quader hat ein Volumen von cm³ und eine Oberfläche von cm².
Versuche: 0
Aufgabe 14: Die Kanten des gelben Würfels sind doppelt so lang wie die Kanten des blauen Würfels. Wie viel mal größer ist das Volumen und die Oberfläche des gelben Würfels?
b) Die Oberfläche des gelben Würfels ist mal so groß wie die Oberfläche des blauen Würfels.
Versuche: 0
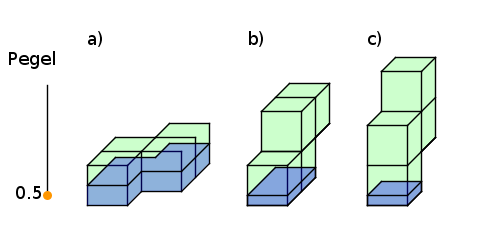
Aufgabe 15: Das "Würfelaquarium" a ist zur Hälfte mit Wasser gefüllt. Bis zu welchem Pegel steigt die gleiche Menge Wasser in Aquarium b und c? Du kannst den Pegel mit den Pfeiltasten einstellen.
| © 2000 - http://geonext.de | |||||
 |
|||||
|
|
a) Der Wasserpegel steigt in Aquarim b bei gleicher Wassermenge bis zu Pegel
.
b) Der Wasserpegel steigt in Aquarim c bei gleicher Wassermenge bis zu Pegel . |
Versuche: 0
Aufgabe 16: Ein würfelförmiger Wasserbehälter steht gekippt im Garten.
| a) | Wie viel Liter Wasser befindet sich im Auffangbecken? |
| b) | Wie hoch steht das Wasser, wenn der Behälter horizontal gestellt wird? |
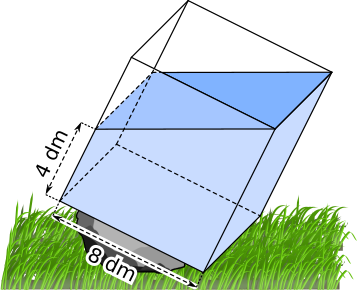
| a) | Im Becken sind Liter Wasser. |
| b) | Im horizontal aufgestellten Behälter steht das Wasser dm hoch. |
Versuche: 0
Aufgabe 17: In einem Wasserbehälter mit 12 m² Grundfläche steht das Wasser 6 m hoch. Es werden 30 m³ Wasser abgelassen. Wie hoch steht das Wasser in diesem Behälter jetzt?
Das Wasser hat nun eine Höhe von Metern.
Versuche: 0
Aufgabe 18: Ein bis zum Rand gefüllter quaderförmiger Wasserbehälter wird gekippt. Trage unten ein, wie viel Liter Wasser sich in den jeweiligen Schräglagen im Behälter befindet.
a) |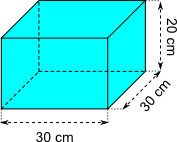
b) |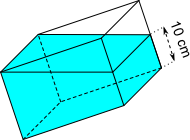
c) |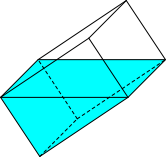
| Liter | Liter | Liter |
Versuche: 0
Aufgabe 19: In einer Fabrik werden Getränkepackungen mit folgender Bodengröße hergestellt. Die Verpackungen haben einen Rauminhalt von exakt einem Liter. Trage die genaue Höhe der jeweiligen Verpackung ein.
| 10 cm | a) | b) | c) | d) | |||
| 5 cm | 8 cm | 10 cm | 12,5 cm | ||||
| Höhe: | cm | cm | cm | cm |
Versuche: 0
Aufgabe 20: Trage das Volumen des folgenden Körpers unten ein.
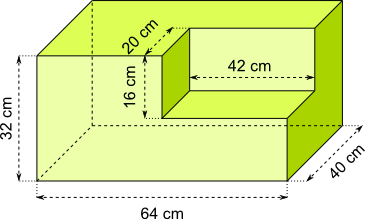
Der Körper hat ein Volumen von cm³.
Versuche: 0
Aufgabe 21: Trage das Volumen der folgenden Körper unten ein.
 |
 |
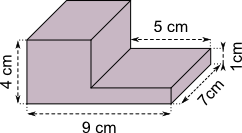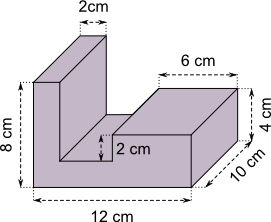| V = cm³ | V = cm³ |
Versuche: 0
Aufgabe 22: Ein aus 1 cm dickem Sperrholz gebastelter Papierkorb steht auf einer 30 cm x 30 cm breiten Grundplatte und ist 50 cm hoch. Jule will die Seitenwände innen und außen sowie den Boden innen mit Folie bekleben. Die oberen Stirnseiten der Bretter und die Unterseite des Bodens bleiben unbehandelt. Wie viel cm² Folie benötigt sie dafür mindestens?
Jule benötigt mindestens cm² Folie.
Versuche: 0
Aufgabe 23: Eine Schiffsschleuse ist 110 m lang und 12 m breit. Beim Schleusen eines Schiffes wird der Wasserspiegel um 6 m angehoben oder abgesenkt.
a) Wie viel Kubikmeter Wasser fließen beim Schleusen durch die Schleusenrohre? b) Um wie viel Meter ist der Wasserspiegel gesunken, wenn 5940 m³ Wasser aus der Schleuse abgelassen wurden? |
a) Beim Schleusen fließen m³ Wasser durch die Rohre. b) Der Wasserspiegel ist dann um m gesunken. |
Versuche: 0
Aufgabe 24: Ein Quader ist dreimal so lang wie hoch und doppelt so breit wie hoch. Seine Oberfläche ist 1078 cm² groß. Welches Volumen hat dieser Quader?
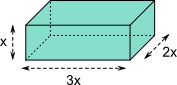
Der Quader hat ein Volumen von cm³.
Versuche: 0
Aufgabe 25: Die Wassermenge, die ein schwimmender Körper verdrängt, wiegt genausoviel, wie der Körper selbst. Man sagt dann, die Masse des Körpers ist gleich der Masse des verdrängten Wassers. Der Eiswürfle der Grafik wiegt als genausoviel wie das vorher im roten Bereich vorhandene Wasser. Eis hat eine Dichte von 0,9 g/cm³. Wasser hat eine Dichte von 1 g/cm³. Wie tief taucht ein Eiswürfel mit einer Kantenlänge von 3 cm ins Wasser ein?
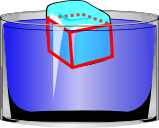
Ein Eiswürfel mit 3 cm Kantenlänge taucht cm ins Wasser ein.
Versuche: 0
Aufgabe 26: Ein Kupferwürfel mit einem Volumen von einem Kubikzentimeter wiegt 8,9 g. Wie dick (hoch) ist ein Kupferblech von 2 Metern Länge und 25 cm Breite, das 1,335 kg wiegt?
Das Kupferblech ist mm dick (hoch).
Versuche: 0