Lineare Gleichungssysteme
Zwei miteinander verknüpfte lineare Funktionen
Aufgabe 1: Ordne die Begriffe richtig zu.
- Haben zwei Geraden eine Steigung, dann haben sie einen klar definierten .
- Haben zwei Geraden die Steigung, aber einen y-Achsenabschnitt, liegen sie zueinander. Sie haben dann Schnittpunkt.
- Haben zwei Geraden die Steigung und den y-Achsenabschnitt, sind sie . Sie haben dann viele Schnittpunkte.
Versuche: 0
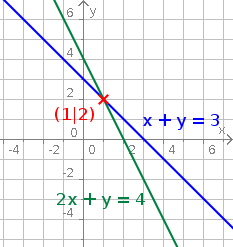Fügt man zwei lineare Funktionen mit je zwei Variablen (x|y) aneinander, dann spricht man von einem Gleichungssystem. Die Variablen, die gleichzeitig gültig in beiden Funktionen sind, gelten als Lösung des Gleichungssystems.
- Gleichung 1 (I) x + y = 3
- Gleichung 2 (II) 2x + y = 4
- Lösung: (1|2)
Lösung durch Wertetabelle
Einfache lineare Gleichungssysteme lassen sich durch das Anlegen von Wertetabellen lösen.
Jonas wechselt einen 10-Euro-Schein in x Ein-Euro-Münzen und y Zwei-Euro-Münzen. Insgesamt erhält er so 8 Geldstücke. Wie hat er gewechselt? Die Angaben lassen sich in zwei Gleichungen darstellen.
| 1 € · x + 2 € · y = 10 € | ||
| 1 · x + 2 · y = 10 | ||
| (I) | x + 2y = 10 | |
| x Münzen + y Münzen = 8 Münzen | ||
| (II) | x + y = 8 | |
Zur Lösung des Gleichungssystems kann man Zahlenpaare bilden, die das Ergebnis der jeweiligen Gleichung erzielen: |
||
| (I) | x + 2y = 10 | → (x|y); (0|5); (2|4); (4|3); (6|2); (8|1); (10|0) |
| (II) | x + y = 8 | → (x|y); (0|8); (1|7); (2|6); (3|5); (4|4); (5|3); (6|2); (7|1); (8|0) |
Das Zahlenpaar (6|2) kommt als einziges in beiden Gleichungen vor, daher ist es die Lösung: Jonas hat 6 Ein-Euro-Münzen und 2 Zwei-Euro-Münzen erhalten (10 € in 8 Münzen).
Aufgabe 2: Trage die Lösung des Gleichungssystems ein, das aus den folgenden Gleichungen besteht.
| (I) | x + 2y = 8 | → (-2|5); (0|4); (2|3); (4|2); (6|1); (8|0) |
| (II) | x + y = 6 | → (0|6); (1|5); (2|4); (3|3); (4|2); (5|1) |
| Lösung: | (|) |
Versuche: 0
Aufgabe 3: Ergänze die Wertetabelle und trage die Lösung ein.
| (I) | x - y = 3 | → (|0); (|1); (|2); (|3); (|4); (|5) |
| (II) | x - 2y = 1 | → (|0); (|1); (|2); (|3); (|4); (|5) |
| Lösung: | (|) |
Versuche: 0
Aufgabe 4: Ergänze die Wertetabelle und trage die Lösung ein.
| (I) | 2x - 3 = y | → (2|); (3|); (4|); (5|); (6|); (7|) |
| (II) | 3x = y + 9 | → (2|); (3|); (4|); (5|); (6|); (7|) |
| Lösung: | (|) |
Versuche: 0
Aufgabe 5: Ergänze die Wertetabelle und trage die Lösung ein.
| (I) | 2x +y = 16 | → (2|); 3|(); (4|); (5|); (6|); (7|) |
| (II) | x = 5y - 3 | → (|1); (|2); (|3); (|4); (|5); (|6) |
| Lösung: | (|) |
Versuche: 0
Aufgabe 6: Ergänze die Wertetabelle und trage die Lösung ein.
| (I) | y + x = 4 | → (x|y); (-4|); (-3|); (-2|); (-1|); (0|); (1|) |
| (II) | 2x + y = 1 | → (x|y); (-4|); (-3|); (-2|); (-1|); (0|); (1|) |
| Lösung: | (|) |
Versuche: 0
Lösung durch Zeichnung
Die Lösung eines linearen Gleichungssystems kann auch zeichnerisch ermittelt werden (s.u.).
Zur zeichnerischen Lösung eines Gleichungssystems werden zunächst beide Gleichungen auf die Form y = mx ± b gebracht..
(I) 1 y + 1 = x 3 → y = 3x - 3 (II) x + y = 5 → y = -x + 5 Danach werden die dazugehörigen Geraden in ein Koordinatensystem gezeichnet.
Der Schnittpunkt der beiden Geraden gibt die Lösungswerte an, die für beide Gleichungen gelten.
Lösung: (2|3)
Aufgabe 7: Ziehe die orangen Gleiter der Zeichnung so, dass die Geraden je eine Gleichung aus dem unteren Gleichungssystem widerspiegeln. Lies die entsprechenden Lösungswerte ab und trage sie unten ein. Tipp: Schiebe je einen Gleiter zur Konstante b auf der y-Achse.
| (I) (II) |
|
Lösung: (|)
richtig: 0falsch: 0
Aufgabe 8: Löse die Gleichungen nach y auf, zeichne die gesuchten Geraden in der Grafik von Aufgabe 7 und trage die Lösungen ein.
| a) | (I) 2x - y = -5 | → | y = x + | b) | (I) 3x + 4 y = -4 | → |
|
||||
| (II) 5x + y = -2 | → | y = x - | (II) x + 2y = 4 | → |
|
||||||
| Lösung: (|) | Lösung: (|) | ||||||||||
Versuche: 0
Sonderfälle
- Keine Lösung haben Gleichungssysteme, deren Gleichungen parallele Geraden erzeugen.
- Unendlich viele Lösungen haben Gleichungssysteme, deren Gleichungen übereinanderliegende Geraden erzeugen.
Aufgabe 9: Verändere die Position der orangen Gleiter und beobachte wie sich Gleichungen und Geraden anpassen. Ziehe die Geraden auch mal übereinander.
Lösung durch Rechnung
Der sicherste Weg zur Lösung eines linearen Gleichungssystems ist die Rechnung. In der Regel wird hierbei eines der folgenden Lösungsverfahren angewendet.
|
TB-Präsentation | Arbeitsblatt
|
TB-Präsentation | Arbeitsblatt
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sonderfälle
- Keine Lösung haben Gleichungssysteme, die zu falschen Aussagen führen.
(I) y
(II) y
5x + 2
2=
=
=
=5x + 2
5x + 3
5x + 3 | -5x
3 (falsch) - Unendlich viele Lösungen haben Gleichungssysteme, die zu allgemein gültigen Aussagen führen.
(I) y
(II) 2x - y
2x - (2x - 3)
2x - 2x + 3
3=
=
=
=
=2x - 3
3
3 | Ka
3
3
Aufgabe 10: Löse das Gleichungssystem.
Lösung: (|)
richtig: 0falsch: 0
Aufgabe 11: Löse das Gleichungssystem.
Lösung: (|)
richtig: 0falsch: 0
Aufgabe 12: Löse das Gleichungssystem.
Lösung: (|)
richtig: 0falsch: 0
Aufgabe 13: Vereinfache die Gleichungen und trage die Lösungen ein.
| a) | (I) 5× - 2y + 34 = 8x + y + 10 (II) 6x - 3y = 10x - 27 Lösung: (|) Versuche: 0 |
b) | (I) 6× + 5y - 10 = 2x + 7y (II) 2x + 6y + 7 = 6x + 7y - 6 Lösung: (|) Versuche: 0 |
Aufgabe 14: Vereinfache die Gleichung und trage die Lösung ein.
(II) 7x - 4y + 12 = 5y - 18
Lösung: (|)
Versuche: 0
Aufgabe 15: Löse das Gleichungssystem.
| (I) | |
| (II) |
Lösung: (|)
richtig: 0falsch: 0
Aufgabe 16: Trage die Koordinaten des Geradenschnittpunkts ein.
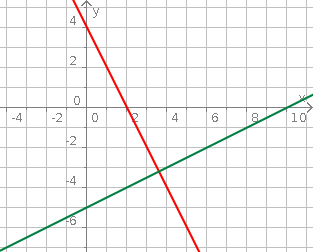
Lösung: (|)
Versuche: 0
Aufgabe 17: Trage die Koordinaten des Geradenschnittpunkts ein.
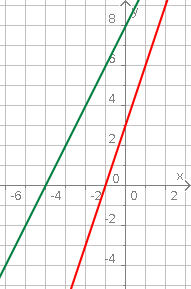
Lösung: (|)
Versuche: 0
Aufgabe 18: Trage die Koordinaten des Geradenschnittpunkts jeweils als Bruch mit Schrägstrich - z.B. S(8/9|-2/9) - ein. An den roten Markierungen kreuzen die Geraden exakt einen Gittereckpunkt.
S(|)
richtig: 0 ••••• falsch: 0
Aufgabe 19: Wenn einer von Leons Buntstiften (x) an Anna abgegeben wird, dann haben beide gleich viele Stifte vor sich auf dem Tisch liegen. Wird von Annas Buntstiften (y) einer zu Leon weitergereicht, dann hat er doppelt so viele Stifte vor sich liegen wie sie. Vervollständige die Rechnung und trage die Antwort ein.
Rechnung
|
(I) x
=
y
(II) (y ) = x |
Lösung: (|)
Versuche: 0
Aufgabe 20: Die Summe von x und y ist . Subtrahiert man x von y, dann erhält man . Wie groß sind die beiden Zahlen?
Antwort: x = ; y =
richtig: 0falsch: 0
Aufgabe 21: Die Summe zweier Zahlen ist . Die Zahl x ist um größer als die Zahl y. Wie groß sind beide Zahlen?
Antwort: x = ; y =
richtig: 0falsch: 0
Aufgabe 22: Das arithmetische Mittel (der Mittelwert) zweier Zahlen (x;y) beträgt . Subtrahiert man y von x, dann erhält man . Trage beide Zahlen ein.
Antwort: x = ; y =
richtig: 0falsch: 0
Aufgabe 23: Franz fährt mit einem Boot flussaufwärts mit einer mittleren Geschwindigkeit von km/h. Flussabwärts fährt er mit km/h. Wie groß ist die Eigengeschwindigkeit des Bootes und die Fließgeschwindigkeit des Flusses?.
Das Boot bewegt sich mit einer Eigengeschwindigkeit von km/h. Die Fließgeschwindigkeit beträgt km/h
richtig: 0falsch: 0
Aufgabe 24: Frau Egen und ihre Tochter sind zusammen 50 Jahre alt. Letztes Jahr war die Mutter genau dreimal so alt wie ihre Tochter. Wie alt sind die beiden heute?
Antwort: Frau Egen ist Jahre alt. Ihre Tochter Jahre.
Versuche: 0
Aufgabe 25: Bei einem Dreieck ist der Winkel α 8° größer als der Winkel γ und 35° kleiner als der Winkel β. Trage die Größen der jeweiligen Winkel ein.
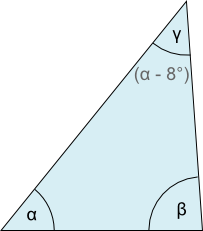
Antwort: Die Winkel haben folgende Größen: α = °; β = °; γ = °
Versuche: 0
Aufgabe 26: In einer Kleintierausstellung werden Wellensittiche und Kaninchen zur Schau gestellt. Alle Tiere zusammen haben Köpfe und Beine. Wie viele Kaninchen und wie viele Wellensittiche werden dort ausgestellt?
In der Ausstellung sind Kaninchen und Wellensittiche zu sehen.
richtig: 0falsch: 0
Aufgabe 27: In einer Jugendherberge gibt es Zimmer. In ihnen können 4 bzw. 6 Personen untergebracht werden. Insgesamt ist Platz für Personen. Wie viele Vierbett- und Sechsbettzimmer gibt es dort?
Die Herberge hat Vierbett- und Sechsbettzimmer.
richtig: 0falsch: 0
Aufgabe 28: Ben und Lisa haben Zimmer mit gleich großer Grundfläche. Bens Zimmer ist 50 cm länger als Lisas Zimmer. Dafür ist Lisas Zimmer 40 cm breiter als Bens Zimmer. Bens Zimmer ist 1,3 m länger als breit. Trage Länge und Breite von jedem Zimmer sowie ihren Flächeninhalt ein.
Antworten:
|
Versuche: 0
Aufgabe 29: Zwei Sorten Tee werden gemischt. Es sollen insgesamt 400 kg der Mischung hergestellt werden. Der Kilopreis der Sorte A beträgt 18 €. Sorte B erhält man für 22 €. Der Kilopreis für die Mischung soll 19,50 € betragen. Wie viel Kilogramm benötigt man von jeder Sorte?
Von Sorte A werden kg und von Sorte B kg hinzugefügt.
Versuche: 0
Aufgabe 30: Zwei Autofahrer wohnen 624 km voneinander entfernt und fahren einander entgegen. Wenn der erste um 7.00 Uhr losfährt und der zweite um 8.00 Uhr, dann treffen sie sich um 11.00 Uhr. Um diese Uhrzeit würden sie sich auch treffen, wenn der erste bereits um 5.00 Uhr und der zweite erst um 9.30 Uhr losfahren würde. Mit welcher Durchschnittsgeschwindigkeit sind die Fahrzeuge unterwegs gewesen?
Das schnelle Fahrzeug fuhr im Schnitt km/h und das langsame km/h.
Versuche: 0
Aufgabe 31: Archimedes sollte herausfinden, aus wie viel Gold- und Silberanteil die 10 kg schwere Krone des Königs von Syrakus bestand. Er wusste, das Gold im Wasser 1 19 und Silber 1 20 weniger zu wiegen schien. Nachdem er die Krone ins Wasser tauchte verlor sie anscheinend 0,625 kg. Das entsprach 1 16 ihres eigentlichen Gewichts. Wie viel Kilogramm Silber und wie viel Kilogramm Gold hätten sich unter dieser Voraussetzung rechnerisch in der Krone befinden müssen?
Rein rechnerisch hätten sich kg Gold und kg Silber in der Krone befunden. Das ... (Textvervollständigung nach der Auflösung.)
Versuche: 0