Zusammengesetzte Flächen
Einfache Flächen
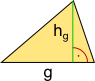
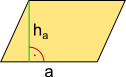
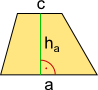
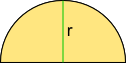
Aufgabe 1: Unten sind einige Flächen angegeben, in die sich zusammengesetzte Flächen zerlegen lassen. Klick jeweils den richtigen Namen und die dazugehörige Formel an.
| a) | ||||||||||||||||
|
|
|
|||||||||||||||
Versuche: 0
| b) | |||||||||||||||||
|
|
|
||||||||||||||||
Versuche: 0
| c) | |||||||||||||||
|
|
|
||||||||||||||
Versuche: 0
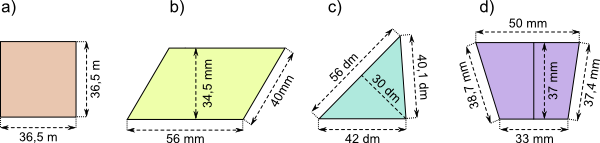
Aufgabe 2: Trage die Flächeninhalte der einfachen Flächen ein.
 |
|||
| a) A = m2 | b) A = mm2 | c) A = dm2 | d) A = mm2 |
Versuche: 0
Zusammengesetzte Flächen ohne Kreiselemente

Aufgabe 3: Klick zuerst im grauen Kasten auf eine einfache Fläche. Klick dann auf das Puzzlestück, an dessen Stelle die markierte einfache Fläche platziert sein muss, um die zusammengesetzte Fläche richtig zu füllen.





Aufgabe 4: Wähle eine Figur aus und stelle sie mit allen Tangramteilen nach.
|
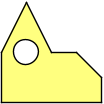
Aufgabe 5: Zusammengesetzte Flächen teilt man auf in einfache Flächen, deren Flächeninhalte dann addiert oder subtrahiert werden. Klick so lange auf die grünen Punkte, bis die richtigen Rechenzeichen angezeigt werden.
 |
|
 |
 |
Versuche: 0
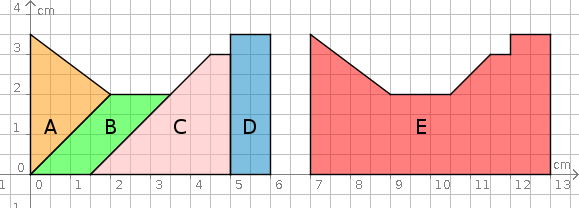
Aufgabe 6: Trage die Flächeninhalte der Flächen A-E ein.
 |
||||
| Dreieck A | Parallelogr. B | Trapez C | Rechteck D | Vieleck E |
| A = cm2 | A = cm2 | A = cm2 | A = cm2 | A = cm2 |
Versuche: 0
Aufgabe 7: Trage die Flächeninhalte der unteren Figuren richtig ein.
|
a) 
|
b) 
|
|
|
Die Figur hat einen Flächeninhalt von mm². |
Die Figur hat einen Flächeninhalt von cm². |
Versuche: 0
Aufgabe 8: Trage die Flächeninhalte der unteren Figuren richtig ein.
|
a) 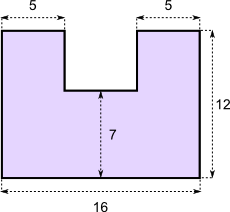
Angaben in cm |
b) 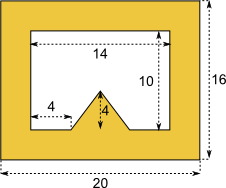
Angaben in cm |
|
|
Die Figur hat einen Flächeninhalt von cm². |
Die Figur hat einen Flächeninhalt von cm². |
Versuche: 0
Aufgabe 9: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 10: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 11: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 12: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 13: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 14: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 15: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 16: Trage die Flächeninhalte der unteren Figuren richtig ein.
|
a) 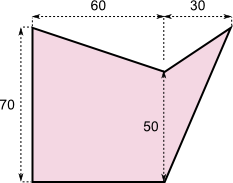
Angaben in cm |
b) 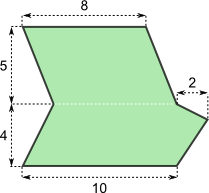
Angaben in cm |
|
|
Antwort a: Die Figur hat einen Flächeninhalt von cm2. |
Antwort b: Die Figur hat einen Flächeninhalt von cm2. |
Versuche: 0
Aufgabe 17: Übertrage die angegebenen Koordinaten in das Koordinatensystem und berechne den Flächeninhalt des Vielecks.
a) A(0|0); B(6|0); C(6|2); D(3|2); E(4|4); F(3|4); G(3|5); H(0|5)
b) A(1|0); B(6|0); C(7,5|1,5); D(7,5|3); E(6|4,5); F(6|5,5); G(2|5,5); H(2|3)
|
Antwort: Die Vielecke haben folgende Flächeninhalte:
a) cm2 |
Versuche: 0
Aufgabe 18: Die Seitenwand einer Fabrikhalle soll neu verputzt werden. Welche Kosten entstehen, wenn das Verputzen 90 € pro m² kostet?.
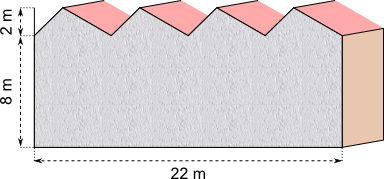
Antwort: Für das Verputzen der Seitenwand entstehen Kosten von €.
Versuche: 0
Aufgabe 19: Berechne die Fläche der Treppenhauswand (ohne Türen und Fenster).
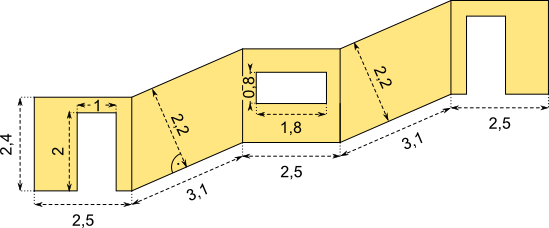
Angaben in Meter
Antwort: Das Treppenhaus hat eine Fläche von m².
Versuche: 0
Aufgabe 20: Trage den Flächeninhalt der grünen Fläche ein.
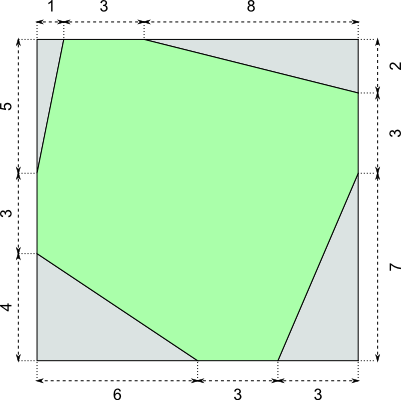
Antwort: Die grüne Fläche hat einen Flächeninhalt von cm2.
Versuche: 0
Aufgabe 21: Trage den Flächeninhalt des Sterns ein.
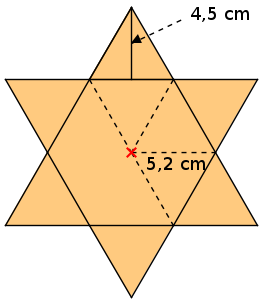
|
Der Stern hat einen Flächeninhalt von cm². Versuche: 0 |
Aufgabe 22: Trage die Flächeninhalte der unteren Figuren richtig ein.
|
a) 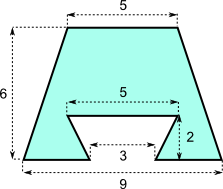
Angaben in cm |
b)
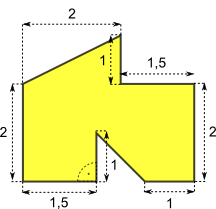
Angaben in cm |
|
|
Die Figur hat einen Flächeninhalt Versuche: 0 |
Die Figur hat einen Flächeninhalt Versuche: 0 |
Aufgabe 23: Trage den Flächeninhalt der Figuren ein.
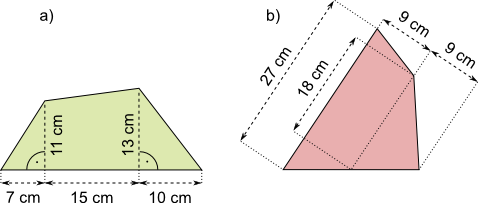
a) A = cm² b) A = cm²
Versuche: 0
Aufgabe 24: Färbe unten eine Fläche von cm² grün ein. (Jede Einheit stellt einen Zentimeter dar.)
|
richtig: 0 | falsch: 0 |
Zusammengesetzte Flächen mit Kreiselementen
Aufgabe 25: Berechne den Flächeninhalt der zusammengesetzten Fläche. Trage den fehlenden ganzzahligen Wert ein.
Die Figur hat einen Flächeninhalt von , cm2.
richtig: 0falsch: 0
Aufgabe 26: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein. Runde auf eine Nachkommastelle.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 27: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein. Runde auf eine Nachkommastelle.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 28: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein. Runde auf eine Nachkommastelle.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 29: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein. Runde auf eine Nachkommastelle.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 30: Berechne den Flächeninhalt der zusammengesetzten Fläche. Trage den fehlenden ganzzahligen Wert ein.
Die Figur hat einen Flächeninhalt von , cm2.
richtig: 0falsch: 0
Aufgabe 31: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein. Runde auf eine Nachkommastelle.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 32: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein. Runde auf eine Nachkommastelle.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 33: Miss mit Hilfe der beiden orange gestrichelten Lineale (rote Anfasser) die wichtigen Strecken, um den Flächeninhalt der zusammengesetzten Fläche zu ermitteln. Trage die Lösung unten ein. Runde auf eine Nachkommastelle.
Antwort: cm²
richtig: 0falsch: 0
Aufgabe 34: Die Ecken eines Quadrates berühren den Rand eines Kreises mit einem Radius von 4,5 cm. Welchen Flächeninhalt hat das Quadrat?
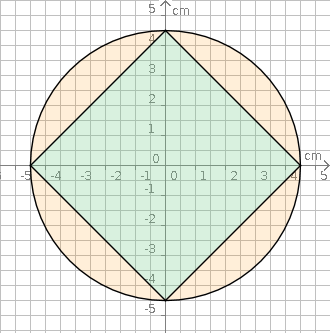
Das Quadrat hat einen Flächeninhalt von cm².
Versuche: 0
Aufgabe 35: Trage den Flächeninhalt der folgenden Figur ein. Runde auf eine Nachkommastelle.
Antwort: Die Figur hat einen Flächeninhalt von cm².
Versuche: 0
Aufgabe 36: Trage unten die fehlenden Ganzzahlen der Umfänge und der Flächeninhalte ein.
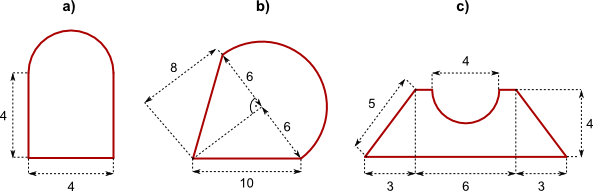 Angaben in cm |
|
|
a) Umfang von Figur: a) = ,3 cm b) = ,8 cm c) = ,3 cm Versuche: 0 |
b) Fläche von Figur: a) = ,3 cm2 b) = ,5 cm2 c) = ,7 cm2 Versuche: 0 |
Aufgabe 37: Trage die ganzzahligen Werte des Flächeninhalts der folgenden Messingstücke ein.
a)
|
b)
|
|
|
Das Messingstück hat eine Fläche Versuche: 0 |
Das Messingstück hat eine Fläche Versuche: 0 |
Aufgabe 38: Die gefärbten Bereich befindet sich je in einem Quadrat mit der Seitenlänge a = . Bestimme den roten Umfang und den Flächeninhalt der gefärbten Figur. Runde jeweils auf eine Nachkommastelle.
a) 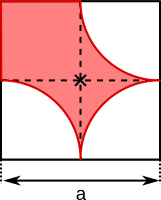 |
b) 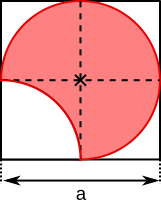 |
|
u = cm A = cm²
|
u = cm A = cm²
|
Aufgabe 39: Die Seite a ist cm lang. Trage den ganzzahligen Wert des Flächeninhaltes ein.

Der Flächeninhalt der Figur entspricht , cm²
richtig: 0falsch: 0
Aufgabe 40: Trage unten die fehlenden Ganzzahlen des Umfangs und des Flächeninhalts der folgenden Figuren ein.
|
a) 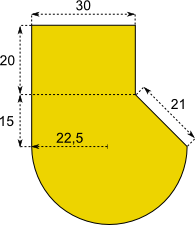
Angaben in cm |
b) 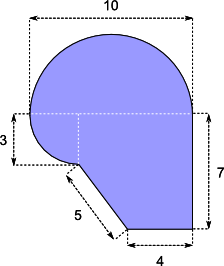
Angaben in cm |
|
|
u = ,7 cm A = ,7 cm² Versuche: 0 |
u = ,4 cm A = ,3 cm² Versuche: 0 |
Aufgabe 41: Trage unten die fehlenden Ganzzahlen des Flächeninhalts der folgenden Figuren ein.
|
a) 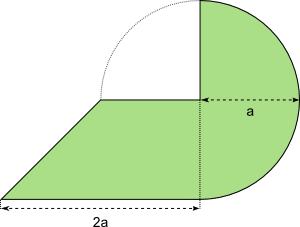
a = 2 cm |
b) 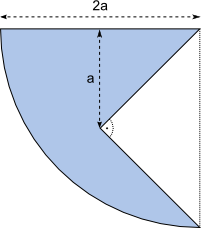
a = 5 cm |
|
|
A = ,3 cm² Versuche: 0 |
A = ,5 cm² Versuche: 0 |
Aufgabe 42: Trage den Flächeninhalt der Figuren ein. Runde auf ganze Quadratzentimeter.
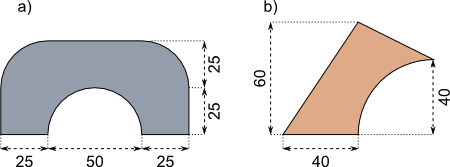
Angaben in cm
a) A = cm² b) A = cm²
Versuche: 0
Aufgabe 43: Berechne die orange Fläche (in cm²). Beachte dabei die Größe der Kästchen (unten links)! Runde auf eine Stelle nach dem Komma. Trage die Antwort ins untere Textfeld ein und überprüfe, ob du richtig gerechnet hast.
| Der Flächeninhalt beträgt cm²
|
Flächenberechnung mit dem Satz des Pythagoras
Aufgabe 44: Trage mithilfe des Satzes von Pythagoras den Flächeninhalt der folgenden Figur ein.

Antwort: Der Flächeninhalt beträgt cm².
Versuche: 0
Aufgabe 45: Trage mithilfe des Satzes von Pythagoras den Flächeninhalt der folgenden Figur ein.
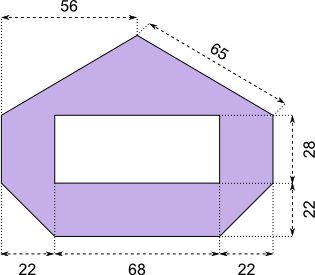
Angaben in cm
Antwort: Der Flächeninhalt beträgt cm².
Versuche: 0
Aufgabe 46: Gib mithilfe des Satzes von Pythagoras die Umfänge und die Flächeninhalte der Figuren an.
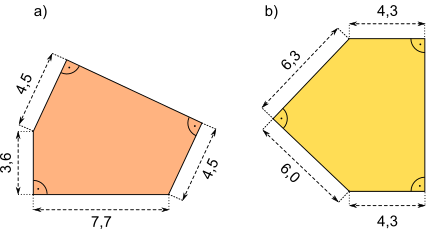
a) u = cm; A = cm² b) u = cm; A = cm²
Versuche: 0
Aufgabe 47: Gib mithilfe des Satzes von Pythagoras die Umfänge und die Flächeninhalte der Figuren an. Runde auf eine Nachkommastelle.
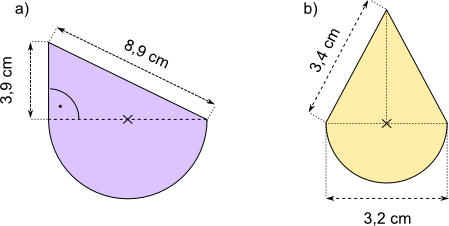
a) u = cm; A = cm² b) u = cm; A = cm²
Versuche: 0
Aufgabe 48: Bestimme den Umfang und den Flächeninhalt der gefärbten Fläche. Die Seite a = lang. Runde auf eine Nachkommastelle.
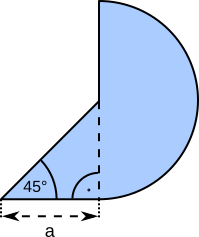
u = cm | A = cm²
richtig: 0falsch: 0
Aufgabe 49: Bestimme den Flächeninhalt der gefärbten Fläche. Die Seite a = lang. Runde auf eine Nachkommastelle.

A = cm²
richtig: 0falsch: 0
Aufgabe 50: Die Seite a = lang. Trage unten die Fläche des gelben Ringes ein. Runde das Ergebnis auf eine Nachkommastelle.
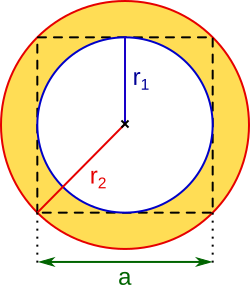
ARing = cm²
richtig: 0falsch: 0
Aufgabe 51: Berechne den Flächeninhalt. Trage die fehlenden ganzzahligen Werte ein (r = a).
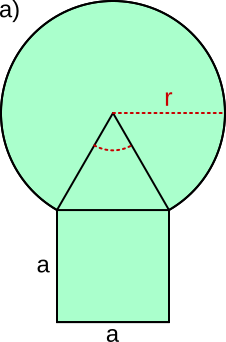 |
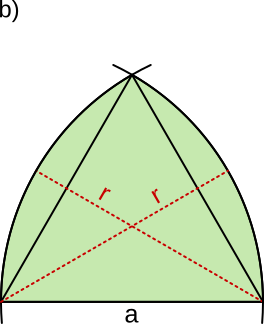 |
|
| r =
A = , cm2
|
← a = r → | r =
A = , cm2
|
Aufgabe 52: Gib mithilfe des Satzes von Pythagoras den Flächeninhalt der folgenden Figur an. Runde auf eine Nachkommastelle.

Das der Flächeninhalt beträgt cm².
Versuche: 0
Aufgabe 53: Das kleine blaue Quadrat hat einen Flächeninhalt von 2209 cm². Wie groß ist der Flächeninhalt des gesamten Quadrates, das rot umrandet ist?
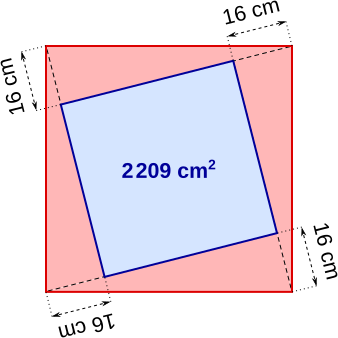
Der gesamte rot umrandeten Bereich hat einen Flächeninhalt von cm².
Versuche: 0
Aufgabe 54: Gib mithilfe des Satzes von Pythagoras den Flächeninhalt des folgenden Werkstücks an. Runde auf eine Nachkommastelle.
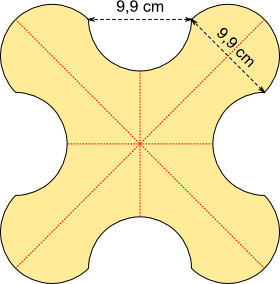
Das Werkstück hat einen Flächeninhalt von cm².
Versuche: 0
Aufgabe 55: Gib mithilfe des Satzes von Pythagoras den Flächeninhalt der folgenden Figur an.

Das der Flächeninhalt beträgt cm².
Versuche: 0
Aufgabe 56: Bei einem regelmäßigen, achtzackigen Stern bestehen die Zacken aus rechtwinkligen Dreiecken, die eine Kathetenlänge von jeweils 34 mm haben. Welchen Flächeninhalt hat der Stern? Runde auf ganze Quadratmillimeter.
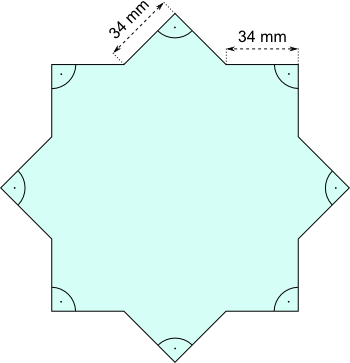
Das der Flächeninhalt beträgt mm².
Versuche: 0