Zehnerpotenzen

Aufgabe 1: Trage die richtigen Werte ein.

Auswertung

Versuche: 0

---

Aufgabe 2: Ziehe mit der Maus über die grauen Felder und betrachte, wie große Zahlen heißen, wie sie in Ziffern und als Zehnerpotent geschrieben werden.

Trillarden

Trillionen

Billiarden

Billionen

Milliarden

Millionen

Tausender

H

Z

E

H

Z

E

H

Z

E

H

Z

E

H

Z

E

H

Z

E

H

Z

E

H

Z

E

1

100

---

Aufgabe 3: Klick auf die Zehnerpotenz, deren Name in der Mitte angezeigt wird. Für 10 Versuche wird die Tabelle aus Aufgabe 2 unsichtbar.

Neu

0	1	2	3	4	5	6	7	8	9	10
25										11
24										12
23	22	21	20	19	18	17	16	15	14	13

richtig: 0 | falsch: 0

---

Aufgabe 4: Schreibe die Zahlen ausführlich. Und klick den richtigen Namen an.

Neu

a)	10	=	=   eins zehn einhundert eintausend zehntausend einhunderttausend eine Million zehn Millionen einhundert Millionen eine Milliarde
b)	10	=	=   eins zehn einhundert eintausend zehntausend einhunderttausend eine Million zehn Millionen einhundert Millionen eine Milliarde
c)	10	=	=   eins zehn einhundert eintausend zehntausend einhunderttausend eine Million zehn Millionen einhundert Millionen eine Milliarde
d)	10	=	=   eins zehn einhundert eintausend zehntausend einhunderttausend eine Million zehn Millionen einhundert Millionen eine Milliarde
e)	10	=	=   eins zehn einhundert eintausend zehntausend einhunderttausend eine Million zehn Millionen einhundert Millionen eine Milliarde
f)	10	=	=   eins zehn einhundert eintausend zehntausend einhunderttausend eine Million zehn Millionen einhundert Millionen eine Milliarde
g)	10	=	=   eins zehn einhundert eintausend zehntausend einhunderttausend eine Million zehn Millionen einhundert Millionen eine Milliarde
h)	10	=	=   eins zehn einhundert eintausend zehntausend einhunderttausend eine Million zehn Millionen einhundert Millionen eine Milliarde

Auswertung
richtig: 0 | falsch: 0

---

Aufgabe 5: Zerlege die Zahlen wie im Beispiel: 70 000 = 7 · 10 000

Neu

a) b) c)

Auswertung
richtig: 0falsch: 0

---

Aufgabe 6: Schreibe als Produkt mit Zehnerpotenz.

Neu
a)		=	· 10			b)		=	· 10
c)		=	· 10			d)		=	· 10
e)		=	· 10			f)		=	· 10
g)		=	· 10			h)		=	· 10
Auswertung richtig: 0 | falsch: 0

---

Aufgabe 7: Schreibe die Zahlen ausführlich.

Neu

a)	· 10	=
b)	· 10	=
c)	· 10	=
d)	· 10	=
e)	· 10	=
f)	· 10	=
g)	· 10	=
h)	· 10	=

Auswertung
richtig: 0falsch: 0

---

Aufgabe 8: Trage in das Textfeld eine große Zahl ein. Ziehe dann am Regler und betrachte, wie die Kommastelle des Faktors und der Exponent der Zehnerpotenz sich verändern. Klick anschließend unten den richtigen Wert an.

= 250000 · 10

0

Je kleiner der Faktor, desto größer kleiner die Zehnerpotenz.

Je größer der Faktor, desto größer kleiner die Zehnerpotenz.

Auswertung

Versuche: 0

---

Aufgabe 9: Trage die Oberflächendaten der jeweiligen Himmelskörper ausführlich ein (ohne Zehnerpotenzen).

Jupiter:	6,14 · 1010 km²	=  km²
Saturn:	4,26 · 1010 km²	=  km²
Uranus:	8,08 · 109 km²	=  km²
Neptun:	7,62 · 109 km²	=  km²
Erde:	5,1 · 108 km²	=  km²
Venus:	4,6 · 108 km²	=  km²
Mars:	1,45 · 108 km²	=  km²
Merkur:	7,48 · 107 km²	=  km²
Mond:	3,8 · 107 km²	=  km²

Auswertung

Versuche: 0

---

Aufgabe 10: Gib die Lösung als Ziffer-Wort-Kombination an. Die Ziffer trägst du ein und das Wort klickst du an. Du kannst unterschiedlichen Varianten wählen.

Beispiel
	4,3 21 · 1013
Bio.			Mrd.			Mio.			Tsd.
=	4	3	2	1	0	0	0	0	0	0	0	0	0	0
=	4	3	2	1	0	Milliarden
=	43 , 21				Billionen

Neu

a) =   Millionen Milliarden Billionen Billiarden b) =   Millionen Milliarden Billionen Billiarden c) =   Millionen Milliarden Billionen Billiarden

Auswertung
richtig: 0 | falsch: 0

---

Aufgabe 11: Klick auf die Ziffer, hinter der das Komma zu setzen ist.

Neu

a) = · 10 b) = · 10 c) = · 10 d) = · 10 e) = · 10

Auswertung
richtig: 0 | falsch: 0

---

Aufgabe 12: Klick unten auf die Werte, die in den roten Rahmen gehören.

a) 0,305 Millionen
b) 3,05 Millionen
c) 30,5 Millionen

30 500 000    0,305 ·10⁷    30,5 ·10⁶    305 000    0,305 ·10⁶    3,05 ·10⁶    3,05 ·10⁷    3 050 000    3,05 ·10⁵   

Auswertung
Versuche: 000

---

Aufgabe 13: Trage die fehlenden Werte ein.

Neu

· 10 = · 10 = · 10 = · 10 = · 10

Auswertung
richtig: 0falsch: 0

---

Aufgabe 14: Schreibe die Werte als Zahl, als Produkt und in wissenschaftlicher Schreibweise.

Neu

	Zahl	Produkt	Wissenschaftliche Schreibweise
a)			, · 10
b)		·	, · 10
c)		·
d)			, · 10

Auswertung
richtig: 0falsch: 0

---

Aufgabe 15: Schreibe die Zahlen in wissenschaftlicher Schreibweise.

Neu

a) = , · 10

b) 1200 = , · 10

c) 1200 = , · 10

d) 1200 = , · 10

Auswertung
richtig: 0falsch: 0

---

Neu

Aufgabe 16: Schreibe das Ergebnis von als Zehnerpotenz in wissenschaftlicher Schreibweise.

= , · 10

Auswertung
richtig: 0falsch: 0

---

Aufgabe 17: Schreibe die Zahlen ausführlich.

Neu

a)	10	=
b)	10	=
c)	10	=
d)	10	=
e)	10	=
f)	10	=
g)	10	=
h)	10	=

Auswertung
richtig: 0falsch: 0

---

Aufgabe 18: Schreibe die Zahlen ausführlich.

Neu

a)	· 10	=
b)	· 10	=
c)	· 10	=
d)	· 10	=
e)	· 10	=
f)	· 10	=
g)	· 10	=
h)	· 10	=

Auswertung
richtig: 0falsch: 0

---

Aufgabe 19: Trage in das Textfeld eine kleine Zahl ein. Ziehe dann am Regler und betrachte, wie die Kommastelle des Faktors und der Exponent der Zehnerpotenz sich verändern.

= 0,0025 · 10

0

Je größer der Faktor, desto größer kleiner die Zehnerpotenz.

Je kleiner der Faktor, desto größer kleiner die Zehnerpotenz.

Auswertung

Versuche: 0

---

Aufgabe 20: Trage die fehlenden Werte ein.

Neu

· 10 = · 10 = · 10 = · 10 = · 10

Auswertung
richtig: 0falsch: 0

---

Aufgabe 21: Schreibe als Zehnerpotenz.

Neu
a)		=	· 10			b)		=	· 10
c)		=	· 10			d)		=	· 10
e)		=	· 10			f)		=	· 10
g)		=	· 10			h)		=	· 10
Auswertung richtig: 0 | falsch: 0

---

Aufgabe 22: Finde eine Zahl, die zwischen den beiden aufgeführten Werten liegt und notiere sie als Zehnerpotenz.

Neu

a) < · 10 < b) < · 10 <

Auswertung
richtig: 0 | falsch: 0

---

Aufgabe 23: Schreibe als Zehnerpotenz.

Neu

a)	1	= 10		b)	1	=  · 10		c)	1	=  · 10
	10000				10000				10000

Auswertung
richtig: 0falsch: 0

---

Aufgabe 24: Schreibe als Bruch.

Neu

a)

10

=

1

b)

8 · 10

=

c)

· 10

5

=

Auswertung
richtig: 0falsch: 0

---

Aufgabe 25: Gib die Lösung als Ziffer-Wort-Kombination an. Die Ziffer trägst du ein und das Wort klickst du an.

Neu

a) =   Zehntel Hundertstel Tausendstel Millionstel b) =   Zehntel Hundertstel Tausendstel Millionstel c) =     Zehntel Hundertstel Tausendstel Millionstel

Auswertung
richtig: 0 | falsch: 0

---

Aufgabe 26: Wähle einen Aufgabentyp und gib die Lösung an.

Neu a) gleicher Exponent +- a) 10²=10 ·10 b) 5·10²=5·10·10 c) 10²=100 d) 5·10²=500 e) 500=5·10² f) 50 000=50 tausend a) 10-²=1:10·10 b) 5·10-²=5·1:10·10 c) 10-²=0,01 d) 5·10-²=0,05 e) 0,05=5·10-² f) 0,005=5 Tausendstel

Auswertung
richtig: 0 | falsch: 0

---

✎

Aufgabe 27: Trage die richtigen Werte ein.

Neu

Die Summe aus · 10 ³ und · 10 ² ist .

Die Differenz aus · 10 ³ und · 10 ² ist .

Auswertung
richtig: 0falsch: 0

---

✎

Aufgabe 28: Trage unten das Ergebnis der Rechnung richtig ein.

Neu

a) = · 10 b) = · 10 c) = · 10

Auswertung
richtig: 0 | falsch: 0

---

✎

Aufgabe 29: Trage den fehlenden Summanden als Zahl aus lauter Ziffern ein.

Neu

+ = + = + =

Auswertung richtig: 0falsch: 0

---

✎

Aufgabe 30: Starte ein Quiz und löse die Gleichungen.

jQuizMe-Quelle von: Larry Battle Lizenz: GPL

---

Aufgabe 31: Klick in der Liste die richtigen Zahlenwerte an.

Symbol	Name	Wert
Y	Yotta	1024	Quadrillion
Z	Zetta	1021	Trilliarde
E	Exa	1018	Trillion
P	Peta	1015	Billiarde
T	Tera	1012	Billion
G	Giga	109	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
M	Mega	106	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
k	Kilo	103	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
h	Hekto	102	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
da	Deka	101	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
—	—	100	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
d	Dezi	10-1	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
c	Zenti	10-2	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
m	Milli	10-3	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
μ	Mikro	10-6	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
n	Nano	10-9	eins hundert hundertstel Milliarde milliardstel Million millionstel tausend tausendstel zehn zehntel
p	Piko	10-12	billionstel
f	Femto	10-15	billiardstel
a	Atto	10-18	trillionstel
z	Zepto	10-21	trilliardstel
y	Yokto	10-24	quadrillionstel

Auswertung

Versuche: 0

---

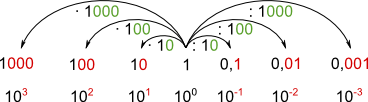Aufgabe 32: Trage in eines der unteren Textfelder eine Zahl ein und beobachte, wie diese Zahl in anderen Einheiten als Zehnerpotenz geschrieben wird. Achte auf die Position des Kommas und den Wert des Exponenten.

		Zahl		Zehnerpotenz	Komma- verschiebung	Exponent- änderung
Kilo				a
Hekto				a
Deka				a
B g HZ J l m Pa V				a
Dezi				a
Zenti				a
Milli				a

---

Aufgabe 33: Trage in eines der unteren Textfelder eine Zahl ein und beobachte, wie diese Zahl in anderen Einheiten als Zehnerpotenz geschrieben wird. Die Zeile darunter zeigt einen vor dem Komma einstelligen Vergleichswert an.

km	=	m	=	dm	=	cm	=	mm
	=		=		=		=

---

Aufgabe 34: Für die Bezeichnung großer Zahlen verwendet man oft die Begriffe Kilo, Mega, Giga.

• 1 Kilotonne = 1 kt = 1000 t
• 1 Megatonne = 1 Mt = 1000 kt
• 1 Gigatonne = 1 Gt = 1000 Mt

Ergänze die jeweilige Zehnerpotenz bei der Umwandlung in Tonnen (t).

a) 1 kt = 10 t; b) 1 Mt = 10 t; c) 1 Gt = 10 t

Auswertung

Versuche: 0

---

Aufgabe 35: Im Klappmenü kannst du erkennen, welche Vorsilben bestimmter Maßeinheiten welchen Wert haben. Notiere die aufgeführten Werte in ihrer Grundeinheit als Zehnerpotenz.

Giga → 1 000 000 000 Mega → 1 000 000 Kilo → 1 000 Hekto → 100 Deka → 10 Dezi → 0,1 Zenti → 0,01 Milli → 0,001
a) 1 Kilometer (km) = 10 m	f) 1 Megavolt (MV) = 10 V
b) 1 Hektopascal (hPa) = 10 Pa	g) 1 Millimeter (mm) = 10 m
c) 1 Kilojoule (KJ) = 10 J	h) 1 Deziliter (dl) = 10 l
d) 1 Gigabyte (GB) = 10 B	i) 1 Dezitonne (dt) = 10 t
e) 1 Hektoliter (hl) = 10 l	j) 1 Megahertz (MHZ) = 10 HZ

Auswertung

Versuche: 0

---

Aufgabe 36: Notiere die aufgeführten Werte in ihrer Grundeinheit als Zehnerpotenz.

Neu
a) 1 Kilometer (km) = 10 m	f) 1 Megavolt (MV) = 10 V
b) 1 Hektopascal (hPa) = 10 Pa	g) 1 Millimeter (mm) = 10 m
c) 1 Kilojoule (KJ) = 10 J	h) 1 Deziliter (dl) = 10 l
d) 1 Gigabyte (GB) = 10 B	i) 1 Dezitonne (dt) = 10 t
e) 1 Hektoliter (hl) = 10 l	j) 1 Megahertz (MHZ) = 10 HZ
Auswertung richtig: 0falsch: 0

---

Aufgabe 37: Schreibe die Längen in m. Benutze dazu Zehnerpotenzen.

a) 1 mm = 10 m	d) 0,067 dm = 6,7 · 10 m
b) 0,003 mm = 3 · 10 m	e) 0,0083 m = 8,3 · 10 m
c) 45 mm = 4,5 · 10 m	f) 0,0647 cm = 6,47 · 10 m
Auswertung Versuche: 0

---

Aufgabe 38: Wandle folgende in der Physik gebräuchliche Längeneinheiten in Zehnerpotenzen eines Meters um.

a)	1 Mikrometer (1 µm) 1 µm =  1  mm = 10 m 1 000
b)	1 Nanometer (1 nm) 1 nm =  1  mm = 10 m 1 000 000
c)	1 Picometer (1 pm) 1 pm =  1  mm = 10 m 1 000 000 000
Auswertung Versuche: 0

---

Aufgabe 39: Die Wellenlänge des sichtbaren Lichts liegt zwischen 0,00000038 m und 0,00000075 m, die der Röntgenstrahlen zwischen 0,000000000006 m und 0,00000001 m. Schreibe diese Wellenlängen als Zehnerpotenz und gib sie in Nanometer (nm) und Picometer (pm) an.

Antwort

• Wellenlänge des Lichts: von 3,8 · 10 m bis 7,5 · 10 m →  nm bis  nm

• Wellenlänge der Röntgenstrahlen: von 6 · 10 m bis 10 m → pm bis pm

Auswertung

Versuche: 0

---

Aufgabe 40: Trage unten die richtigen Zahlen ein.

Analysewaagen wiegen in der Regel auf 0,1 Milligramm (mg) genau. Wie wird diese Genauigkeit in Gramm (g) und Kilogramm (kg) dargestellt?

Antwort:

1. 0,1 mg = 10 g
2. 0,1 mg = 10 kg

Mikrowaagen sind noch exakter und können auf ein tausendstel Milligramm, also ein Mikrogramm (µg) genau messen. Stelle die Genauigkeit dieser Waagen in Milligramm, Gramm und Kilogramm dar.

Antwort:

1. 1 µg = 10 mg
2. 1 µg = 10 g
3. 1 µg = 10 kg

Auswertung

Versuche: 0

---

✎

Aufgabe 41: Ein Spinnenfaden kann einen Durchmesser von nur 5 · 10-3 mm aufweisen. In einem Buch über Spinnen wird er mit 1 500-facher Vergrößerung abgebildet. Wie groß ist der Durchmesser dieses Fadens auf der Abbildung? Antwort: Der Faden der Spinne hat auf der Abbildung einen Durchmesser von  mm. Auswertung Versuche: 0

---

✎

Aufgabe 42: Das Herz einer Maus schlägt durchschnittlich 500 Mal pro Minute. Wie oft schlägt das Mäuseherz im Jahr?

Antwort: Es schlägt , · 10 Mal in einem Jahr.

Auswertung

Versuche: 0

---

✎

Aufgabe 43: Trage unten die richtigen Zahlen ein.

Blonde Menschen haben durchschnittlich 150 000 Haare auf dem Kopf. Bei Schwarzhaarigen sind es 110 000, bei Brünetten 100 000 und bei Rothaarigen 75 000. Täglich wächst jedes Haar ungefähr 0,4 mm. Wie viel Meter Haare produzieren die unterschiedliche Typen täglich?

Antwort: Die verschiedenen Haartypen produzieren durchschnittlich so viel Meter Haar:

1. Blondhaarige:  m
2. Schwarzhaarige:  m
3. Brünette:  m
4. Rothaarige:  

Auswertung

Versuche: 0

---

Aufgabe 44: Im Nordseewatt leben im Schnitt 40 Wattwürmer je Quadratmeter. Jeder einzelne Wattwurm filtert im Laufe eines Jahres 25 kg Sand. Den gereinigten Sand scheidet er als spaghettiartige Häufchen aus (siehe Bild). a)  Wieviel Sand wird von den Wattwürmern auf einer Wattfläche von einem Kilometer Länge und hundert Metern Breite jedes Jahr gereinigt? b)  Wie viele 3-achsige Sattelzüge (LKW) mit einer Zuladung von 25 Tonnen würden benötigt, um den auf dieser Fläche gefilterte Menge Sand abzutransportieren? a)  Auf dieser Fläche reinigen die Wattwürmer jedes Jahr 10 kg Sand. b)  Zum Abtransport dieser Menge Sand benötigte man Sattelzüge. Auswertung Versuche: 0

✎ Wattwurm haufen von: M.Buschmann Lizenz: Public Domain Original: Hier

Der gesamte Sand des Nordseewatts bis 20 Zentimeter Tiefe wird vom Wattwurm innerhalb eines Jahres gefressen und wieder ausgeschieden.

---

✎

Aufgabe 45: Ein Bleiatom wiegt 3,44 · 10^-22 Gramm. Wie viele Bleiatome befinden sich in einem Kilogramm Blei? Kürze den Faktor vor der Zehnerpotenz auf 3 Nachkommastellen.

Es befinden sich , · 10 Atome in einem Kilogramm Blei.

Auswertung

Versuche: 0

---

✎

Aufgabe 46: Eine Brücke ist 650 m lang. Jeder Meter dieser Brücke dehnt sich bei einer Temperaturerhöhung von einem Grad um 1,2 · 10^-5 m aus. Um wie viel cm ist die Brücke im Sommer bei 50° C länger als im Winter bei -20° C?

Antwort: Die Brücke ist im Sommer  cm länger als im Winter.

Auswertung

Versuche: 0

---

✎

Aufgabe 47:	Die Erde hat ein Gewicht von etwa 5,97 · 1024 kg. Die Sonne wiegt ca. 1,99 · 1030 kg.
	a)	Wie viel Mal schwerer ist die Sonne im Vergleich zur Erde? Runde auf Tausender.
	b)	Wie viel Gigatonnen wiegt die Erde?
Antwort:	a)	Die Sonne wiegt 000 Mal mehr als die Erde.
	b)	Die Erde wiegt 5,97 · 10Gigatonnen.

Auswertung

Versuche: 0

---

✎

Aufgabe 48: Lenas Hund "Snoopy" ist genau 10 Jahre alt. Seit wie vielen Sekunden ist er bereits auf der Welt? (Rechne mit 365 Tagen pro Jahr.)

Snoopy lebt seit , · 10 Sekunden.

Auswertung

Versuche: 0

---

✎

Aufgabe 49: Trage unten die richtigen Zahlen ein. Achte auf die Einheiten.

Eine 100-€-Banknote ist 9 · 10^-3 cm dick. Wie hoch ist ein Stapel 100-€-Scheine im Wert von:

1. 1 Mio. Euro?
   Antwort:  cm
2. 1 Mrd. Euro?
   Antwort:  m
3. Deutschlands Schulden 2011 von etwa 2000 Mrd. Euro?
   Antwort:  km

Auswertung

Versuche: 0

---

Aufgabe 50: Das Bild "Salvator Mundi" von "Leonardo da Vinci" wurde 2017 für 4,503 · 10⁸ $ verkauft. Wie viele Jahre müsste jemand sparen, der 25 000 $ im Monat zurücklegen könnte (Zinsen werden nicht berücksichtigt), um das Gemälde zu kaufen. Schätze zuerst, bevor du rechnest.

Der Bildliebhaber müsste Jahre lang jeden Monat 25 000 $ sparen, um das Bild kaufen zu können.

Auswertung

Versuche: 0

---

✎

Aufgabe 51: Die Sonden Helius 1 und Helius 2 bewegten sich mit einer Geschwindigkeit von 250 000 km/h durch das Weltall. Wie viele Jahre - rechne mit 365 Tagen pro Jahr - wäre ein Flugkörper mit diesem Tempo unterwegs, wenn er auf direktem Weg zum 4,3 Lichtjahre entfernten, nächsten Fixstern, "Alpha Centauri", fliegen könnte? Ein Lichtjahr entspricht 9,46 · 10¹² km. Runde auf ganze Jahre.

Der Flugkörper bräuchte Jahre, um nach Alpha Centauri zu kommen.

Auswertung

Versuche: 0

---

✎

Aufgabe 52: Ein Armreif mit einer Oberfläche von 12 cm² wird mit einer 2 · 10^-3 mm starken Legierung von 18 Karat Rotgold beschichtet. Das Rotgold hat einen Preis von 35 €/g und ein Gewicht von 15 g/cm³. Wie hoch ist der Materialpreis des Goldes?

Das verwendete Rotgold kostet €.

Auswertung

Versuche: 0

---