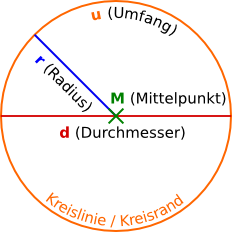
Aufgabe 1: Klick jeweils den Begriff an, der in den roten Rahmen gehört.
|
d
Durchmesser
Mittelpunkt
r
Radius
Umfang
|
Aufgabe 2: Klick auf die Zahlen und trage die gesuchten Begriffe ein.
|
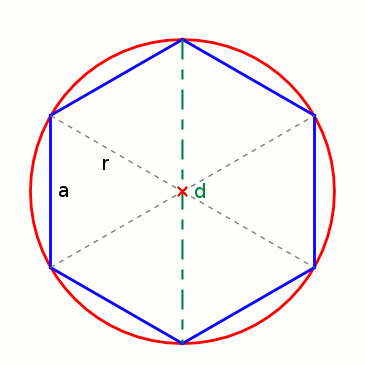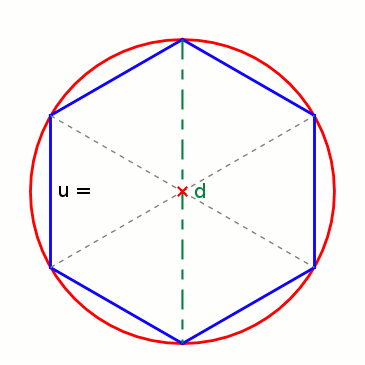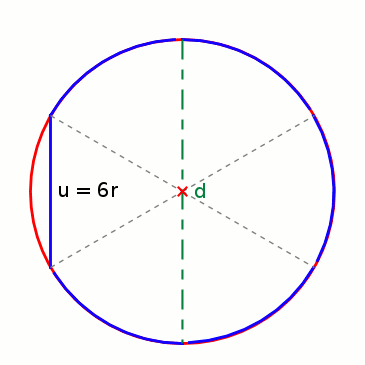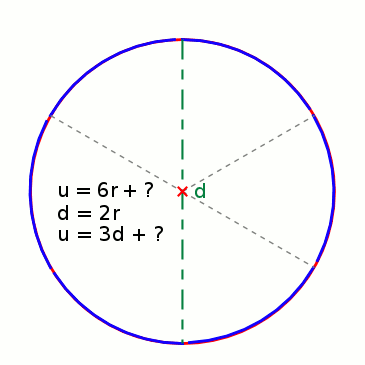
Ungefähre Umfangbestimmung
Aus 6 Radien (r) können die Seiten (a) eines Sechsecks gebildet werden, das genau in einen Kreis mit entsprechendem Radius hineinpasst. Werden die Seiten an den Kreisumfang angepasst, bleibt jeweils ein kleiner Rest, um den Umfang ganz schließen zu können. Der Umfang eines Kreises ist also so lang wie 3 Mal der Durchmesser (6 · r) plus einem Rest. Wie groß aber ist dieser Rest genau?
Kreiszahl Pi (π = 3,141592...)
Die Kreiszahl π gibt das Verhältnis zwischen dem dem Umfang (u) und Durchmesser (d) eines Kreises an. Für jeden Kreis gilt, dass sein Durchmesser genau π mal in seinen Umfang passt.
Aufgabe 3: Rolle mit dem orangen Gleiter unterschiedlich große Kreise ab und klicke anschließend unten die Daten die jeweils in das rote Kästchen gehören.
|
Merke:
Der Kreisdurchmesser passt genau , ...
Mal in den Kreisumfang hinein. Die Kreiszahl π ist , ... Umfangformel: = · π
1
1
3
3
4
4
d
u
|
Aufgabe 4:
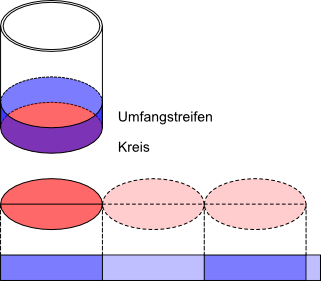
- Zeichne die Bodenfläche eines zylindrischen Glases (einen Kreis) auf ein Stück Pappe.
- Knick den Pappkreis hälftig (Durchmesser).
- Lege eine Pappstreifen um das Glas herum und schneide ihn auf Umfanglänge ab.
- Wie viele Durchmesser des Kreises kannst du auf den Umfangstreifen aneinanderreihen?
Formeln
Folgende Formeln spielen bei der Umfangberechnung eine wichtige Rolle:
| Umfang | u = d · π | |||||
| u = 2 · r · π | → | u = 2r · π | ||||
| Durchmesser | d = u : π | → |
|
|||
| Radius | r = u : π : 2 | → |
|
Aufgabe 5: Trage die richtigen Kreisumfänge ein. Runde das Ergebnis auf eine Nachkommastelle.
a) cm | b) cm | c) cm
richtig: 0falsch: 0
Aufgabe 6: Trage die richtigen Kreisumfänge ein. Das Ergebnis ist auf eine Nachkommastelle gerundet.
| d |
u |
|
d |
u |
|
d |
u |
| a) 1 cm |
,14 cm |
d) 10 cm |
,4 cm |
g) 100 cm |
,2 cm |
||
| b) 2 cm |
,28 cm |
e) 20 cm |
,8 cm |
h) 200 cm |
,3 cm |
||
| c) 3 cm |
,42 cm |
f) 30 cm |
,2 cm |
i) 300 cm |
,5 cm |
Versuche: 0
Aufgabe 7: Trage die richtigen Durchmesser ein. Runde auf ganze Zentimeter.
| u |
d |
|
u |
d |
|
u |
d |
| a) 25,1 cm |
cm |
d) 44 cm |
cm |
g) 84,8 cm |
cm |
||
| b) 15,7 cm |
cm |
e) 56,5 cm |
cm |
h) 100,5 cm |
cm |
||
| c) 28,3 cm |
cm |
f) 66 cm |
cm |
i) 125,6 cm |
cm |
Versuche: 0
Aufgabe 8: Trage die ganzen Zahlen der Kreisdaten ein. Die gerundete Nachkommastelle ist vorgegeben!
| r | d | u | |
| a) | cm | cm | ,0 cm |
| b) | cm | cm | ,2 cm |
| c) | cm | cm | cm |
richtig: 0falsch:
0
Aufgabe 9: Du siehst einen Ausschnitt aus dem Plan eines Fußballfeldes. Welchen Umfang hat der Anstoßkreis?.
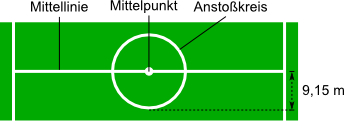
Der Anstoßkreis hat einen Umfang von ,5 m.
Versuche: 0
Aufgabe 10: Klick unten auf den "AUTO"-Button und schau dir an, wie man Umfänge von Teilkreisen berechnet.
© 2000 - http://geonext.de
 |
|||||
|
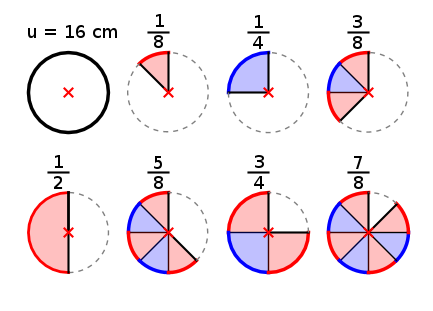
Aufgabe 11: Die Bogenlänge eines Teilkreises berechnet man, indem die Bogenlängen möglicher Kreisteile ermittelt werden. Trage in die unteren Textfelder die Bogenlänge der entsprechenden Teilkreise ein, wenn der Umfang des Vollkreises 16 cm beträgt.
|
|||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|||||||
Versuche: 0
Aufgabe 12: Trage die richtigen Werte der orangen Kreisbögen ein. Die gerundete Nachkommastelle ist vorgegeben!
|
|
||
| Sektor | Bogenlänge | |
| a) | , cm | |
| b) | , cm | |
| c) | , cm | |
| d) | , cm | |
| e) | , cm | |
richtig: 0falsch: 0
Aufgabe 13: Trage die richtigen Werte der Umfänge der Figuren ein. Die gerundete Nachkommastelle ist vorgegeben!
|
|
||
| Figur | Umfang | |
| a) | , cm | |
| b) | , cm | |
| c) | , cm | |
| d) | , cm | |
| e) | , cm | |
richtig: 0falsch: 0
Aufgabe 14: Trage die Umfänge der Figuren ein.
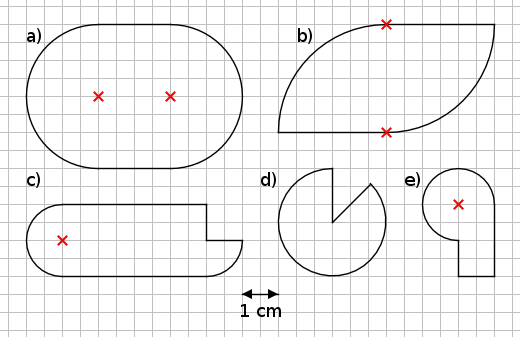
Die Figuren haben folgende Umfänge:
a) = ,6 cm | b) = ,4 cm | c) = ,7 cm
d) = ,2 cm | e = ,7 cm
Versuche: 0
Aufgabe 15: Trage den Umfang der folgenden Figur ein.
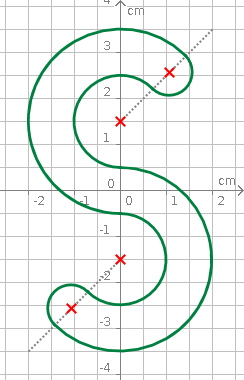
Das "S" hat einen Umfang von ,7 cm.
Versuche: 0
Aufgabe 16: Trage die richtigen Umfänge der grünen Figuren ein. Die gerundete Nachkommastelle ist vorgegeben!
| Figur | Umfang (u) |
| a) | , cm |
| b) | , cm |
| c) | , cm |
| d) | , cm |
richtig: 0falsch: 0
Aufgabe 17: Trage den Umfang der Figur unten ein. Runde auf eine Nachkommastelle.
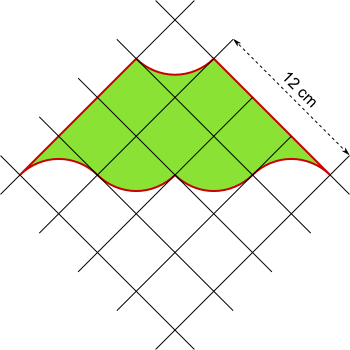
Der Umfang beträgt cm.
Versuche: 0
Aufgabe 18: Die folgende Spirale besteht aus 8 Viertelkreisen. Trage den Umfang der Spirale unten ein.
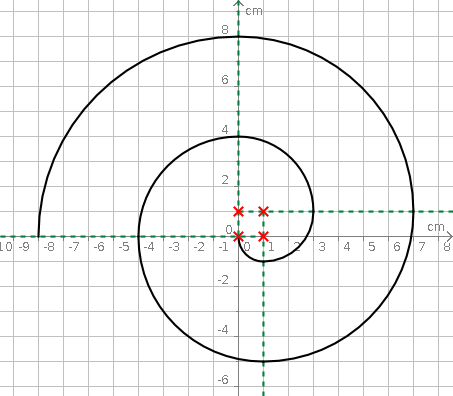
Die Spirale hat einen Umfang von ,5 cm.
Versuche: 0
Aufgabe 19: Trage den Umfang der Figur unten ein. Runde auf ganze Zentimeter.
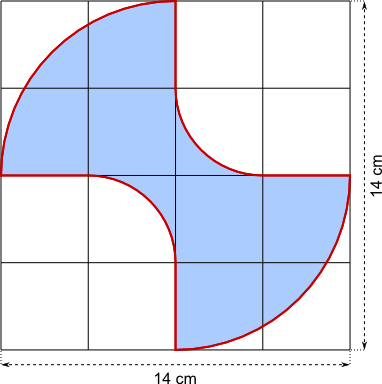
Der Umfang beträgt cm.
Versuche: 0
Aufgabe 20: Trage den Umfang der dargestellten "2" unten ein.
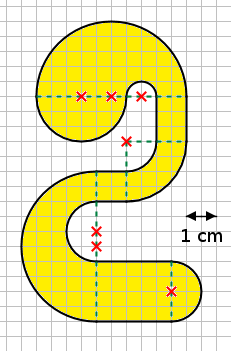
Die dargestellte "2" hat einen Umfang von ,0cm.
Versuche: 0
Aufgabe 21: Ziehe die beiden orangen Punkte der Grafik und beobachte die stattfindenden Veränderungen. Klick anschließend so auf die unteren Begriffe, dass der Satz richtig zusammengefügt wird.
|
Die Umfänge
genauso groß wie
sind zusammengenommen immer
des blauen und des
orangen Kreises.
grünen Kreises
der Umfang des
|
Versuche: 0
Aufgabe 22: Trage den ganzzahligen Umfang jeder Figur unten ein.
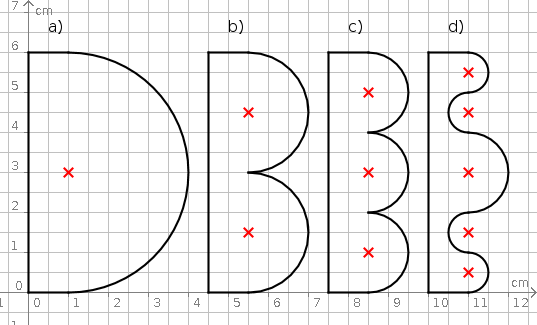
Die Figuren haben folgende Umfänge:
a) = ,4 cm | b) = ,4 cm | c) = ,4 cm | d) = ,4 cm
Versuche: 0
Aufgabe 23: Kreis a hat einen Umfang von 100 cm. Der Umfang von Kreis b ist 44 cm größer, also 144 cm. Kreis c hat ebenfalls einen 44 cm größeren Umfang (188 cm) als der vorhergehende Kreis. Trage ein, wie viel cm der Durchmesser der nachfolgenden Kreise jeweils größer ist. Runde auf ganze cm.
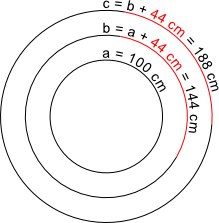
Der Durchmesser von Kreis b ist cm größer als der Durchmesser von Kreis a. Der Durchmesser von Kreis c ist cm größer als der Durchmesser von Kreis b. |
Versuche: 0
Aufgabe 24: Ein kreisrundes Steinkunstwerk mit einem Umfang von 10 m ist gleichmäßig von einer 44 cm längeren Kupferschiene (10,44 m) umrahmt. Wie groß ist der Abstand zwischen Stein und Schiene? Runde auf ganze cm.
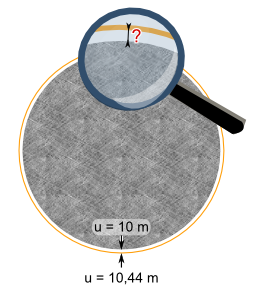
Die Schiene läuft in einem Abstand von cm um den Stein herum.
Versuche: 0
Aufgabe 25: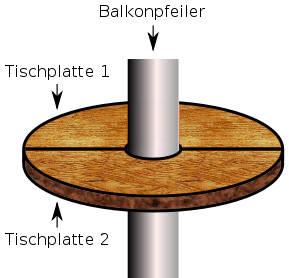 
Ein Schreiner soll aus zwei halbkreisförmigen Holzplatten einen Tisch erstellen, der an einem Balkonpfeiler zu befestigen ist. Der Pfeiler hat einen Umfang von cm. Welchen Radius hat das Loch des Tisches? Trage den ganzzahligen Radius unten ein.
Das Loch hat einen Radius von cm.
Versuche: 0
Aufgabe 26: Die vordere Scheibe eines Riehmenantriebs hat einen Radius von 12 cm. Wie oft dreht sich die hintere Scheibe bei einem Radius von 6, 4 oder 3 cm um sich selbst, wenn die vordere Scheibe eine Umdrehung gemacht hat?
|
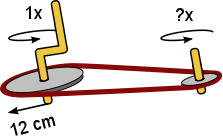
Radius
vorn |
Radius
hinten |
Umdrehungen
hinten |
| 12
cm |
6 cm | ||
| 4 cm | |||
| 3 cm |
Versuche: 0
Aufgabe 27: Die Größe von Fahrrädern wird in der bei uns veralteten Längeneinheit Zoll angegeben. 1 Zoll entspricht 2,54 cm. Trage unten ein, welchen Durchmesser und welchen Umfang die für die entsprechende Altersangabe empfohlenen Kinderräder haben.
| Kinderfahrrad Größenempfehlung | |||
| Alter bei normaler Körpergröße |
Radgröße in Zoll |
Durchmesser in cm |
Umfang in cm |
| 2 - 4 Jahre | 12 Zoll | ,48 | ,8 |
| 4 - 5 Jahre | 16 Zoll | ,64 | ,7 |
| 5 - 6 Jahre | 18 Zoll | ,72 | ,6 |
| 6 - 8 Jahre | 20 Zoll | ,80 | ,6 |
| 8 - 10 Jahre | 24 Zoll | ,96 | ,5 |
Versuche: 0
Aufgabe 28: Hochräder haben unterschiedliche Raddurchmesser. Welche Strecke legen Hochräder mit folgenden Raddurchmessern zurück, wenn sie 10 Umdrehungen gemacht haben? Trage die fehlenden Meter-Werte ein.
|
Raddurchmesser | zurückgelegte Strecke nach 10 Umdrehungen |
| 1,10 m | ,56 m | |
| 1,20 m | ,70 m | |
| 1,30 m | ,84 m | |
| 1,40 m | ,98 m | |
| 1,50 m | ,12 m | |
|
Fotothek df pk 0000316 027
Pfingsten 1947.jpg
von: Deutsche Fotothek Lizenz: CC BY-SA 3.0 Original: Hier |
||
Versuche: 0
|
Aufgabe 29: Die Turmuhr des Elizabeth Towers (Big Ben) hat ein Zifferblatt mit einem Durchmesser von 7 m. Welche Strecke legt die Spitze des Minutenzeigers, die sich genau entlang des Zifferblattrandes bewegt, in einer Stunde, an einem Tag und in einem Jahr zurück? Runde auf ganze Meter (Kilometer).
Versuche: 0 |
|
Aufgabe 30: In einer verbesserten Version des Patent-Motorwagen Nummer 1 absolvierte Bertha Benz 1888 die erste Fernfahrt der Automobilgeschichte. Sie fuhr über Umwege von Mannheim nach Pforzheim und zurück. Dabei überwand sie eine Strecke von 180 km. Das Vorderrad hatte einen Durchmesser von 730 mm, der Durchmesser der Hinterräder betrug je 1125 mm. Wie viele Umdrehungen machte auf dieser Strecke das Vorderrad und wie oft drehten sich die Hinterräder um sich selbst? Runde auf 1000er.
|
|
Versuche: 0
Aufgabe 31: Krümel schafft in 7 Sekunden 12 Runden in seinem Hamsterrad. Das Rad hat einen inneren Durchmesser von 25 cm. Mit welcher Geschwindigkeit (km/h) bewegt sich Krümel im Schnitt? Runde auf eine Nachkommastelle.
Krümel bewegt sich mit einer Geschwindigkeit von km/h.
Versuche: 0
Aufgabe 32: Windräder vom Typ E-126 haben einen Rotordurchmesser von 127 m und eine variable Drehzahl von 5 - 11,7 Umdrehungen pro Minute. Mit wie viel km/h bewegen sich die äußeren Rotorspitzen bei minimaler und bei maximaler Drehzahl? Runde auf ganze km/h.
Die Rotorspitzen haben bei 5 U/min ein Tempo von km/h. Bei 11,7 U/min bewegen sie sich mit einer Geschwindigkeit von km/h.
Versuche: 0